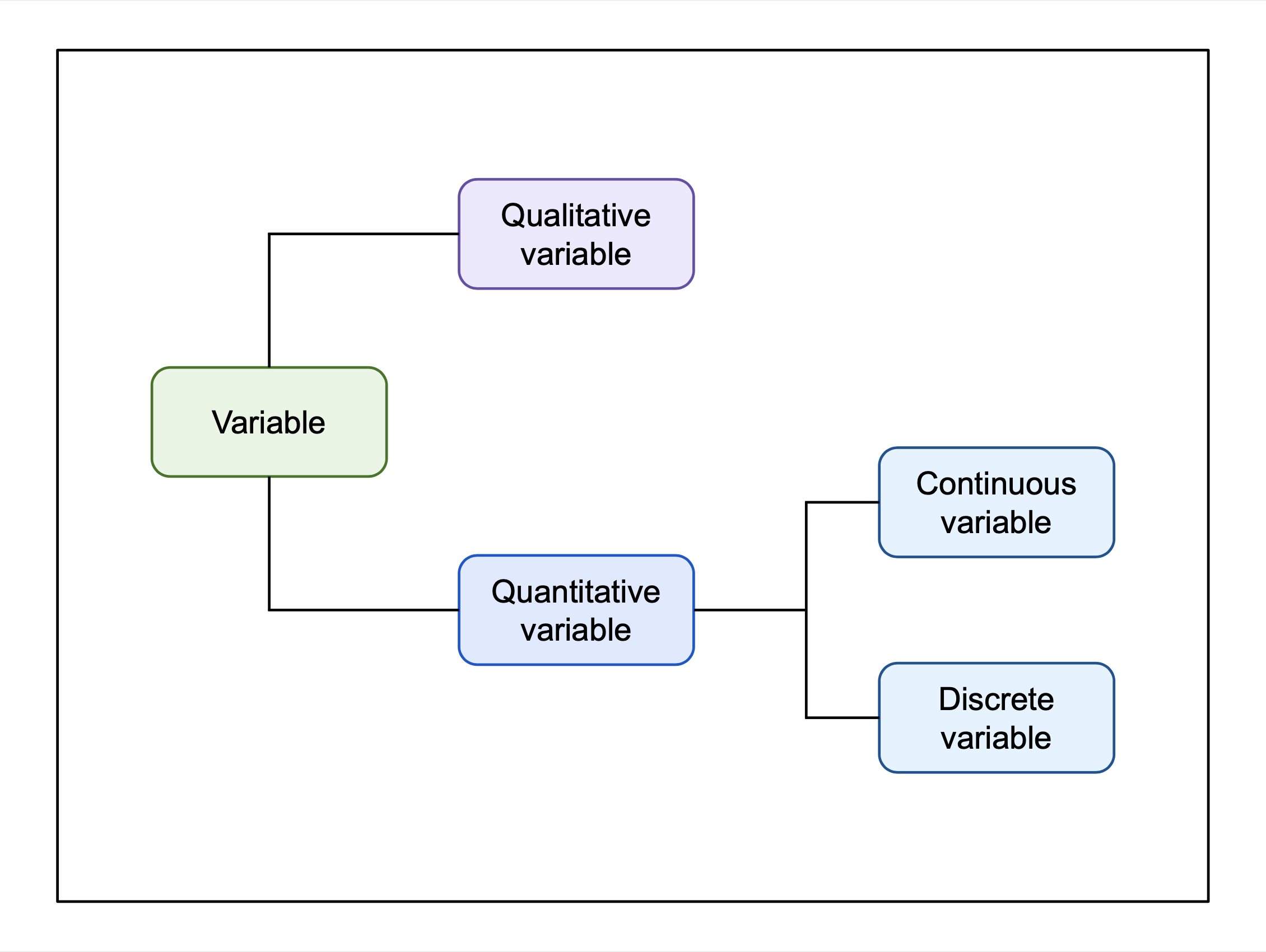
Quantitative Variable

In mathematics and statistics, a quantitative variable may be continuous or discrete. If it can take on two real values and all the values between them, the variable is continuous in that interval. If it can take on a value such that there is a non-infinitesimal gap on each side of it containing no values that the variable can take on, then it is discrete around that value. In some contexts, a variable can be discrete in some ranges of the number line and continuous in others. In statistics, continuous and discrete variables are distinct statistical data types which are described with different probability distributions.

Continuous variable

A continuous variable is a variable such that there are possible values between any two values.

For example, a variable over a non-empty range of the real numbers is continuous if it can take on any value in that range.

Methods of calculus are often used in problems in which the variables are continuous, for example in continuous optimization problems.

In statistical theory, the probability distributions of continuous variables can be expressed in terms of probability density functions.

In continuous-time dynamics, the variable ''time'' is treated as continuous, and the equation describing the evolution of some variable over time is a differential equation. The instantaneous rate of change is a well-defined concept that takes the ratio of the change in the dependent variable to the independent variable at a specific instant.

Discrete variable

In contrast, a variable is a discrete variable if and only if there exists a one-to-one correspondence between this variable and a subset of $\mathbb$, the set of natural numbers. In other words, a discrete variable over a particular interval of real values is one for which, for any value in the range that the variable is permitted to take on, there is a positive minimum distance to the nearest other permissible value. The number of permitted values is either finite or countably infinite. Common examples are variables that must be integers, non-negative integers, positive integers, or only the integers 0 and 1.

Methods of calculus do not readily lend themselves to problems involving discrete variables. Especially in multivariable calculus, many models rely on the assumption of continuity. Examples of problems involving discrete variables include integer programming.

In statistics, the probability distributions of discrete variables can be expressed in terms of probability mass functions.

In discrete time dynamics, the variable ''time'' is treated as discrete, and the equation of evolution of some variable over time is called a difference equation. For certain discrete-time dynamical systems, the system response can be modelled by solving the difference equation for an analytical solution.

In econometrics and more generally in regression analysis, sometimes some of the variables being empirically related to each other are 0-1 variables, being permitted to take on only those two values. The purpose of the discrete values of 0 and 1 is to use the dummy variable as a ‘switch’ that can ‘turn on’ and ‘turn off’ by assigning the two values to different parameters in an equation. A variable of this type is called a dummy variable. If the dependent variable is a dummy variable, then logistic regression or probit regression is commonly employed. In the case of regression analysis, a dummy variable can be used to represent subgroups of the sample in a study (e.g. the value 0 corresponding to a constituent of the control group).

Mixture of continuous and discrete variables

A mixed multivariate model can contain both discrete and continuous variables. For instance, a simple mixed multivariate model could have a discrete variable $x$, which only takes on values 0 or 1, and a continuous variable $y$. An example of a mixed model could be a research study on the risk of psychological disorders based on one binary measure of psychiatric symptoms and one continuous measure of cognitive performance. Mixed models may also involve a single variable that is discrete over some range of the number line and continuous at another range.

In probability theory and statistics, the probability distribution of a mixed random variable consists of both discrete and continuous components. A mixed random variable does not have a cumulative distribution function that is discrete or everywhere-continuous. An example of a mixed type random variable is the probability of wait time in a queue. The likelihood of a customer experiencing a zero wait time is discrete, while non-zero wait times are evaluated on a continuous time scale. In physics (particularly quantum mechanics, where this sort of distribution often arises), Dirac delta functions are often used to treat continuous and discrete components in a unified manner. For example, the previous example might be described by a probability density $p(t)=\alpha \delta (t) + g(t)$, such that $P(t>0)=\int_0^\infty g(t)=1-\alpha$, and $P(t=0)=\alpha$.

See also

* Continuous-time stochastic process
* Continuous function
* Continuous geometry
* Continuous modelling
* Continuous or discrete spectrum
* Continuous spectrum
* Count data
* Discrete-time stochastic process
* Discrete geometry
* Discrete mathematics
* Discrete measure
* Discrete modelling
* Discrete series representation
* Discrete space
* Discrete spectrum
* Discrete time and continuous time
* Discretization
* Interpolation
* Principal series representation (continuous series representation)

References

{{Reflist

Mathematical terminology
Statistical data types