Polyconic Projection Class on:
[Wikipedia]
[Google]
[Amazon]
Polyconic can refer either to a class of
"The Dietrich-Kitada Projection"
Table of examples and properties of all common projections
from radicalcartography.net Map projections {{cartography-stub
Polyconic can refer either to a class of map projection
In cartography, a map projection is any of a broad set of Transformation (function) , transformations employed to represent the curved two-dimensional Surface (mathematics), surface of a globe on a Plane (mathematics), plane. In a map projection, ...
s or to a specific projection known less ambiguously as the American polyconic projection
In the cartography of the United States, the American polyconic projection is a map projection used for maps of the United States and regions of the United States, its regions beginning early in the 19th century. It belongs to the polyconic proj ...
. Polyconic as a class refers to those projections whose parallels are all non-concentric circular arcs, except for a straight equator, and the centers of these circles lie along a central axis. This description applies to projections in equatorial aspect.
Polyconic projections
Some of the projections that fall into the polyconic class are: *American polyconic projection
In the cartography of the United States, the American polyconic projection is a map projection used for maps of the United States and regions of the United States, its regions beginning early in the 19th century. It belongs to the polyconic proj ...
—each parallel becomes a circular arc having true scale, the same scale as the central meridian
*Latitudinally equal-differential polyconic projection
The latitudinally equal-differential polyconic projection ( 等差分纬线多圆锥投影) is a polyconic map projection in use since 1963 in mainland China. Maps on this projection are produced by China's State Bureau of Surveying and Mapping an ...
*Rectangular polyconic projection
The rectangular polyconic projection is a map projection was first mentioned in 1853 by the United States Coast Survey, where it was developed and used for portions of the U.S. exceeding about one square degree. It belongs to the polyconic project ...
*Van der Grinten projection
The van der Grinten projection is a compromise map projection, which means that it is neither equal-area nor conformal. Unlike perspective projections, the van der Grinten projection is an arbitrary geometric construction on the plane. Van der ...
—projects entire earth into one circle; all meridians and parallels are arcs of circles.
* Nicolosi globular projection
The Nicolosi globular projection is a polyconic map projection invented about the year 1000 by the Iranian polymath al-Biruni. As a circular representation of a hemisphere, it is called ''globular'' because it evokes a globe. It can only display ...
—typically used to project a hemisphere into a circle; all meridians and parallels are arcs of circles.
A series of polyconic projections, each in a circle, was also presented by Hans Mauer in 1922, who also presented an equal-area polyconic in 1935.
Another series by Georgiy Aleksandrovich Ginzburg appeared starting in 1949.
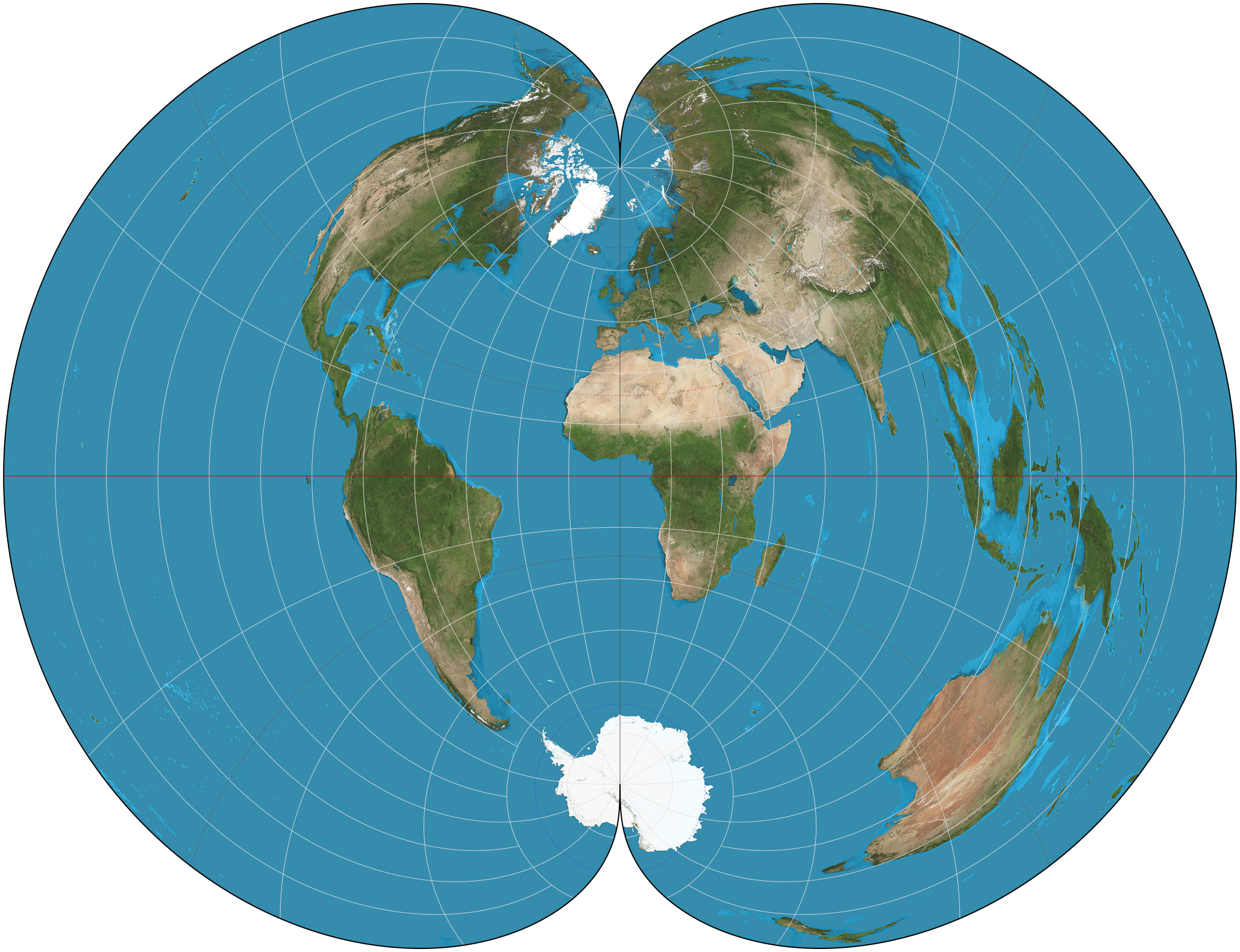
Most polyconic projections, when used to map the entire sphere, produce an "apple-shaped" map of the world.
There are many "apple-shaped" projections, almost all of them obscure.
John J. G. Savard"The Dietrich-Kitada Projection"
See also
*List of map projections
This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise WP:NOTABLE, notable. Because there is no limit to the number of possible map projections,
there can be no comprehensive list.
Table of proj ...
References
External links
Table of examples and properties of all common projections
from radicalcartography.net Map projections {{cartography-stub