|
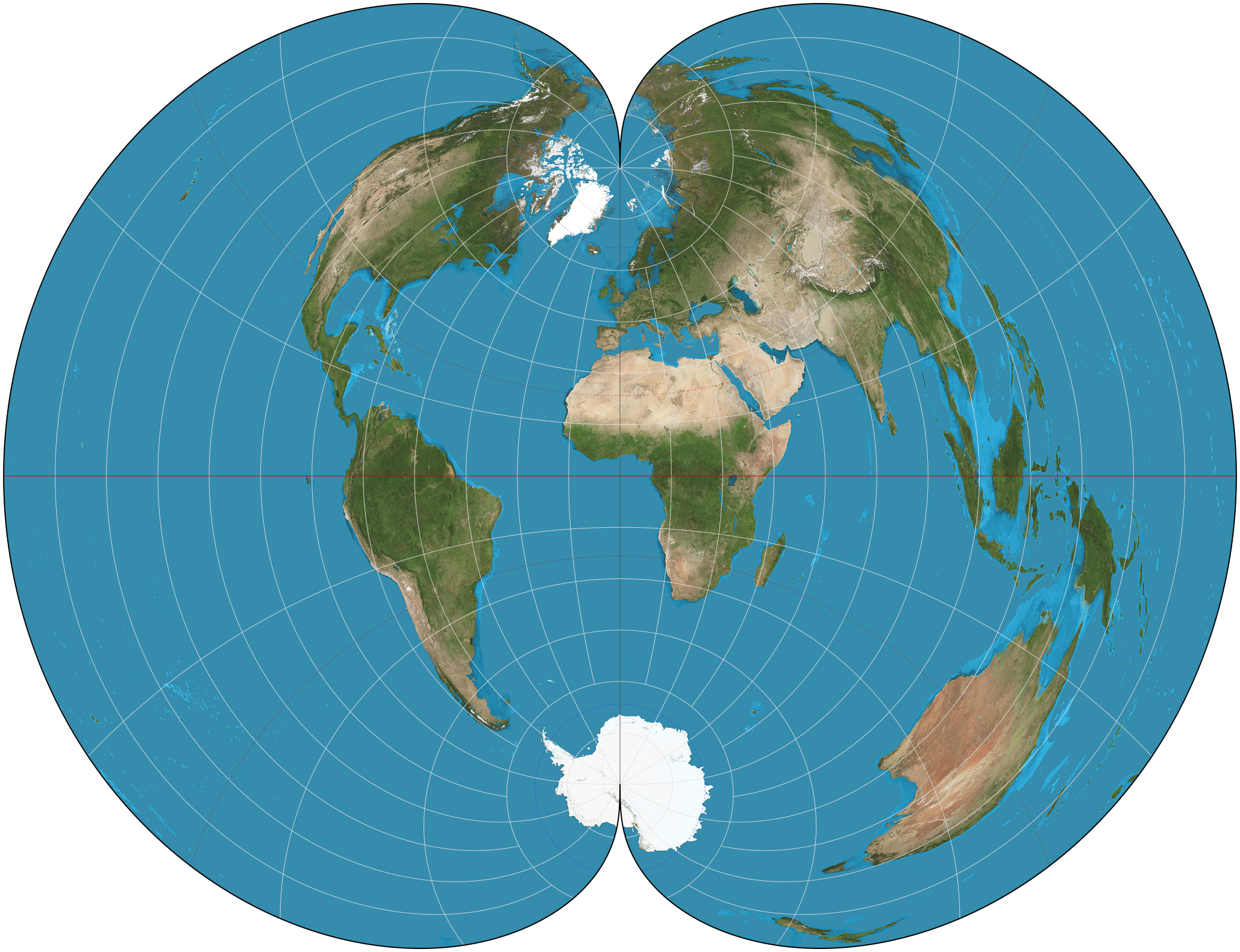
Latitudinally Equal-differential Polyconic Projection
The latitudinally equal-differential polyconic projection ( 等差分纬线多圆锥投影) is a polyconic map projection in use since 1963 in mainland China. Maps on this projection are produced by China's State Bureau of Surveying and Mapping and other publishers. Its original method of construction has not been preserved, but a mathematical approximation has been published. Description As a polyconic projection, the parallels are arcs of circles that are not concentric. The points of no distortion are on the central meridian at 44°N/S latitude. Meridians are convex away from the straight central meridian, and parallels are gently concave away from the equator. The projection is neither equal-area nor conformal; rather, it is a compromise projection. Maps on this projection do not show the north pole, instead cropping the high latitudes along a straight line whose latitude varies but that never reaches the pole. By convention, the projection is centered at 150° such that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyconic Projection Class
Polyconic can refer either to a class of map projections or to a specific projection known less ambiguously as the American polyconic projection. Polyconic as a class refers to those projections whose parallels are all non-concentric circular arcs, except for a straight equator, and the centers of these circles lie along a central axis. This description applies to projections in equatorial aspect. Polyconic projections Some of the projections that fall into the polyconic class are: *American polyconic projection—each parallel becomes a circular arc having true scale, the same scale as the central meridian * Latitudinally equal-differential polyconic projection * Rectangular polyconic projection * Van der Grinten projection—projects entire earth into one circle; all meridians and parallels are arcs of circles. * Nicolosi globular projection—typically used to project a hemisphere into a circle; all meridians and parallels are arcs of circles. A series of polyconic projection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Map Projection
In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way and to some extent. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, projections are considered in several ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
China
China, officially the People's Republic of China (PRC), is a country in East Asia. It is the world's List of countries and dependencies by population, most populous country, with a Population of China, population exceeding 1.4 billion, slightly ahead of India. China spans the equivalent of five time zones and Borders of China, borders fourteen countries by land, the List of countries and territories by land borders, most of any country in the world, tied with Russia. Covering an area of approximately , it is the world's third List of countries and dependencies by area, largest country by total land area. The country consists of 22 provinces of China, provinces, five autonomous regions of China, autonomous regions, four direct-administered municipalities of China, municipalities, and two special administrative regions of China, Special Administrative Regions (Hong Kong and Macau). The national capital is Beijing, and the List of cities in China by population, most populous cit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arc (geometry)
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that appeared more than 2000 years ago in Euclid's ''Elements'': "The urvedline is ��the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which ��will leave from its imaginary moving some vestige in length, exempt of any width." This definition of a curve has been formalized in modern mathematics as: ''A curve is the image of an interval to a topological space by a continuous function''. In some contexts, the function that defines the curve is called a ''parametrization'', and the curve is a parametric curve. In this article, these curves are sometimes called ''topological curves'' to distinguish them from more constrained curves suc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Map Projections
This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise notable Notability is the property of being worthy of notice, having fame, or being considered to be of a high degree of interest, significance, or distinction. It also refers to the capacity to be such. Persons who are notable due to public responsibi .... Because there is no limit to the number of possible map projections, there can be no comprehensive list. Table of projections *The first known popularizer/user and not necessarily the creator. Key Type of projection ; Cylindrical: In standard presentation, these map regularly-spaced meridians to equally spaced vertical lines, and parallels to horizontal lines. ; Pseudocylindrical: In standard presentation, these map the central meridian and parallels as straight lines. Other meridians are curves (or possibly straight from pole to equator), regularly spaced along parallels. ; Conic: In standard presentation, conic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Winkel Tripel Projection
The Winkel tripel projection (Winkel III), a modified azimuthal map projection of the world, is one of three projections proposed by German cartographer Oswald Winkel (7 January 1874 – 18 July 1953) in 1921. The projection is the arithmetic mean of the equirectangular projection and the Aitoff projection: The name ( German for 'triple') refers to Winkel's goal of minimizing three kinds of distortion: area, direction, and distance. Algorithm : \begin x &= \frac \left(\lambda \cos \varphi_1 + \frac\right), \\ y &= \frac \left(\varphi + \frac\right), \end where ''λ'' is the longitude relative to the central meridian of the projection, ''φ'' is the latitude, ''φ'' is the standard parallel for the equirectangular projection, sinc is the unnormalized cardinal sine function, and : \alpha = \arccos\left(\cos\varphi \cos \frac \right). In his proposal, Winkel set : \varphi_1 = \arccos \frac. A closed-form inverse mapping does not exist, and computing the inverse numeri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |