Polar Coordinates System on:
[Wikipedia]
[Google]
[Amazon]
In
 The equation defining a
The equation defining a
 The
The
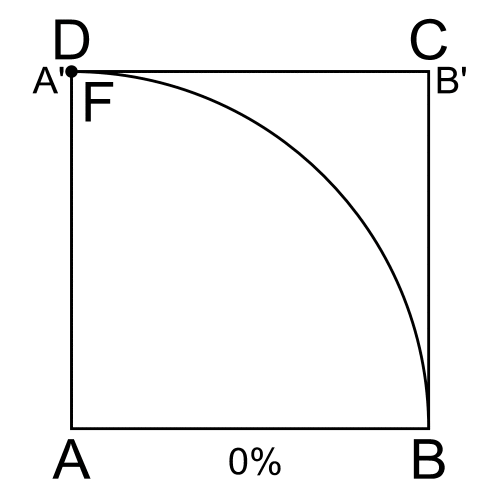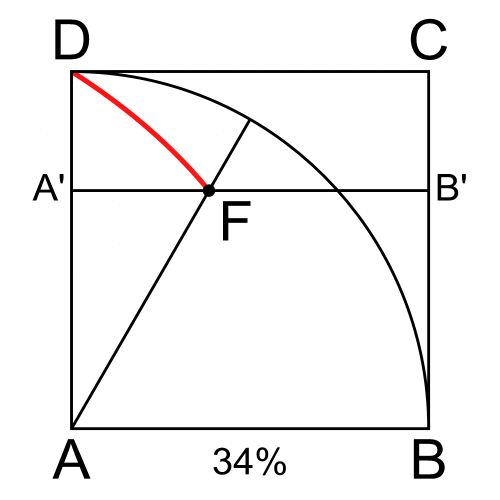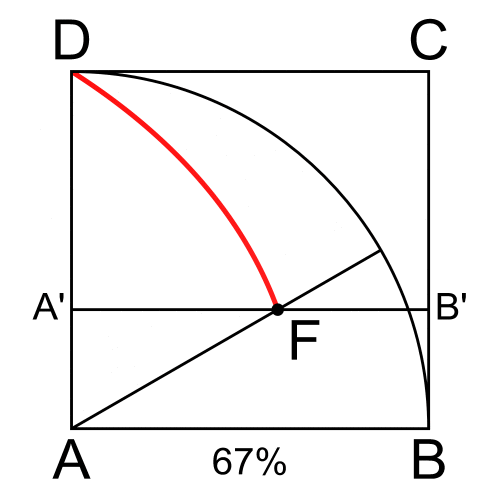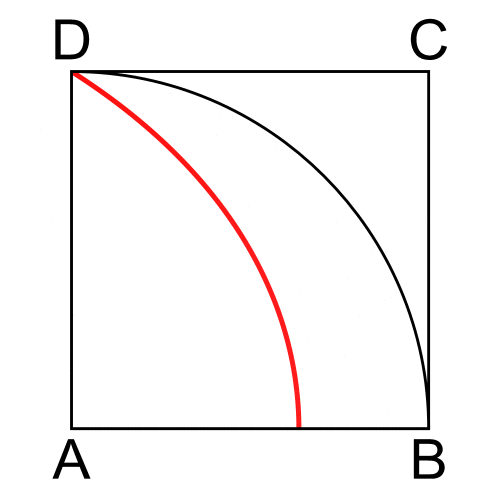 A quadratrix in the first quadrant (''x, y'') is a curve with ''y'' = ρ sin θ equal to the fraction of the quarter circle with radius ''r'' determined by the radius through the curve point. Since this fraction is , the curve is given by .
A quadratrix in the first quadrant (''x, y'') is a curve with ''y'' = ρ sin θ equal to the fraction of the quarter circle with radius ''r'' determined by the radius through the curve point. Since this fraction is , the curve is given by .
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, the polar coordinate system specifies a given point in a plane
Plane most often refers to:
* Aero- or airplane, a powered, fixed-wing aircraft
* Plane (geometry), a flat, 2-dimensional surface
* Plane (mathematics), generalizations of a geometrical plane
Plane or planes may also refer to:
Biology
* Plane ...
by using a distance and an angle as its two coordinates
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine and standardize the Position (geometry), position of the Point (geometry), points or other geometric elements on a manifold such as ...
. These are
*the point's distance from a reference point called the ''pole'', and
*the point's direction from the pole relative to the direction of the ''polar axis'', a ray drawn from the pole.
The distance from the pole is called the ''radial coordinate'', ''radial distance'' or simply ''radius'', and the angle is called the ''angular coordinate'', ''polar angle'', or ''azimuth
An azimuth (; from ) is the horizontal angle from a cardinal direction, most commonly north, in a local or observer-centric spherical coordinate system.
Mathematically, the relative position vector from an observer ( origin) to a point ...
''. The pole is analogous to the origin in a Cartesian coordinate system
In geometry, a Cartesian coordinate system (, ) in a plane (geometry), plane is a coordinate system that specifies each point (geometry), point uniquely by a pair of real numbers called ''coordinates'', which are the positive and negative number ...
.
Polar coordinates are most appropriate in any context where the phenomenon being considered is inherently tied to direction and length from a center point in a plane, such as spiral
In mathematics, a spiral is a curve which emanates from a point, moving further away as it revolves around the point. It is a subtype of whorled patterns, a broad group that also includes concentric objects.
Two-dimensional
A two-dimension ...
s. Planar physical systems with bodies moving around a central point, or phenomena originating from a central point, are often simpler and more intuitive to model using polar coordinates.
The polar coordinate system is extended to three dimensions in two ways: the cylindrical coordinate system
A cylindrical coordinate system is a three-dimensional coordinate system that specifies point positions around a main axis (a chosen directed line) and an auxiliary axis (a reference ray). The three cylindrical coordinates are: the point perpen ...
adds a second distance coordinate, and the spherical coordinate system
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are
* the radial distance along the line connecting the point to a fixed point ...
adds a second angular coordinate.
Grégoire de Saint-Vincent
Grégoire de Saint-Vincent () - in Latin : Gregorius a Sancto Vincentio, in Dutch : Gregorius van St-Vincent - (8 September 1584 Bruges – 5 June 1667 Ghent) was a Flemish Jesuit and mathematician. He is remembered for his work on quadrature of ...
and Bonaventura Cavalieri
Bonaventura Francesco Cavalieri (; 1598 – 30 November 1647) was an Italian mathematician and a Jesuati, Jesuate. He is known for his work on the problems of optics and motion (physics), motion, work on indivisibles, the precursors of infin ...
independently introduced the system's concepts in the mid-17th century, though the actual term ''polar coordinates'' has been attributed to Gregorio Fontana in the 18th century. The initial motivation for introducing the polar system was the study of circular
Circular may refer to:
* The shape of a circle
* ''Circular'' (album), a 2006 album by Spanish singer Vega
* Circular letter (disambiguation), a document addressed to many destinations
** Government circular, a written statement of government pol ...
and orbital motion
In celestial mechanics, an orbit (also known as orbital revolution) is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an obj ...
.
History
The concepts of angle and radius were already used by ancient peoples of the first millennium BC. The Greek astronomer andastrologer
Astrology is a range of Divination, divinatory practices, recognized as pseudoscientific since the 18th century, that propose that information about human affairs and terrestrial events may be discerned by studying the apparent positions ...
Hipparchus
Hipparchus (; , ; BC) was a Ancient Greek astronomy, Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry, but is most famous for his incidental discovery of the precession of the equinoxes. Hippar ...
(190–120 BC) created a table of chord functions giving the length of the chord for each angle, and there are references to his using polar coordinates in establishing stellar positions. In ''On Spirals
''On Spirals'' () is a treatise by Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, S ...
'', Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
describes the Archimedean spiral
The Archimedean spiral (also known as Archimedes' spiral, the arithmetic spiral) is a spiral named after the 3rd-century BC Ancient Greece, Greek mathematician Archimedes. The term ''Archimedean spiral'' is sometimes used to refer to the more gene ...
, a function whose radius depends on the angle. The Greek work, however, did not extend to a full coordinate system.
From the 8th century AD onward, astronomers developed methods for approximating and calculating the direction to Mecca
Mecca, officially Makkah al-Mukarramah, is the capital of Mecca Province in the Hejaz region of western Saudi Arabia; it is the Holiest sites in Islam, holiest city in Islam. It is inland from Jeddah on the Red Sea, in a narrow valley above ...
(qibla
The qibla () is the direction towards the Kaaba in the Great Mosque of Mecca, Sacred Mosque in Mecca, which is used by Muslims in various religious contexts, particularly the direction of prayer for the salah. In Islam, the Kaaba is believed to ...
)—and its distance—from any location on the Earth. From the 9th century onward they were using spherical trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the edge (geometry), sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, ge ...
and map projection
In cartography, a map projection is any of a broad set of Transformation (function) , transformations employed to represent the curved two-dimensional Surface (mathematics), surface of a globe on a Plane (mathematics), plane. In a map projection, ...
methods to determine these quantities accurately. The calculation is essentially the conversion of the equatorial polar coordinates of Mecca (i.e. its longitude
Longitude (, ) is a geographic coordinate that specifies the east- west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek lett ...
and latitude
In geography, latitude is a geographic coordinate system, geographic coordinate that specifies the north-south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from −90° at t ...
) to its polar coordinates (i.e. its qibla and distance) relative to a system whose reference meridian is the great circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point.
Discussion
Any arc of a great circle is a geodesic of the sphere, so that great circles in spher ...
through the given location and the Earth's poles and whose polar axis is the line through the location and its antipodal point
In mathematics, two points of a sphere (or n-sphere, including a circle) are called antipodal or diametrically opposite if they are the endpoints of a diameter, a straight line segment between two points on a sphere and passing through its cen ...
.
There are various accounts of the introduction of polar coordinates as part of a formal coordinate system. The full history of the subject is described in Harvard
Harvard University is a private Ivy League research university in Cambridge, Massachusetts, United States. Founded in 1636 and named for its first benefactor, the Puritan clergyman John Harvard, it is the oldest institution of higher lear ...
professor Julian Lowell Coolidge's ''Origin of Polar Coordinates.'' Grégoire de Saint-Vincent and Bonaventura Cavalieri independently introduced the concepts in the mid-seventeenth century. Saint-Vincent wrote about them privately in 1625 and published his work in 1647, while Cavalieri published his in 1635 with a corrected version appearing in 1653. Cavalieri first used polar coordinates to solve a problem relating to the area within an Archimedean spiral
The Archimedean spiral (also known as Archimedes' spiral, the arithmetic spiral) is a spiral named after the 3rd-century BC Ancient Greece, Greek mathematician Archimedes. The term ''Archimedean spiral'' is sometimes used to refer to the more gene ...
. Blaise Pascal
Blaise Pascal (19June 162319August 1662) was a French mathematician, physicist, inventor, philosopher, and Catholic Church, Catholic writer.
Pascal was a child prodigy who was educated by his father, a tax collector in Rouen. His earliest ...
subsequently used polar coordinates to calculate the length of parabolic arcs.
In ''Method of Fluxions
''Method of Fluxions'' () is a mathematical treatise by Sir Isaac Newton which served as the earliest written formulation of modern calculus. The book was completed in 1671 and posthumously published in 1736. Background
Fluxion is Newton's term ...
'' (written 1671, published 1736), Sir Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed ...
examined the transformations between polar coordinates, which he referred to as the "Seventh Manner; For Spirals", and nine other coordinate systems. In the journal ''Acta Eruditorum
(from Latin: ''Acts of the Erudite'') was the first scientific journal of the German-speaking lands of Europe, published from 1682 to 1782.
History
''Acta Eruditorum'' was founded in 1682 in Leipzig by Otto Mencke, who became its first edit ...
'' (1691), Jacob Bernoulli
Jacob Bernoulli (also known as James in English or Jacques in French; – 16 August 1705) was a Swiss mathematician. He sided with Gottfried Wilhelm Leibniz during the Leibniz–Newton calculus controversy and was an early proponent of Leibniz ...
used a system with a point on a line, called the ''pole'' and ''polar axis'' respectively. Coordinates were specified by the distance from the pole and the angle from the ''polar axis''. Bernoulli's work extended to finding the radius of curvature
In differential geometry, the radius of curvature, , is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius ...
of curves expressed in these coordinates.
The actual term ''polar coordinates'' has been attributed to Gregorio Fontana and was used by 18th-century Italian writers. The term appeared in English in George Peacock
George Peacock FRS (9 April 1791 – 8 November 1858) was an English mathematician and Anglican cleric. He founded what has been called the British algebra of logic.
Early life
Peacock was born on 9 April 1791 at Thornton Hall, Denton, nea ...
's 1816 translation of Lacroix's ''Differential and Integral Calculus''. Alexis Clairaut
Alexis Claude Clairaut (; ; 13 May 1713 – 17 May 1765) was a French mathematician, astronomer, and geophysicist. He was a prominent Newtonian whose work helped to establish the validity of the principles and results that Isaac Newton, Sir Isaa ...
was the first to think of polar coordinates in three dimensions, and Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...
was the first to actually develop them.
Conventions
The radial coordinate is often denoted by ''r'' or ''ρ'', and the angular coordinate by ''φ'', ''θ'', or ''t''. The angular coordinate is specified as ''φ'' byISO
The International Organization for Standardization (ISO ; ; ) is an independent, non-governmental, international standard development organization composed of representatives from the national standards organizations of member countries.
Me ...
standard 31-11, now 80000-2:2019. However, in mathematical literature the angle is often denoted by θ instead.
Angles in polar notation are generally expressed in either degrees or radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...
s (2 rad being equal to 360°). Degrees are traditionally used in navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the motion, movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navig ...
, surveying
Surveying or land surveying is the technique, profession, art, and science of determining the land, terrestrial Plane (mathematics), two-dimensional or Three-dimensional space#In Euclidean geometry, three-dimensional positions of Point (geom ...
, and many applied disciplines, while radians are more common in mathematics and mathematical physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
.
The angle ''φ'' is defined to start at 0° from a ''reference direction'', and to increase for rotations in either clockwise (cw) or counterclockwise (ccw) orientation. For example, in mathematics, the reference direction is usually drawn as a ray from the pole horizontally to the right, and the polar angle increases to positive angles for ccw rotations, whereas in navigation ( bearing, heading) the 0°-heading is drawn vertically upwards and the angle increases for cw rotations. The polar angles decrease towards negative values for rotations in the respectively opposite orientations.
Uniqueness of polar coordinates
Adding any number of full turns (360°) to the angular coordinate does not change the corresponding direction. Similarly, any polar coordinate is identical to the coordinate with the negative radial component and the opposite direction (adding 180° to the polar angle). Therefore, the same point (''r'', ''φ'') can be expressed with an infinite number of different polar coordinates and , where ''n'' is an arbitraryinteger
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
. Moreover, the pole itself can be expressed as (0, ''φ'') for any angle ''φ''.
Where a unique representation is needed for any point besides the pole, it is usual to limit ''r'' to positive numbers () and ''φ'' to either the interval or the interval , which in radians are or . Another convention, in reference to the usual codomain
In mathematics, a codomain, counter-domain, or set of destination of a function is a set into which all of the output of the function is constrained to fall. It is the set in the notation . The term '' range'' is sometimes ambiguously used to ...
of the arctan function, is to allow for arbitrary nonzero real values of the radial component and restrict the polar angle to . In all cases a unique azimuth for the pole (''r'' = 0) must be chosen, e.g., ''φ'' = 0.
Converting between polar and Cartesian coordinates
The polar coordinates ''r'' and ''φ'' can be converted to the Cartesian coordinates ''x'' and ''y'' by using thetrigonometric function
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all ...
s sine and cosine:
The Cartesian coordinates ''x'' and ''y'' can be converted to polar coordinates ''r'' and ''φ'' with ''r'' ≥ 0 and ''φ'' in the interval (−, ] by:
where hypot is the Pythagorean addition, Pythagorean sum and atan2
In computing and mathematics, the function (mathematics), function atan2 is the 2-Argument of a function, argument arctangent. By definition, \theta = \operatorname(y, x) is the angle measure (in radians, with -\pi 0, \\ mu \arctan\left(\fr ...
is a common variation on the arctangent
In mathematics, the inverse trigonometric functions (occasionally also called ''antitrigonometric'', ''cyclometric'', or ''arcus'' functions) are the inverse functions of the trigonometric functions, under suitably restricted domains. Specific ...
function defined as
If ''r'' is calculated first as above, then this formula for ''φ'' may be stated more simply using the arccosine
In mathematics, the inverse trigonometric functions (occasionally also called ''antitrigonometric'', ''cyclometric'', or ''arcus'' functions) are the inverse functions of the trigonometric functions, under suitably restricted domains. Specific ...
function:
Complex numbers
Everycomplex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
can be represented as a point in the complex plane
In mathematics, the complex plane is the plane (geometry), plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal -axis, called the real axis, is formed by the real numbers, and the vertical -axis, call ...
, and can therefore be expressed by specifying either the point's Cartesian coordinates (called rectangular or Cartesian form) or the point's polar coordinates (called polar form).
In polar form, the distance and angle coordinates are often referred to as the number's magnitude and argument respectively. Two complex numbers can be multiplied by adding their arguments and multiplying their magnitudes.
The complex number ''z'' can be represented in rectangular form as
where ''i'' is the imaginary unit
The imaginary unit or unit imaginary number () is a mathematical constant that is a solution to the quadratic equation Although there is no real number with this property, can be used to extend the real numbers to what are called complex num ...
, or can alternatively be written in polar form as
and from there, by Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for ...
, as
where ''e'' is Euler's number
The number is a mathematical constant approximately equal to 2.71828 that is the base of the natural logarithm and exponential function. It is sometimes called Euler's number, after the Swiss mathematician Leonhard Euler, though this can ...
, and ''φ'', expressed in radians, is the principal value
In mathematics, specifically complex analysis, the principal values of a multivalued function are the values along one chosen branch (mathematical analysis), branch of that Function (mathematics), function, so that it is Single-valued function, ...
of the complex number function arg applied to ''x'' + ''iy''. To convert between the rectangular and polar forms of a complex number, the conversion formulae given above can be used. Equivalent are the and angle notation
In physics and engineering, a phasor (a portmanteau of phase vector) is a complex number representing a sinusoidal function whose amplitude and initial phase are time-invariant and whose angular frequency is fixed. It is related to a mor ...
s:
For the operations of multiplication
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division (mathematics), division. The result of a multiplication operation is called a ''Product (mathem ...
, division, exponentiation
In mathematics, exponentiation, denoted , is an operation (mathematics), operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication ...
, and root extraction of complex numbers, it is generally much simpler to work with complex numbers expressed in polar form rather than rectangular form. From the laws of exponentiation:
; Multiplication:
; Division:
; Exponentiation ( De Moivre's formula):
; Root Extraction (Principal root):
Polar equation of a curve
 The equation defining a
The equation defining a plane curve
In mathematics, a plane curve is a curve in a plane that may be a Euclidean plane, an affine plane or a projective plane. The most frequently studied cases are smooth plane curves (including piecewise smooth plane curves), and algebraic plane c ...
expressed in polar coordinates is known as a ''polar equation''. In many cases, such an equation can simply be specified by defining ''r'' as a function
Function or functionality may refer to:
Computing
* Function key, a type of key on computer keyboards
* Function model, a structured representation of processes in a system
* Function object or functor or functionoid, a concept of object-orie ...
of ''φ''. The resulting curve then consists of points of the form (''r''(''φ''), ''φ'') and can be regarded as the graph
Graph may refer to:
Mathematics
*Graph (discrete mathematics), a structure made of vertices and edges
**Graph theory, the study of such graphs and their properties
*Graph (topology), a topological space resembling a graph in the sense of discret ...
of the polar function ''r''. Note that, in contrast to Cartesian coordinates, the independent variable ''φ'' is the ''second'' entry in the ordered pair.
Different forms of symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
can be deduced from the equation of a polar function ''r'':
* If the curve will be symmetrical about the horizontal (0°/180°) ray;
* If it will be symmetric about the vertical (90°/270°) ray:
* If it will be rotationally symmetric
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which ...
by α clockwise and counterclockwise about the pole.
Because of the circular nature of the polar coordinate system, many curves can be described by a rather simple polar equation, whereas their Cartesian form is much more intricate. Among the best known of these curves are the polar rose, Archimedean spiral
The Archimedean spiral (also known as Archimedes' spiral, the arithmetic spiral) is a spiral named after the 3rd-century BC Ancient Greece, Greek mathematician Archimedes. The term ''Archimedean spiral'' is sometimes used to refer to the more gene ...
, lemniscate
In algebraic geometry, a lemniscate ( or ) is any of several figure-eight or -shaped curves. The word comes from the Latin , meaning "decorated with ribbons", from the Greek (), meaning "ribbon",. or which alternatively may refer to the wool fr ...
, limaçon
In geometry, a limaçon or limacon , also known as a limaçon of Pascal or Pascal's Snail, is defined as a roulette curve formed by the path of a point fixed to a circle when that circle rolls around the outside of a circle of equal radius. I ...
, and cardioid
In geometry, a cardioid () is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal ...
.
For the circle, line, and polar rose below, it is understood that there are no restrictions on the domain and range of the curve.
Circle
The general equation for a circle with a center at and radius ''a'' is This can be simplified in various ways, to conform to more specific cases, such as the equation for a circle with a center at the pole and radius ''a''. When or the origin lies on the circle, the equation becomes In the general case, the equation can be solved for , giving The solution with a minus sign in front of the square root gives the same curve.Line
''Radial'' lines (those running through the pole) are represented by the equation where is the angle of elevation of the line; that is, , where is theslope
In mathematics, the slope or gradient of a Line (mathematics), line is a number that describes the direction (geometry), direction of the line on a plane (geometry), plane. Often denoted by the letter ''m'', slope is calculated as the ratio of t ...
of the line in the Cartesian coordinate system. The non-radial line that crosses the radial line perpendicular
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', � ...
ly at the point has the equation
Otherwise stated is the point in which the tangent intersects the imaginary circle of radius
Polar rose
A polar rose is a mathematical curve that looks like a petaled flower, and that can be expressed as a simple polar equation, for any constant γ0 (including 0). If ''k'' is an integer, these equations will produce a ''k''-petaled rose if ''k'' is odd, or a 2''k''-petaled rose if ''k'' is even. If ''k'' is rational, but not an integer, a rose-like shape may form but with overlapping petals. Note that these equations never define a rose with 2, 6, 10, 14, etc. petals. The variable ''a'' directly represents the length or amplitude of the petals of the rose, while ''k'' relates to their spatial frequency. The constant γ0 can be regarded as a phase angle.Archimedean spiral
Archimedean spiral
The Archimedean spiral (also known as Archimedes' spiral, the arithmetic spiral) is a spiral named after the 3rd-century BC Ancient Greece, Greek mathematician Archimedes. The term ''Archimedean spiral'' is sometimes used to refer to the more gene ...
is a spiral discovered by Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
which can also be expressed as a simple polar equation. It is represented by the equation
Changing the parameter ''a'' will turn the spiral, while ''b'' controls the distance between the arms, which for a given spiral is always constant. The Archimedean spiral has two arms, one for and one for . The two arms are smoothly connected at the pole. If , taking the mirror image of one arm across the 90°/270° line will yield the other arm. This curve is notable as one of the first curves, after the conic section
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, tho ...
s, to be described in a mathematical treatise, and as a prime example of a curve best defined by a polar equation.
Conic sections
Aconic section
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, tho ...
with one focus on the pole and the other somewhere on the 0° ray (so that the conic's major axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longe ...
lies along the polar axis) is given by:
where ''e'' is the eccentricity
Eccentricity or eccentric may refer to:
* Eccentricity (behavior), odd behavior on the part of a person, as opposed to being "normal"
Mathematics, science and technology Mathematics
* Off-Centre (geometry), center, in geometry
* Eccentricity (g ...
and is the semi-latus rectum
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, thou ...
(the perpendicular distance at a focus from the major axis to the curve). If , this equation defines a hyperbola
In mathematics, a hyperbola is a type of smooth function, smooth plane curve, curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected component ( ...
; if , it defines a parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactl ...
; and if , it defines an ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
. The special case of the latter results in a circle of the radius .
Quadratrix
 A quadratrix in the first quadrant (''x, y'') is a curve with ''y'' = ρ sin θ equal to the fraction of the quarter circle with radius ''r'' determined by the radius through the curve point. Since this fraction is , the curve is given by .
A quadratrix in the first quadrant (''x, y'') is a curve with ''y'' = ρ sin θ equal to the fraction of the quarter circle with radius ''r'' determined by the radius through the curve point. Since this fraction is , the curve is given by .
Intersection of two polar curves
The graphs of two polar functions and have possible intersections of three types: # In the origin, if the equations and have at least one solution each. # All the points