Plane Of Polarization

For light and other electromagnetic radiation, the plane of polarization is the plane spanned by the direction of propagation and either the electric vector or the magnetic vector, depending on the convention. It can be defined for polarized light, remains fixed in space for '' linearly-polarized'' light, and undergoes axial rotation for '' circularly-polarized'' light.

Unfortunately the two conventions are contradictory. As originally defined by Étienne-Louis Malus in 1811,Buchwald, 1989, p.54. the plane of polarization coincided (although this was not known at the time) with the plane containing the direction of propagation and the ''magnetic'' vector. In modern literature, the term ''plane of polarization'', if it is used at all, is likely to mean the plane containing the direction of propagation and the ''electric'' vector, because the electric field has the greater propensity to interact with matter.Born & Wolf, 1970, p.28.

For waves in a birefringent (doubly-refractive) crystal, under the old definition, one must also specify whether the direction of propagation means the ray direction (Poynting vector) or the wave- normal direction, because these directions generally differ and are both perpendicular to the magnetic vector (Fig.1). Malus, as an adherent of the corpuscular theory of light, could only choose the ray direction. But Augustin-Jean Fresnel, in his successful effort to explain double refraction under the wave theory (1822 onward), found it more useful to choose the wave-normal direction, with the result that the supposed vibrations of the medium were then consistently perpendicular to the plane of polarization.Fresnel, 1827, tr. Hobson, p.318. In an isotropic medium such as air, the ray and wave-normal directions are the same, and Fresnel's modification makes no difference.

Fresnel also admitted that, had he not felt constrained by the received terminology, it would have been more natural to define the plane of polarization as the plane containing the vibrations and the direction of propagation.Fresnel, 1822, tr. Young, part 7
p.406
That plane, which became known as the plane of vibration, is perpendicular to Fresnel's "plane of polarization" but identical with the plane that modern writers tend to call by that name!

It has been argued that the term ''plane of polarization'', because of its historical ambiguity, should be avoided in original writing. One can easily specify the orientation of a particular field vector; and even the term ''plane of vibration'' carries less risk of confusion than ''plane of polarization''.

Physics of the term

For electromagnetic (EM) waves in an ''isotropic'' medium (that is, a medium whose properties are independent of direction), the electric field vectors (E and D) are in one direction, and the magnetic field vectors (B and H) are in another direction, perpendicular to the first, and the direction of propagation is perpendicular to both the electric and the magnetic vectors. In this case the direction of propagation is both the ''ray'' direction and the ''wave-normal'' direction (the direction perpendicular to the wavefront). 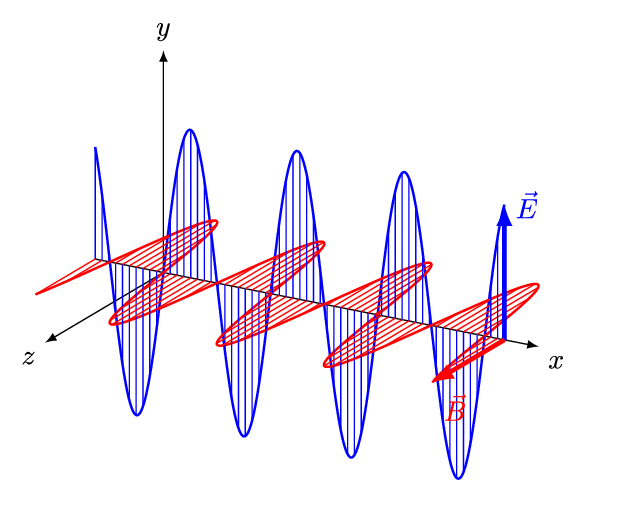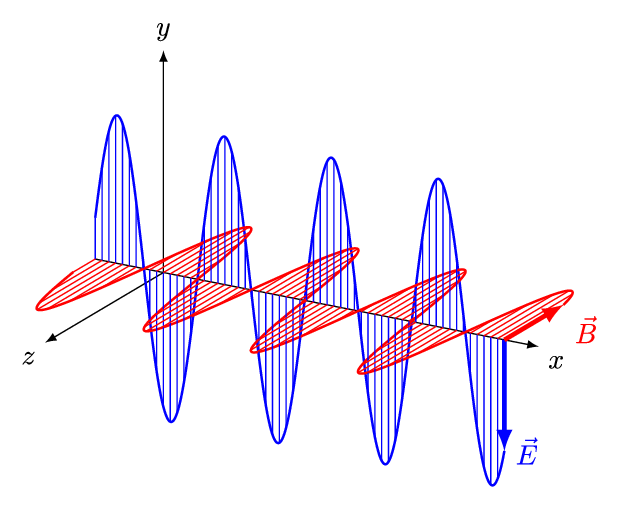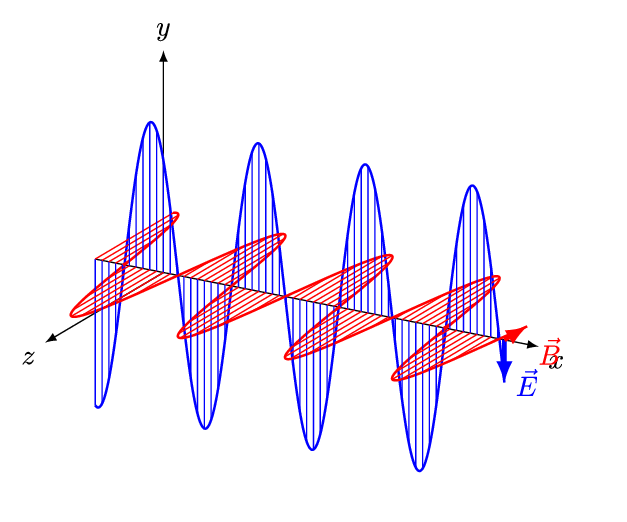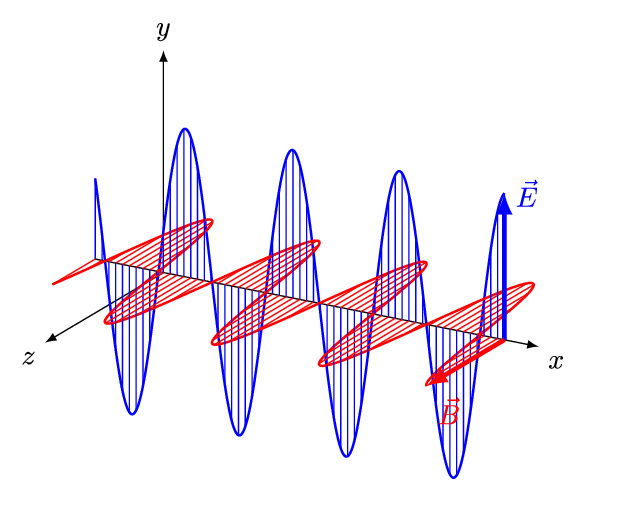For a ''linearly''-polarized wave (also called a ''plane''-polarized wave), the orientations of the field vectors are fixed (Fig.2).

Because innumerable materials are dielectrics or conductors while comparatively few are ferromagnets, the reflection or refraction of EM waves (including light) is more often due to differences in the ''electric'' properties of media than to differences in their magnetic properties. That circumstance tends to draw attention to the ''electric'' vectors, so that we tend to think of the direction of polarization as the direction of the electric vectors, and the "plane of polarization" as the plane containing the electric vectors and the direction of propagation.

Indeed, that is the convention used in the online ''Encyclopædia Britannica'', and in Feynman's lecture on polarization. In the latter case one must infer the convention from the context: Feynman keeps emphasizing the direction of the ''electric'' (E) vector and leaves the reader to presume that the "plane of polarization" contains that vector — and this interpretation indeed fits the examples he gives. The same vector is used to describe the polarization of radio signals and antennas (Fig.3).Stratton, 1941, p.280.

If the medium is magnetically isotropic but electrically ''non''-isotropic (like a doubly-refracting crystal), the magnetic vectors B and H are still parallel, and the electric vectors E and D are still perpendicular to both, and the ray direction is still perpendicular to E and the magnetic vectors, and the wave-normal direction is still perpendicular to D and the magnetic vectors; but there is generally a small angle between the electric vectors E and D, hence the same angle between the ray direction and the wave-normal direction (Fig.1). Hence D, E, the wave-normal direction, and the ray direction are all in the same plane, and it is all the more natural to define that plane as the "plane of polarization".

This "natural" definition, however, depends on the theory of EM waves developed by James Clerk Maxwell in the 1860s — whereas the word ''polarization'' was coined about 50 years earlier, and the associated mystery dates back even further.

History of the term

Three candidates

Whether by accident or by design, the plane of polarization has always been defined as the plane containing a field vector and a direction of propagation. In Fig.1, there are three such planes, to which we may assign numbers for ease of reference:
:(1)  the plane containing both electric vectors and both propagation directions  (i.e., the plane normal to the magnetic vectors);

:(2a)  the plane containing the magnetic vectors and the wave-normal  (i.e., the plane normal to D);

:(2b)  the plane containing the magnetic vectors and the ray  (i.e., the plane normal to E).
In an isotropic medium, E and D have the same direction,This conclusion does not follow if the medium is optically rotating (see e.g. Darrigol, 2012, pp.253n,257n); however, throughout this article, the existence of a stable plane of polarization requires the absence of optical rotation. so that the ray and wave-normal directions merge, and the planes (2a) and (2b) become one:
:(2)  the plane containing both magnetic vectors and both propagation directions  (i.e., the plane normal to the electric vectors).

Malus's choice

Polarization was discovered — but not named or understood — by Christiaan Huygens, as he investigated the double refraction of "Iceland crystal" (transparent calcite, now called Iceland spar). The essence of his discovery, published in his ''Treatise on Light'' (1690), was as follows. When a ray (meaning a narrow beam of light) passes through two similarly oriented calcite crystals at normal incidence, the ordinary ray emerging from the first crystal suffers only the ordinary refraction in the second, while the extraordinary ray emerging from the first suffers only the extraordinary refraction in the second. But when the second crystal is rotated 90° about the incident rays, the roles are interchanged, so that the ordinary ray emerging from the first crystal suffers only the extraordinary refraction in the second, and vice versa. At intermediate positions of the second crystal, each ray emerging from the first is doubly refracted by the second, giving four rays in total; and as the crystal is rotated from the initial orientation to the perpendicular one, the brightnesses of the rays vary, giving a smooth transition between the extreme cases in which there are only two final rays.

Huygens defined a ''principal section'' of a calcite crystal as a plane normal to a natural surface and parallel to the axis of the obtuse solid angle. This axis was parallel to the axes of the spheroidal secondary waves by which he (correctly) explained the directions of the extraordinary refraction.

The term ''polarization'' was coined by Étienne-Louis Malus in 1811.  In 1808, in the midst of confirming Huygens' geometric description of double refraction (while disputing his physical explanation), Malus had discovered that when a ray of light is reflected off a non-metallic surface at the appropriate angle, it behaves like ''one'' of the two rays emerging from a calcite crystal.The angle of reflection at which this modification occurs became known as '' Brewster's angle'', after its dependence on the refractive index was determined experimentally by David Brewster in 1815. As this behavior had previously been known only in connection with double refraction, Malus described it in that context. In particular, he defined the ''plane of polarization'' of a polarized ray as the plane, containing the ray, in which a principal section of a calcite crystal must lie in order to cause only ''ordinary'' refraction. This definition was all the more reasonable because it meant that when a ray was polarized by reflection (off an isotopic medium), the plane of polarization was the plane of incidence and reflection — that is, the plane containing the incident ray, the normal to the reflective surface, and the polarized reflected ray. But, as we now know, this plane happens to contain the ''magnetic'' vectors of the polarized ray, not the electric vectors.

The plane of the ray and the magnetic vectors is the one numbered (2b) above. The implication that the plane of polarization contains the ''magnetic'' vectors is still found in the definition given in the online Merriam-Webster dictionary. Even Julius Adams Stratton, having said that "It is customary to define the polarization in terms of E", promptly adds: "In optics, however, the orientation of the vectors is specified traditionally by the 'plane of polarization,' by which is meant the plane normal to E containing both H and the axis of propagation." That definition is identical with Malus's.

Fresnel's choice

In 1821, Augustin-Jean Fresnel announced his hypothesis that light waves are exclusively ''transverse'' and therefore ''always'' polarized in the sense of having a particular transverse orientation, and that what we call '' unpolarized light'' is in fact light whose orientation is rapidly and randomly changing.A. Fresnel, "Note sur le calcul des teintes que la polarisation développe dans les lames cristallisées" et seq., ''Annales de Chimie et de Physique'', Ser. 2, vol. 17, pp. 102–11 (May 1821), 167–96 (June 1821), 312–15 ("Postscript", July 1821); reprinted (with added section nos.) in H. de Sénarmont, E. Verdet, and L. Fresnel (eds.), ''Oeuvres complètes d'Augustin Fresnel'', vol. 1 (1866), pp. 609–48; translated as "On the calculation of the tints that polarization develops in crystalline plates, & postscript", (Creative Commons), 2021. Supposing that light waves were analogous to shear waves in elastic solids, and that a higher refractive index corresponded to a higher density of the luminiferous aether, he found that he could account for the partial reflection (including polarization by reflection) at the interface between two transparent isotropic media, provided that the vibrations of the aether were perpendicular to the plane of polarization. Thus the polarization, according to the received definition, was "in" a certain plane if the vibrations were ''perpendicular'' to that plane!

Fresnel himself found this implication inconvenient; later that year he wrote:
::Adopting this hypothesis, it would have been more natural to have called the plane of polarisation that in which the oscillations are supposed to be made: but I wished to avoid making any change in the received appellations.The actual writing of this treatise (Fresnel, 1822) was apparently completed by mid 1821; see I. Grattan-Guinness, ''Convolutions in French Mathematics, 1800–1840'', Basel: Birkhäuser, 1990, vol.2, p.884.
But he soon felt obliged to make a less radical change. In his successful model of double refraction, the displacement of the medium was constrained to be tangential to the wavefront, while the force was allowed to deviate from the displacement and from the wavefront. Hence, if the vibrations were perpendicular to the plane of polarization, then the plane of polarization contained the wave-normal but not necessarily the ray. In his "Second Memoir" on double refraction, Fresnel formally adopted this new definition, acknowledging that it agreed with the old definition in an isotropic medium such as air, but not in a birefringent crystal.

The vibrations normal to Malus's plane of polarization are electric, and the electric vibration tangential to the wavefront is D (Fig.1). Thus, in terms of the above numbering, Fresnel changed the "plane of polarization" from (2b) to (2a). Fresnel's definition remains compatible with the Merriam-Webster definition, which fails to specify the propagation direction. And it remains compatible with Stratton's definition, because that is given in the context of an isotropic medium, in which planes (2a) and (2b) merge into (2).

What Fresnel called the "more natural" choice was a plane containing D and a direction of propagation. In Fig.1, the only plane meeting that specification is the one labeled "Plane of vibration" and later numbered (1) — that is, the one that ''modern'' authors tend to identify with the "plane of polarization". We might therefore wish that Fresnel had been less deferential to his predecessors. That scenario, however, is less realistic than it may seem, because even after Fresnel's transverse-wave theory was generally accepted, the direction of the vibrations was the subject of continuing debate.

"Plane of vibration"

The principle that refractive index depended on the density of the aether was essential to Fresnel's aether drag hypothesis. But it could not be extended to birefringent crystals — in which at least one refractive index varies with direction — because density is not directional. Hence his explanation of refraction required a directional variation in stiffness of the aether ''within'' a birefringent medium, plus a variation in density ''between'' media.

James MacCullagh and Franz Ernst Neumann avoided this complication by supposing that a higher refractive index corresponded always to the same density but a greater elastic ''compliance'' (lower stiffness). To obtain results that agreed with observations on partial reflection, they had to suppose, contrary to Fresnel, that the vibrations were ''within'' the plane of polarization.

The question called for an experimental determination of the direction of vibration, and the challenge was answered by George Gabriel Stokes. He defined the ''plane of vibration'' as "the plane passing through the ray and the direction of vibration" (in agreement with Fig.1). Now suppose that a fine diffraction grating is illuminated at normal incidence. At large angles of diffraction, the grating will appear somewhat edge-on, so that the directions of vibration will be crowded towards the direction parallel to the plane of the grating. If the planes of polarization coincide with the planes of vibration (as MacCullagh and Neumann said), they will be crowded in the same direction; and if the planes of polarization are ''normal'' to the planes of vibration (as Fresnel said), the planes of polarization will be crowded in the normal direction. To find the direction of the crowding, one could vary the polarization of the incident light in equal steps, and determine the planes of polarization of the diffracted light in the usual manner. Stokes performed such an experiment in 1849, and it found in favor of Fresnel.

In 1852, Stokes noted a much simpler experiment that leads to the same conclusion. Sunlight scattered from a patch of blue sky 90° from the sun is found, by the methods of Malus, to be polarized in the plane containing the line of sight and the sun. But it is obvious from the geometry that the vibrations of that light can only be perpendicular to that plane.

There was, however, a sense in which MacCullagh and Neumann were correct. If we attempt an analogy between shear waves in a non-isotropic elastic solid, and EM waves in a magnetically isotropic but electrically non-isotropic crystal, the density must correspond to the magnetic permeability (both being non-directional), and the compliance must correspond to the electric permittivity (both being directional). The result is that the velocity of the solid corresponds to the H field, so that the mechanical vibrations of the shear wave are in the direction of the ''magnetic'' vibrations of the EM wave. But Stokes's experiments were bound to detect the ''electric'' vibrations, because those have the greater propensity to interact with matter. In short, the MacCullagh-Neumann vibrations were the ones that had a mechanical analog, but Fresnel's vibrations were the ones that were more likely to be detected in experiments.Concerning the limitations of elastic-electromagnetic analogies, see (e.g.) Born & Wolf, 1970, pp.xxiv–xxv; Darrigol, 2012, pp.227–32.

Modern practice

The electromagnetic theory of light further emphasized the ''electric'' vibrations because of their interactions with matter, whereas the old "plane of polarization" contained the ''magnetic'' vectors. Hence the electromagnetic theory would have reinforced the convention that the vibrations were normal to the plane of polarization — provided, of course, that one was familiar with the historical definition of the plane of polarization. But if one was influenced by physical considerations ''alone'', then, as Feynman and the ''Britannica'' illustrate, one would pay attention to the electric vectors and assume that the "plane" of polarization (if one needed such a concept) contained those vectors.

However, it is not clear that a "plane of polarization" is needed at all: knowing what field vectors are involved, one can specify the polarization by specifying the orientation of a particular vector, or, as Born and Wolf suggest, by specifying the "plane of vibration" of that vector.  Hecht also prefers the term ''plane of vibration'' (or, more usually, ''plane-of-vibration''), which he defines as the plane of E and the wave-normal, in agreement with Fig.1 above.

Remaining uses

In an optically ''chiral'' medium — that is, one in which the direction of polarization gradually rotates as the wave propagates — the choice of definition of the "plane of polarization" does not affect the existence or direction ("handedness") of the rotation. This is one context in which the ambiguity of the term ''plane of polarization'' causes no further confusion.

There is also a context in which the original definition might still suggest itself. In a non-magnetic non-chiral crystal of the ''biaxial'' class (in which there is no ordinary refraction, but both refractions violate Snell's law), there are three mutually perpendicular planes for which the speed of light is isotropic within the plane provided that the electric vectors are normal to the plane. This situation naturally draws attention to a plane normal to the vibrations as envisaged by Fresnel, and that plane is indeed the plane of polarization as defined by Fresnel or Malus.

In most contexts, however, the concept of a "plane of polarization" distinct from a plane containing the electric "vibrations" has arguably become redundant, and has certainly become a source of confusion. In the words of Born & Wolf, "it is… better not to use this term."Born & Wolf, 1970, p.43.

See also

*E-plane and H-plane
*Plane of incidence

Notes

References

Bibliography

* W.S. Aldis, 1879
''A Chapter on Fresnel's Theory of Double Refraction''
2nd Ed., Cambridge: Deighton, Bell, & Co. / London: George Bell & Sons.
* M. Born and E. Wolf, 1970, ''Principles of Optics'', 4th Ed., Oxford: Pergamon Press.
* J.Z. Buchwald, 1989, ''The Rise of the Wave Theory of Light: Optical Theory and Experiment in the Early Nineteenth Century'', University of Chicago Press, .
* O. Darrigol, 2012, ''A History of Optics: From Greek Antiquity to the Nineteenth Century'', Oxford, .
* A. Fresnel, 1822, ''De la Lumière'' (''On Light''), in J. Riffault (ed.)
''Supplément à la traduction française de la cinquième édition du "Système de Chimie" par Th.Thomson''
Paris: Chez Méquignon-Marvis, 1822, pp.1–137,535–9; reprinted in Fresnel, 1866–70, vol.2
pp.3–146
translated by T. Young as "Elementary view of the undulatory theory of light", ''Quarterly Journal of Science, Literature, and Art'', vol.22 (Jan.–Jun.1827), p
127–41441–54
vol.23 (Jul.–Dec.1827), p
113–35431–48
vol.24 (Jan.–Jun.1828), p
198–215
vol.25 (Jul.–Dec.1828), p
168–91389–407
vol.26 (Jan.–Jun.1829), p
159–65

* A. Fresnel, 1827, "Mémoire sur la double réfraction", ''Mémoires de l'Académie Royale des Sciences de l'Institut de France'', vol. (for 1824, printed 1827)
pp.45–176
reprinted as "Second mémoire…" in Fresnel, 1866–70, vol.2
pp.479–596
translated by A.W. Hobson a
"Memoir on double refraction"
in R.Taylor (ed.), ''Scientific Memoirs'', vol. (London: Taylor & Francis, 1852), pp.238–333. (Cited page numbers are from the translation.)
* A. Fresnel (ed. H. de Senarmont, E. Verdet, and L. Fresnel), 1866–70, ''Oeuvres complètes d'Augustin Fresnel'' (3 volumes), Paris: Imprimerie Impériale
vol.1 (1866)vol.2 (1868)vol.3 (1870)

* E. Hecht, 2017, ''Optics'', 5th Ed., Pearson Education, .
* C. Huygens, 1690, ''Traité de la Lumière'' (Leiden: Van der Aa), translated by S.P. Thompson as
Treatise on Light
', University of Chicago Press, 1912; Project Gutenberg, 2005. (Cited page numbers match the 1912 edition and the Gutenberg HTML edition.)
* B. Powell (July 1856)
"On the demonstration of Fresnel's formulas for reflected and refracted light; and their applications"
''Philosophical Magazine and Journal of Science'', Series 4, vol.12, no.76, pp.1–20.
* J.A. Stratton, 1941, ''Electromagnetic Theory'', New York: McGraw-Hill.
* E. T. Whittaker, 1910, ''A History of the Theories of Aether and Electricity: From the Age of Descartes to the Close of the Nineteenth Century'', London: Longmans, Green, & Co.

{{Authority control

Light
Optics
Physical optics
Polarization (waves)
Electromagnetic radiation
Antennas (radio)
History of physics
Planes (geometry)