Persistent Homology Group on:
[Wikipedia]
[Google]
[Amazon]
In persistent homology, a persistent homology group is a multiscale analog of a
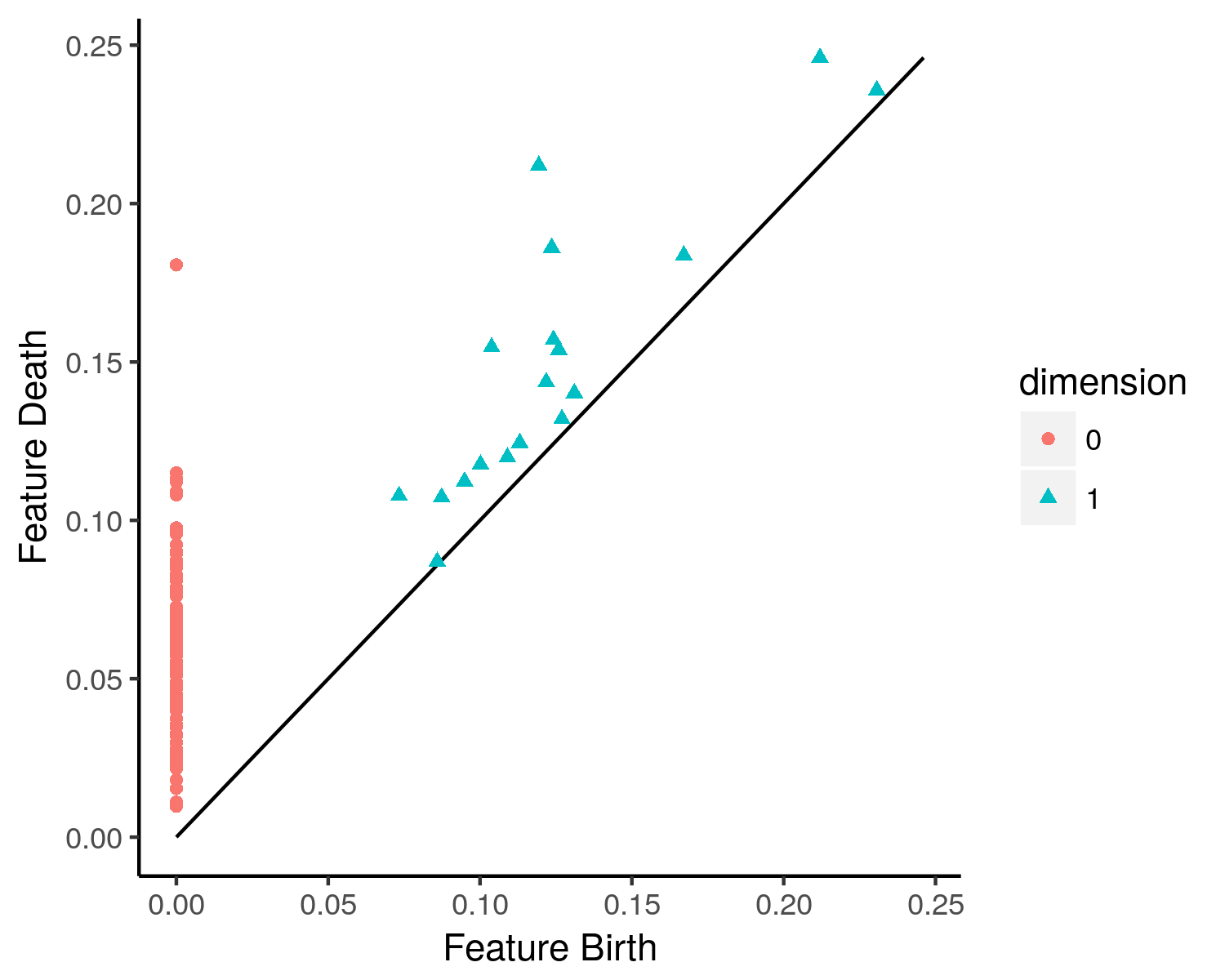 Geometrically, a barcode can be plotted as a multiset of points (with possibly infinite coordinates) in the extended plane . By the above definitions, each point will lie above the diagonal, and the distance to the diagonal is exactly equal to the persistence of the corresponding class times . This construction is known as the ''persistence diagram'', and it provides a way of visualizing the structure of the persistence of homology classes in the sequence of persistent homology groups.
Geometrically, a barcode can be plotted as a multiset of points (with possibly infinite coordinates) in the extended plane . By the above definitions, each point will lie above the diagonal, and the distance to the diagonal is exactly equal to the persistence of the corresponding class times . This construction is known as the ''persistence diagram'', and it provides a way of visualizing the structure of the persistence of homology classes in the sequence of persistent homology groups.
homology group
In mathematics, the term homology, originally introduced in algebraic topology, has three primary, closely-related usages. The most direct usage of the term is to take the ''homology of a chain complex'', resulting in a sequence of abelian grou ...
that captures information about the evolution of topological features across a filtration
Filtration is a physical separation process that separates solid matter and fluid from a mixture using a ''filter medium'' that has a complex structure through which only the fluid can pass. Solid particles that cannot pass through the filte ...
of spaces. While the ordinary homology group represents nontrivial homology classes of an individual topological space
In mathematics, a topological space is, roughly speaking, a Geometry, geometrical space in which Closeness (mathematics), closeness is defined but cannot necessarily be measured by a numeric Distance (mathematics), distance. More specifically, a to ...
, the persistent homology group tracks only those classes that remain nontrivial across multiple parameters in the underlying filtration. Analogous to the ordinary Betti number
In algebraic topology, the Betti numbers are used to distinguish topological spaces based on the connectivity of ''n''-dimensional simplicial complexes. For the most reasonable finite-dimensional spaces (such as compact manifolds, finite simplicia ...
, the ranks of the persistent homology groups are known as the persistent Betti numbers. Persistent homology groups were first introduced by Herbert Edelsbrunner, David Letscher, and Afra Zomorodian in a 2002 paper ''Topological Persistence and Simplification'', one of the foundational papers in the fields of persistent homology and topological data analysis
In applied mathematics, topological data analysis (TDA) is an approach to the analysis of datasets using techniques from topology. Extraction of information from datasets that are high-dimensional, incomplete and noisy is generally challenging. TDA ...
, based largely on the persistence barcodes and the persistence algorithm, that were first described by Serguei Barannikov in the 1994 paper. Since then, the study of persistent homology groups has led to applications in data science
Data science is an interdisciplinary academic field that uses statistics, scientific computing, scientific methods, processing, scientific visualization, algorithms and systems to extract or extrapolate knowledge from potentially noisy, stru ...
, machine learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task ( ...
, materials science
Materials science is an interdisciplinary field of researching and discovering materials. Materials engineering is an engineering field of finding uses for materials in other fields and industries.
The intellectual origins of materials sci ...
, biology
Biology is the scientific study of life and living organisms. It is a broad natural science that encompasses a wide range of fields and unifying principles that explain the structure, function, growth, History of life, origin, evolution, and ...
, and economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and interac ...
.
Definition
Let be asimplicial complex
In mathematics, a simplicial complex is a structured Set (mathematics), set composed of Point (geometry), points, line segments, triangles, and their ''n''-dimensional counterparts, called Simplex, simplices, such that all the faces and intersec ...
, and let be a real-valued
In mathematics, value may refer to several, strongly related notions.
In general, a mathematical value may be any definite mathematical object. In elementary mathematics, this is most often a number – for example, a real number such as or an ...
monotonic function
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of or ...
. Then for some values the sublevel-sets yield a sequence of nested subcomplexes known as a ''filtration'' of .
Applying homology to each complex yields a sequence of homology groups connected by homomorphism
In algebra, a homomorphism is a morphism, structure-preserving map (mathematics), map between two algebraic structures of the same type (such as two group (mathematics), groups, two ring (mathematics), rings, or two vector spaces). The word ''homo ...
s induced by the inclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function \iota that sends each element x of A to x, treated as an element of B:
\iota : A\rightarrow B, \qquad \iota(x)=x.
An inclusion map may also be referred to as an inclu ...
s of the underlying filtration. When homology is taken over a field, we get a sequence of vector space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called sc ...
s and linear map
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that p ...
s known as a persistence module.
Let be the homomorphism induced by the inclusion . Then the persistent homology groups are defined as the images
An image or picture is a visual representation. An image can be two-dimensional, such as a drawing, painting, or photograph, or three-dimensional, such as a carving or sculpture. Images may be displayed through other media, including a project ...
for all . In particular, the persistent homology group .
More precisely, the persistent homology group can be defined as , where and are the standard p-cycle and p-boundary groups, respectively.
Birth and death of homology classes
Sometimes the elements of are described as the homology classes that are "born" at or before and that have not yet "died" entering . These notions can be made precise as follows. A homology class is said to be ''born'' at if it is not contained in the image of the previous persistent homology group, i.e., . Conversely, is said to ''die entering'' if is subsumed (i.e., merges with) another older class as the sequence proceeds from . That is to say, but . The determination that an older class persists if it merges with a younger class, instead of the other way around, is sometimes known as the ''Elder Rule''. The indices at which a homology class is born and dies entering are known as the ''birth'' and ''death'' indices of . The difference is known as the ''index persistence'' of , while the corresponding difference in function values corresponding to those indices is known as the ''persistence'' of . If there exists no index at which dies, it is assigned an infinite death index. Thus, the persistence of each class can be represented as an interval in the extended real line of either the form or . Since, in the case of an infinite field, the infinite number of classes always have the same persistence, the collection over ''all'' classes of such intervals does not give meaningful multiplicities for a multiset of intervals. Instead, such multiplicities and a multiset of intervals in the extended real line are given by the structure theorem of persistent homology, persistence homology. This multiset is known as the '' persistence barcode''.Canonical form
Concretely, the structure theorem states that for any filtered complex over a field , there exists a linear transformation that preserves the filtration and converts the filtered complex into so called canonical form, a canonically defined direct sum of filtered complexes of two types: two-dimensional complexes with trivial homology and one-dimensional complexes with trivial differential .Persistence diagram
 Geometrically, a barcode can be plotted as a multiset of points (with possibly infinite coordinates) in the extended plane . By the above definitions, each point will lie above the diagonal, and the distance to the diagonal is exactly equal to the persistence of the corresponding class times . This construction is known as the ''persistence diagram'', and it provides a way of visualizing the structure of the persistence of homology classes in the sequence of persistent homology groups.
Geometrically, a barcode can be plotted as a multiset of points (with possibly infinite coordinates) in the extended plane . By the above definitions, each point will lie above the diagonal, and the distance to the diagonal is exactly equal to the persistence of the corresponding class times . This construction is known as the ''persistence diagram'', and it provides a way of visualizing the structure of the persistence of homology classes in the sequence of persistent homology groups.
References