Pentagonal Tilings on:
[Wikipedia]
[Google]
[Amazon]
In
 A '' regular pentagon'' has
A '' regular pentagon'' has
 One method to construct a regular pentagon in a given circle is described by Richmond and further discussed in Cromwell's ''
One method to construct a regular pentagon in a given circle is described by Richmond and further discussed in Cromwell's ''
 The Carlyle circle was invented as a geometric method to find the roots of a
The Carlyle circle was invented as a geometric method to find the roots of a
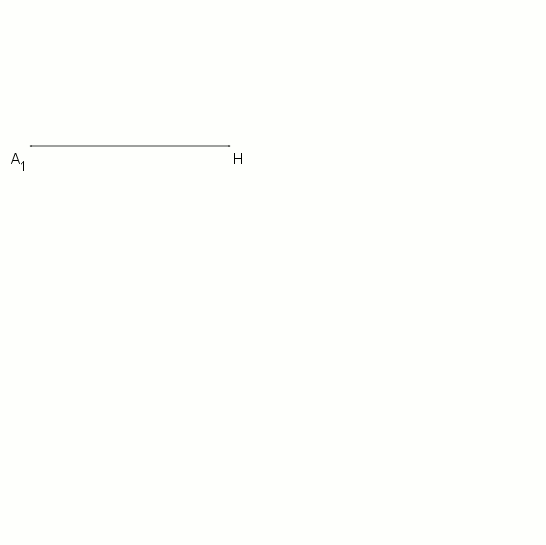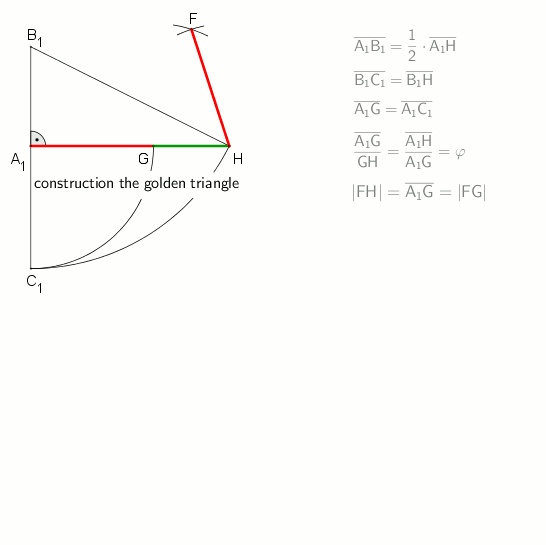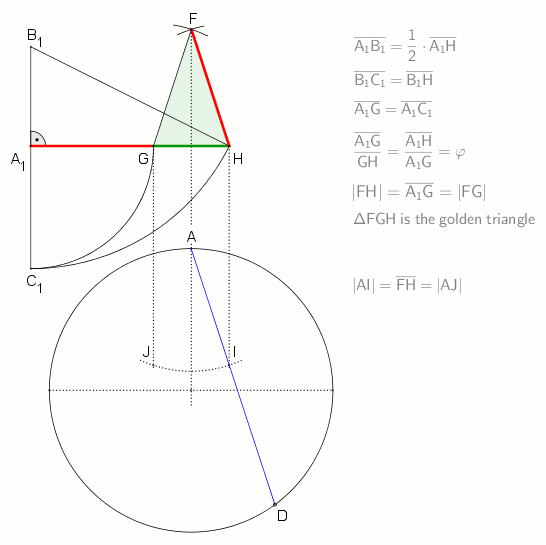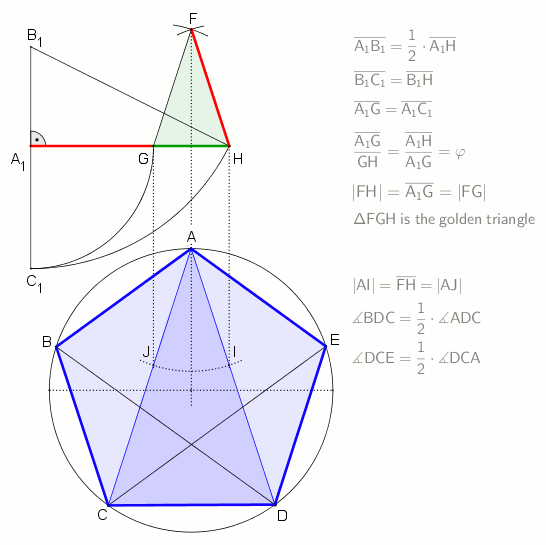 A regular pentagon is constructible using a
A regular pentagon is constructible using a
 * A regular pentagon may be created from just a strip of paper by tying an
* A regular pentagon may be created from just a strip of paper by tying an
 The ''regular pentagon'' has Dih5 symmetry, order 10. Since 5 is a
The ''regular pentagon'' has Dih5 symmetry, order 10. Since 5 is a
 An equilateral pentagon is a polygon with five sides of equal length. However, its five internal angles can take a range of sets of values, thus permitting it to form a family of pentagons. In contrast, the regular pentagon is unique
An equilateral pentagon is a polygon with five sides of equal length. However, its five internal angles can take a range of sets of values, thus permitting it to form a family of pentagons. In contrast, the regular pentagon is unique
:.
 A regular pentagon cannot appear in any tiling of regular polygons. First, to prove a pentagon cannot form a
A regular pentagon cannot appear in any tiling of regular polygons. First, to prove a pentagon cannot form a
File:BhindiCutUp.jpg, Pentagonal cross-section of
File:Oreaster reticulatus201905mx.jpg, A
File:Ho-Mg-ZnQuasicrystal.jpg, A Ho-Mg-Zn icosahedral
File:The Pentagon January 2008.jpg,
Animated demonstration
constructing an inscribed pentagon with compass and straightedge.
How to construct a regular pentagon
with only a compass and straightedge.
using only a strip of paper
with interactive animation
Renaissance artists' approximate constructions of regular pentagons
How to calculate various dimensions of regular pentagons.
{{Authority control Constructible polygons Polygons by the number of sides 5 (number) Elementary shapes
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, a pentagon () is any five-sided polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain.
The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon ...
or 5-gon. The sum of the internal angle
In geometry, an angle of a polygon is formed by two adjacent edge (geometry), sides. For a simple polygon (non-self-intersecting), regardless of whether it is Polygon#Convexity and non-convexity, convex or non-convex, this angle is called an ...
s in a simple
Simple or SIMPLE may refer to:
*Simplicity, the state or quality of being simple
Arts and entertainment
* ''Simple'' (album), by Andy Yorke, 2008, and its title track
* "Simple" (Florida Georgia Line song), 2018
* "Simple", a song by John ...
pentagon is 540°.
A pentagon may be simple or self-intersecting. A self-intersecting ''regular pentagon'' (or ''star
A star is a luminous spheroid of plasma (physics), plasma held together by Self-gravitation, self-gravity. The List of nearest stars and brown dwarfs, nearest star to Earth is the Sun. Many other stars are visible to the naked eye at night sk ...
pentagon'') is called a pentagram
A pentagram (sometimes known as a pentalpha, pentangle, or star pentagon) is a regular five-pointed star polygon, formed from the diagonal line segments of a convex (or simple, or non-self-intersecting) regular pentagon. Drawing a circle around ...
.
Regular pentagons
Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines List of regular polytopes and compounds, regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, wh ...
and interior angle
In geometry, an angle of a polygon is formed by two adjacent sides. For a simple polygon (non-self-intersecting), regardless of whether it is convex or non-convex, this angle is called an internal angle (or interior angle) if a point withi ...
s of 108°.
A '' regular pentagon'' has five lines of reflectional symmetry
In mathematics, reflection symmetry, line symmetry, mirror symmetry, or mirror-image symmetry is symmetry with respect to a reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.
In two-di ...
, and rotational symmetry
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape (geometry), shape has when it looks the same after some rotation (mathematics), rotation by a partial turn (angle), turn. An object's degree of rotational s ...
of order 5 (through 72°, 144°, 216° and 288°). The diagonal
In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word ''diagonal'' derives from the ancient Greek � ...
s of a convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytop ...
regular pentagon are in the golden ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their summation, sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if
\fr ...
to its sides. Given its side length its height (distance from one side to the opposite vertex), width (distance between two farthest separated points, which equals the diagonal length ) and circumradius are given by:
:
The area of a convex regular pentagon with side length is given by
:
If the circumradius of a regular pentagon is given, its edge length is found by the expression
:
and its area is
:
since the area of the circumscribed circle is the regular pentagon fills approximately 0.7568 of its circumscribed circle.
Derivation of the area formula
The area of any regular polygon is: : where ''P'' is the perimeter of the polygon, and ''r'' is theinradius
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is a triangle center called the triangle's incenter. ...
(equivalently the apothem
The apothem (sometimes abbreviated as apo) of a regular polygon is a line segment from the center to the midpoint of one of its sides. Equivalently, it is the line drawn from the center of the polygon that is perpendicular to one of its sides. T ...
). Substituting the regular pentagon's values for ''P'' and ''r'' gives the formula
:
with side length ''t''.
Inradius
Similar to every regular convex polygon, the regular convex pentagon has aninscribed circle
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is a triangle center called the triangle's incente ...
. The apothem
The apothem (sometimes abbreviated as apo) of a regular polygon is a line segment from the center to the midpoint of one of its sides. Equivalently, it is the line drawn from the center of the polygon that is perpendicular to one of its sides. T ...
, which is the radius ''r'' of the inscribed circle, of a regular pentagon is related to the side length ''t'' by
:
Chords from the circumscribed circle to the vertices
Like every regular convex polygon, the regular convex pentagon has acircumscribed circle In geometry, a circumscribed circle for a set of points is a circle passing through each of them. Such a circle is said to ''circumscribe'' the points or a polygon formed from them; such a polygon is said to be ''inscribed'' in the circle.
* Circu ...
. For a regular pentagon with successive vertices A, B, C, D, E, if P is any point on the circumcircle between points B and C, then PA + PD = PB + PC + PE.
Point in plane
For an arbitrary point in the plane of a regular pentagon with circumradius , whose distances to the centroid of the regular pentagon and its five vertices are and respectively, we have : If are the distances from the vertices of a regular pentagon to any point on its circumcircle, then :Geometrical constructions
The regular pentagon is constructible withcompass and straightedge
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an Idealiz ...
, as 5 is a Fermat prime
In mathematics, a Fermat number, named after Pierre de Fermat (1601–1665), the first known to have studied them, is a positive integer of the form:F_ = 2^ + 1, where ''n'' is a non-negative integer. The first few Fermat numbers are: 3, 5, ...
. A variety of methods are known for constructing a regular pentagon. Some are discussed below.
Richmond's method
Polyhedra
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices. The term "polyhedron" may refer either to a solid figure or to its boundary su ...
''.
The top panel shows the construction used in Richmond's method to create the side of the inscribed pentagon. The circle defining the pentagon has unit radius. Its center is located at point ''C'' and a midpoint ''M'' is marked halfway along its radius. This point is joined to the periphery vertically above the center at point ''D''. Angle ''CMD'' is bisected, and the bisector intersects the vertical axis at point ''Q''. A horizontal line through ''Q'' intersects the circle at point ''P'', and chord ''PD'' is the required side of the inscribed pentagon.
To determine the length of this side, the two right triangles ''DCM'' and ''QCM'' are depicted below the circle. Using Pythagoras' theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite ...
and two sides, the hypotenuse of the larger triangle is found as . Side ''h'' of the smaller triangle then is found using the half-angle formula
In trigonometry, trigonometric identities are Equality (mathematics), equalities that involve trigonometric functions and are true for every value of the occurring Variable (mathematics), variables for which both sides of the equality are defined. ...
:
:
where cosine and sine of ''ϕ'' are known from the larger triangle. The result is:
:
If DP is truly the side of a regular pentagon, , so DP = 2 cos(54°), QD = DP cos(54°) = 2cos2(54°), and CQ = 1 − 2cos2(54°), which equals −cos(108°) by the cosine double angle formula
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...
. This is the cosine of 72°, which equals as desired.
Carlyle circles
 The Carlyle circle was invented as a geometric method to find the roots of a
The Carlyle circle was invented as a geometric method to find the roots of a quadratic equation
In mathematics, a quadratic equation () is an equation that can be rearranged in standard form as
ax^2 + bx + c = 0\,,
where the variable (mathematics), variable represents an unknown number, and , , and represent known numbers, where . (If and ...
. This methodology leads to a procedure for constructing a regular pentagon. The steps are as follows:
# Draw a circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
in which to inscribe the pentagon and mark the center point ''O''.
# Draw a horizontal line through the center of the circle. Mark the left intersection with the circle as point ''B''.
# Construct a vertical line through the center. Mark one intersection with the circle as point ''A''.
# Construct the point ''M'' as the midpoint of ''O'' and ''B''.
# Draw a circle centered at ''M'' through the point ''A''. Mark its intersection with the horizontal line (inside the original circle) as the point ''W'' and its intersection outside the circle as the point ''V''.
# Draw a circle of radius ''OA'' and center ''W''. It intersects the original circle at two of the vertices of the pentagon.
# Draw a circle of radius ''OA'' and center ''V''. It intersects the original circle at two of the vertices of the pentagon.
# The fifth vertex is the rightmost intersection of the horizontal line with the original circle.
Steps 6–8 are equivalent to the following version, shown in the animation:
: 6a. Construct point F as the midpoint of O and W.
: 7a. Construct a vertical line through F. It intersects the original circle at two of the vertices of the pentagon. The third vertex is the rightmost intersection of the horizontal line with the original circle.
: 8a. Construct the other two vertices using the compass and the length of the vertex found in step 7a.
Euclid's method
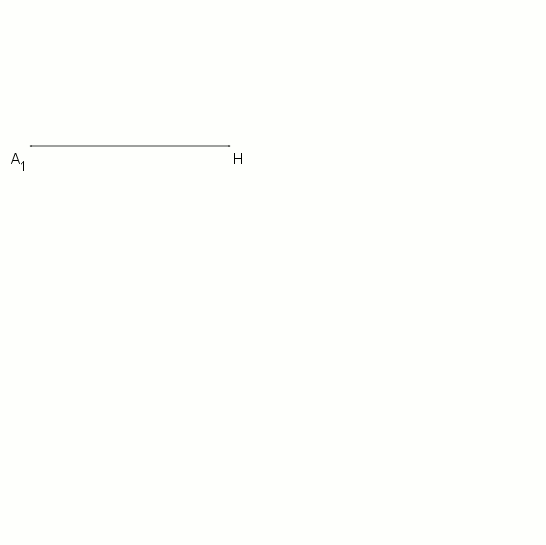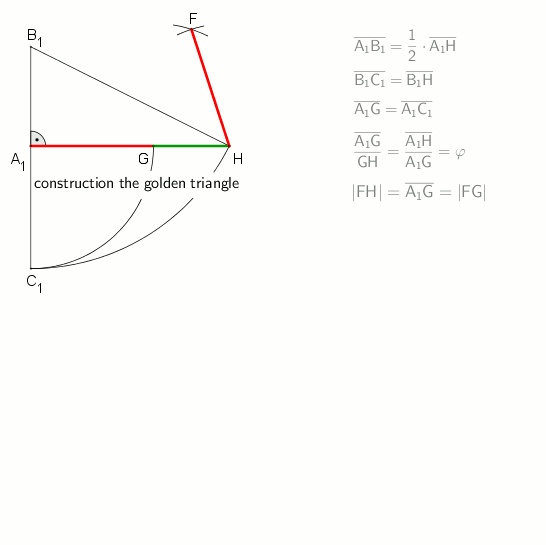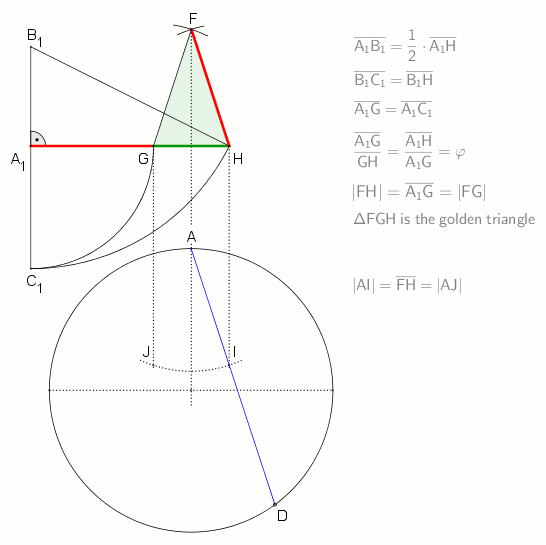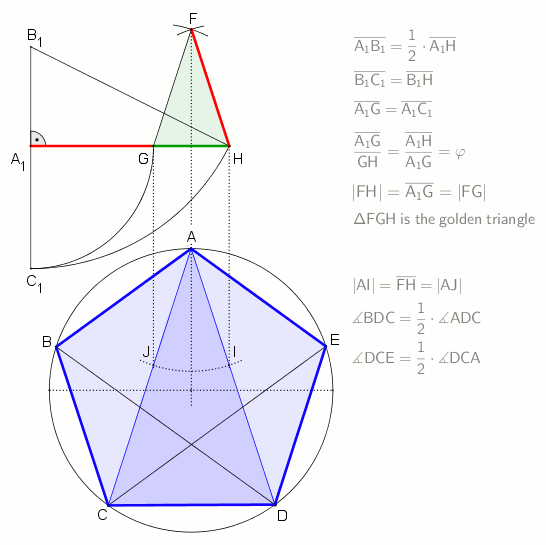 A regular pentagon is constructible using a
A regular pentagon is constructible using a compass and straightedge
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an Idealiz ...
, either by inscribing one in a given circle or constructing one on a given edge. This process was described by Euclid
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely domina ...
in his '' Elements'' circa 300 BC.
Physical construction methods
overhand knot
The overhand knot is one of the most fundamental knots, and it forms the basis of many others, including the simple noose, overhand loop, angler's loop, reef knot, fisherman's knot, half hitch, and water knot. The overhand knot is a stoppe ...
into the strip and carefully flattening the knot by pulling the ends of the paper strip. Folding one of the ends back over the pentagon will reveal a pentagram
A pentagram (sometimes known as a pentalpha, pentangle, or star pentagon) is a regular five-pointed star polygon, formed from the diagonal line segments of a convex (or simple, or non-self-intersecting) regular pentagon. Drawing a circle around ...
when backlit.
* Construct a regular hexagon
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
Regular hexagon
A regular hexagon is de ...
on stiff paper or card. Crease along the three diameters between opposite vertices. Cut from one vertex to the center to make an equilateral triangular flap. Fix this flap underneath its neighbor to make a pentagonal pyramid
In geometry, a pentagonal pyramid is a Pyramid (geometry), pyramid with a pentagon base and five triangular faces, having a total of six faces. It is categorized as a Johnson solid if all of the edges are equal in length, forming Equilateral tria ...
. The base of the pyramid is a regular pentagon.
Symmetry
 The ''regular pentagon'' has Dih5 symmetry, order 10. Since 5 is a
The ''regular pentagon'' has Dih5 symmetry, order 10. Since 5 is a prime number
A prime number (or a prime) is a natural number greater than 1 that is not a Product (mathematics), product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime ...
, there is one subgroup with dihedral symmetry: Dih1, and 2 cyclic group
In abstract algebra, a cyclic group or monogenous group is a Group (mathematics), group, denoted C_n (also frequently \Z_n or Z_n, not to be confused with the commutative ring of P-adic number, -adic numbers), that is Generating set of a group, ge ...
symmetries: Z5, and Z1.
These 4 symmetries can be seen in 4 distinct symmetries on the pentagon. John Conway labels these by a letter and group order. Full symmetry of the regular form is r10 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g5 subgroup has no degrees of freedom but can be seen as directed edges.
Regular pentagram
A pentagram or pentangle is a regularstar
A star is a luminous spheroid of plasma (physics), plasma held together by Self-gravitation, self-gravity. The List of nearest stars and brown dwarfs, nearest star to Earth is the Sun. Many other stars are visible to the naked eye at night sk ...
pentagon. Its Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines List of regular polytopes and compounds, regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, wh ...
is . Its sides form the diagonals of a regular convex pentagon – in this arrangement the sides of the two pentagons are in the golden ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their summation, sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if
\fr ...
.
Equilateral pentagons
up to Two Mathematical object, mathematical objects and are called "equal up to an equivalence relation "
* if and are related by , that is,
* if holds, that is,
* if the equivalence classes of and with respect to are equal.
This figure of speech ...
similarity, because it is equilateral and it is equiangular (its five angles are equal).
Cyclic pentagons
A cyclic pentagon is one for which a circle called the circumcircle goes through all five vertices. The regular pentagon is an example of a cyclic pentagon. The area of a cyclic pentagon, whether regular or not, can be expressed as one fourth the square root of one of the roots of aseptic equation
In algebra, a septic equation is an equation of the form
:ax^7+bx^6+cx^5+dx^4+ex^3+fx^2+gx+h=0,\,
where .
A septic function is a function of the form
:f(x)=ax^7+bx^6+cx^5+dx^4+ex^3+fx^2+gx+h\,
where . In other words, it is a polynomial of ...
whose coefficients are functions of the sides of the pentagon.
There exist cyclic pentagons with rational sides and rational area; these are called Robbins pentagons. It has been proven that the diagonals of a Robbins pentagon must be either all rational or all irrational, and it is conjectured that all the diagonals must be rational.
General convex pentagons
For all convex pentagons with sides and diagonals , the following inequality holds:''Inequalities proposed in “Crux Mathematicorum
''Crux Mathematicorum'' is a scientific journal of mathematics published by the Canadian Mathematical Society. It contains mathematical problems for secondary school and undergraduate students. Its editor-in-chief is Kseniya Garaschuk.
The journ ...
”'':.
Pentagons in tiling
regular tiling
Euclidean Plane (mathematics), plane Tessellation, tilings by convex regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Johannes Kepler, Kepler in his (Latin language, Latin: ''The Har ...
(one in which all faces are congruent, thus requiring that all the polygons be pentagons), observe that (where 108° Is the interior angle), which is not a whole number; hence there exists no integer number of pentagons sharing a single vertex and leaving no gaps between them. More difficult is proving a pentagon cannot be in any edge-to-edge tiling made by regular polygons:
The maximum known packing density
A packing density or packing fraction of a packing in some space is the fraction of the space filled by the figures making up the packing. In simplest terms, this is the ratio of the volume of bodies in a space to the volume of the space itself. ...
of a regular pentagon is , achieved by the double lattice packing shown. In a preprint released in 2016, Thomas Hales and Wöden Kusner announced a proof that this double lattice packing of the regular pentagon (known as the "pentagonal ice-ray" Chinese lattice design, dating from around 1900) has the optimal density among all packings of regular pentagons in the plane.
There are no combinations of regular polygons with 4 or more meeting at a vertex that contain a pentagon. For combinations with 3, if 3 polygons meet at a vertex and one has an odd number of sides, the other 2 must be congruent. The reason for this is that the polygons that touch the edges of the pentagon must alternate around the pentagon, which is impossible because of the pentagon's odd number of sides. For the pentagon, this results in a polygon whose angles are all . To find the number of sides this polygon has, the result is , which is not a whole number. Therefore, a pentagon cannot appear in any tiling made by regular polygons.
There are 15 classes of pentagons that can monohedrally tile the plane. None of the pentagons have any symmetry in general, although some have special cases with mirror symmetry.
Pentagons in polyhedra
Pentagons in nature
Plants
okra
Okra (, ), ''Abelmoschus esculentus'', known in some English-speaking countries as lady's fingers, is a flowering plant in the Malvaceae, mallow family native to East Africa. Cultivated in tropical, subtropical, and warm temperate regions aro ...
.
File:Morning Glory Flower.jpg, Morning glories
Morning glory (also written as morning-glory) is the common name for over 1,000 species of flowering plants in the family Convolvulaceae, whose taxonomy and systematics remain in flux. These species are distributed across numerous genera, inc ...
, like many other flowers, have a pentagonal shape.
File:Rafflesia arnoldi - panoramio.jpg, Perigone tube of ''Rafflesia
''Rafflesia'' (), or stinking corpse lily, is a genus of Parasitic plants, parasitic flowering plants in the family Rafflesiaceae. The species have enormous flowers, the buds rising from the ground or directly from the lower stems of their host p ...
'' flower.
File:Sterappel dwarsdrsn.jpg, The gynoecium
Gynoecium (; ; : gynoecia) is most commonly used as a collective term for the parts of a flower that produce ovules and ultimately develop into the fruit and seeds. The gynoecium is the innermost whorl (botany), whorl of a flower; it consists ...
of an apple
An apple is a round, edible fruit produced by an apple tree (''Malus'' spp.). Fruit trees of the orchard or domestic apple (''Malus domestica''), the most widely grown in the genus, are agriculture, cultivated worldwide. The tree originated ...
contains five carpels, arranged in a five-pointed star
A five-pointed star (☆), geometrically an equilateral concave decagon, is a common ideogram in modern culture.
Comparatively rare in classical heraldry, it was notably introduced for the flag of the United States in the Flag Act of 1777 and si ...
File:Carambola Starfruit.jpg, Starfruit
Carambola, also known as star fruit, is the fruit of ''Averrhoa carambola'', a species of tree native to tropical Southeast Asia. The edible fruit has distinctive ridges running down its sides (usually 5–6). When cut in cross-section, it res ...
is another fruit with fivefold symmetry.
Animals
sea star
Starfish or sea stars are Star polygon, star-shaped echinoderms belonging to the class (biology), class Asteroidea (). Common usage frequently finds these names being also applied to brittle star, ophiuroids, which are correctly referred to ...
. Many echinoderms
An echinoderm () is any animal of the phylum Echinodermata (), which includes starfish, brittle stars, sea urchins, sand dollars and sea cucumbers, as well as the sessile sea lilies or "stone lilies". While bilaterally symmetrical as larv ...
have fivefold radial symmetry.
File:Sea Urchin Endoskeleton.jpg, Another example of echinoderm, a sea urchin
Sea urchins or urchins () are echinoderms in the class (biology), class Echinoidea. About 950 species live on the seabed, inhabiting all oceans and depth zones from the intertidal zone to deep seas of . They typically have a globular body cove ...
endoskeleton.
File:Haeckel Ophiodea.jpg, An illustration of brittle stars
Brittle stars, serpent stars, or ophiuroids (; ; referring to the serpent-like arms of the brittle star) are echinoderms in the class Ophiuroidea, closely related to starfish. They crawl across the sea floor using their flexible arms for locomot ...
, also echinoderms with a pentagonal shape.
Minerals
quasicrystal
A quasiperiodicity, quasiperiodic crystal, or quasicrystal, is a structure that is Order and disorder (physics), ordered but not Bravais lattice, periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks trans ...
formed as a pentagonal dodecahedron
In geometry, a dodecahedron (; ) or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three Kepler–Po ...
. The faces are true regular pentagons.
File:Pyrite elbe.jpg, A pyritohedral crystal of pyrite
The mineral pyrite ( ), or iron pyrite, also known as fool's gold, is an iron sulfide with the chemical formula Fe S2 (iron (II) disulfide). Pyrite is the most abundant sulfide mineral.
Pyrite's metallic luster and pale brass-yellow hue ...
. A pyritohedron has 12 identical pentagonal faces that are not constrained to be regular.
File:Au-Gold-2-1-16 Miass 2018-03-01 11-05-41 V3.gif, A Fiveling
A fiveling, also known as a decahedral nanoparticle, a multiply-twinned particle (MTP), a pentagonal nanoparticle, a pentatwin, or a five-fold twin is a type of twinned crystal that can exist at sizes ranging from nanometers to millimetres. It ...
of gold, half a centimeter tall.
Other examples
The Pentagon
The Pentagon is the headquarters building of the United States Department of Defense, in Arlington County, Virginia, across the Potomac River from Washington, D.C. The building was constructed on an accelerated schedule during World War II. As ...
, headquarters of the United States Department of Defense
The United States Department of Defense (DoD, USDOD, or DOD) is an United States federal executive departments, executive department of the federal government of the United States, U.S. federal government charged with coordinating and superv ...
.
File:Home base of baseball field in Třebíč, Třebíč District.jpg, Home plate
A baseball field, also called a ball field or baseball diamond, is the field upon which the game of baseball is played. The term can also be used as a metonym for a baseball park. The term sandlot is sometimes used, although this usually refers ...
of a baseball field
A baseball field, also called a ball field or baseball diamond, is the field upon which the game of baseball is played. The term can also be used as a metonym for a baseball park. The term sandlot is sometimes used, although this usually refer ...
See also
* Associahedron; A pentagon is an order-4 associahedron *Dodecahedron
In geometry, a dodecahedron (; ) or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three Kepler–Po ...
, a polyhedron whose regular form is composed of 12 pentagonal faces
* Golden ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their summation, sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if
\fr ...
* List of geometric shapes
Lists of shapes cover different types of geometry, geometric shape and related topics. They include mathematics topics and other lists of shapes, such as shapes used by drawing or teaching tools.
Mathematics
* List of mathematical shapes
* List ...
* Pentagonal number
A pentagonal number is a figurate number that extends the concept of triangular number, triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotational ...
s
* Pentagram
A pentagram (sometimes known as a pentalpha, pentangle, or star pentagon) is a regular five-pointed star polygon, formed from the diagonal line segments of a convex (or simple, or non-self-intersecting) regular pentagon. Drawing a circle around ...
* Pentagram map
* Pentastar
The Chrysler Pentastar engine family is a series of aluminium ( die-cast cylinder block) dual overhead cam 24-valve gasoline
Gasoline ( North American English) or petrol ( Commonwealth English) is a petrochemical product characterized ...
, the Chrysler logo
* Pythagoras' theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite ...
* Trigonometric constants for a pentagon
In-line notes and references
External links
*Animated demonstration
constructing an inscribed pentagon with compass and straightedge.
How to construct a regular pentagon
with only a compass and straightedge.
using only a strip of paper
with interactive animation
Renaissance artists' approximate constructions of regular pentagons
How to calculate various dimensions of regular pentagons.
{{Authority control Constructible polygons Polygons by the number of sides 5 (number) Elementary shapes