|
Apothem
The apothem (sometimes abbreviated as apo) of a regular polygon is a line segment from the center to the midpoint of one of its sides. Equivalently, it is the line drawn from the center of the polygon that is perpendicular to one of its sides. The word "apothem" can also refer to the length of that line segment and comes from the ancient Greek ''ἀπόθεμα'' ("put away, put aside"), made of ''ἀπό'' ("off, away") and ''θέμα'' ("that which is laid down"), indicating a generic line written down. Regular polygons are the only polygons that have apothems. Because of this, all the apothems in a polygon will be congruent. Properties of apothems The apothem ''a'' can be used to find the area of any regular ''n''-sided polygon of side length ''s'' according to the following formula, which also states that the area is equal to the apothem multiplied by half the perimeter since ''ns'' = ''p''. :A = \frac = \frac. This formula can be derived by partitioning the ''n' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex polygon, convex'' or ''star polygon, star''. In the limit (mathematics), limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon (effectively a Line (geometry), straight line), if the edge length is fixed. General properties These properties apply to all regular polygons, whether convex or star polygon, star: *A regular ''n''-sided polygon has rotational symmetry of order ''n''. *All vertices of a regular polygon lie on a common circle (the circumscribed circle); i.e., they are concyclic points. That is, a regular polygon is a cyclic polygon. *Together with the property of equal-length sides, this implies that every regular polygon also h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius
In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is the line segment or distance from its center to any of its Vertex (geometry), vertices. The name comes from the Latin ''radius'', meaning ray but also the spoke of a chariot wheel.Definition of Radius at dictionary.reference.com. Accessed on 2009-08-08. The typical abbreviation and mathematical symbol for radius is ''R'' or ''r''. By extension, the diameter ''D'' is defined as twice the radius:Definition of radius at mathwords.com. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Area
Area is the measure of a region's size on a surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept). Two different regions may have the same area (as in squaring the circle); by synecdoche, "area" sometimes is used to refer to the region, as in a " polygonal area". The area of a shape can be measured by comparing the shape to squares of a fixed size. In the International System of Units (SI), the standard unit of area is the square metre (written as m2), which is the area o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain. The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon's '' vertices'' or ''corners''. An ''n''-gon is a polygon with ''n'' sides; for example, a triangle is a 3-gon. A simple polygon is one which does not intersect itself. More precisely, the only allowed intersections among the line segments that make up the polygon are the shared endpoints of consecutive segments in the polygonal chain. A simple polygon is the boundary of a region of the plane that is called a ''solid polygon''. The interior of a solid polygon is its ''body'', also known as a ''polygonal region'' or ''polygonal area''. In contexts where one is concerned only with simple and solid polygons, a ''polygon'' may refer only to a simple polygon or to a solid polygon. A polygonal chain may cross over itself, creating star polyg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
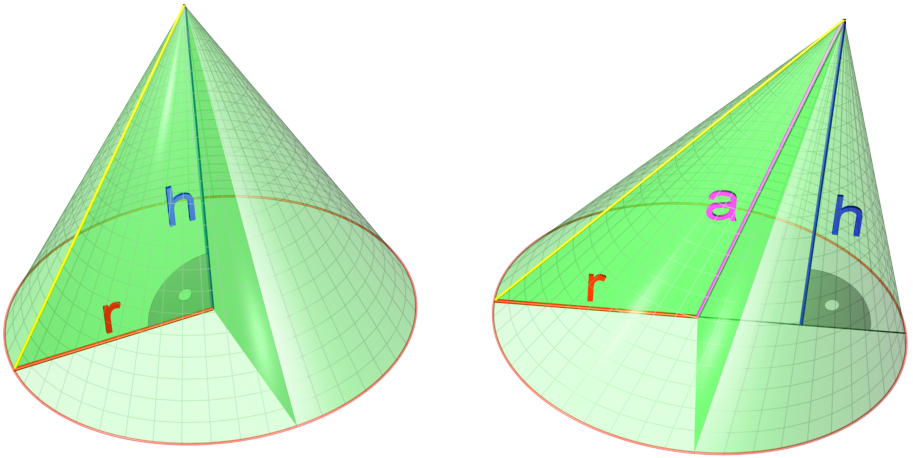
Slant Height
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the ''apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sagitta (geometry)
In geometry, the sagitta (sometimes abbreviated as sag) of a circular arc is the distance from the midpoint of the arc to the midpoint of its chord. It is used extensively in architecture when calculating the arc necessary to span a certain height and distance and also in optics where it is used to find the depth of a spherical mirror or lens. The name comes directly from Latin ''sagitta'', meaning an "arrow". Formulas In the following equations, s denotes the sagitta (the depth or height of the arc), r equals the radius of the circle, and l the length of the chord spanning the base of the arc. As \tfrac12l and r - s are two sides of a right triangle with r as the hypotenuse, the Pythagorean theorem gives us : r^2 = \left(\tfrac12l\right)^2 + \left(r-s\right)^2. This may be rearranged to give any of the other three: : \begin s &= r - \sqrt, \\ 0mul &= 2\sqrt, \\ pxr &= \frac = \frac+\frac. \end The sagitta may also be calculated from the versine function, for an arc that spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chord (trigonometry)
A chord (from the Latin ''chorda'', meaning "bowstring") of a circle is a straight line segment whose endpoints both lie on a circular arc. If a chord were to be extended Infinity, infinitely on both directions into a Line (geometry), line, the object is a ''secant line''. The perpendicular line passing through the chord's midpoint is called ''Sagitta (geometry), sagitta'' (Latin for "arrow"). More generally, a chord is a line segment joining two points on any curve, for instance, on an Ellipse#Chords, ellipse. A chord that passes through a circle's center point is the circle's ''diameter''. In circles Among properties of chords of a circle are the following: # Chords are equidistant from the center if and only if their lengths are equal. # Equal chords are subtended by equal angles from the center of the circle. # A chord that passes through the center of a circle is called a diameter and is the longest chord of that specific circle. # If the line extensions (secant lines) o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimensional line segments. A triangle has three internal angles, each one bounded by a pair of adjacent edges; the sum of angles of a triangle always equals a straight angle (180 degrees or π radians). The triangle is a plane figure and its interior is a planar region. Sometimes an arbitrary edge is chosen to be the ''base'', in which case the opposite vertex is called the ''apex''; the shortest segment between the base and apex is the ''height''. The area of a triangle equals one-half the product of height and base length. In Euclidean geometry, any two points determine a unique line segment situated within a unique straight line, and any three points that do not all lie on the same straight line determine a unique triangle situated w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inscribed Circle
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is a triangle center called the triangle's incenter. An excircle or escribed circle of the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two. Every triangle has three distinct excircles, each tangent to one of the triangle's sides. The center of the incircle, called the incenter, can be found as the intersection of the three internal angle bisectors. The center of an excircle is the intersection of the internal bisector of one angle (at vertex , for example) and the external bisectors of the other two. The center of this excircle is called the excenter relative to the vertex , or the excenter of . Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |