Numerary Nexus on:
[Wikipedia]
[Google]
[Amazon]
 In music theory and tuning, a tonality diamond is a two-dimensional diagram of
In music theory and tuning, a tonality diamond is a two-dimensional diagram of
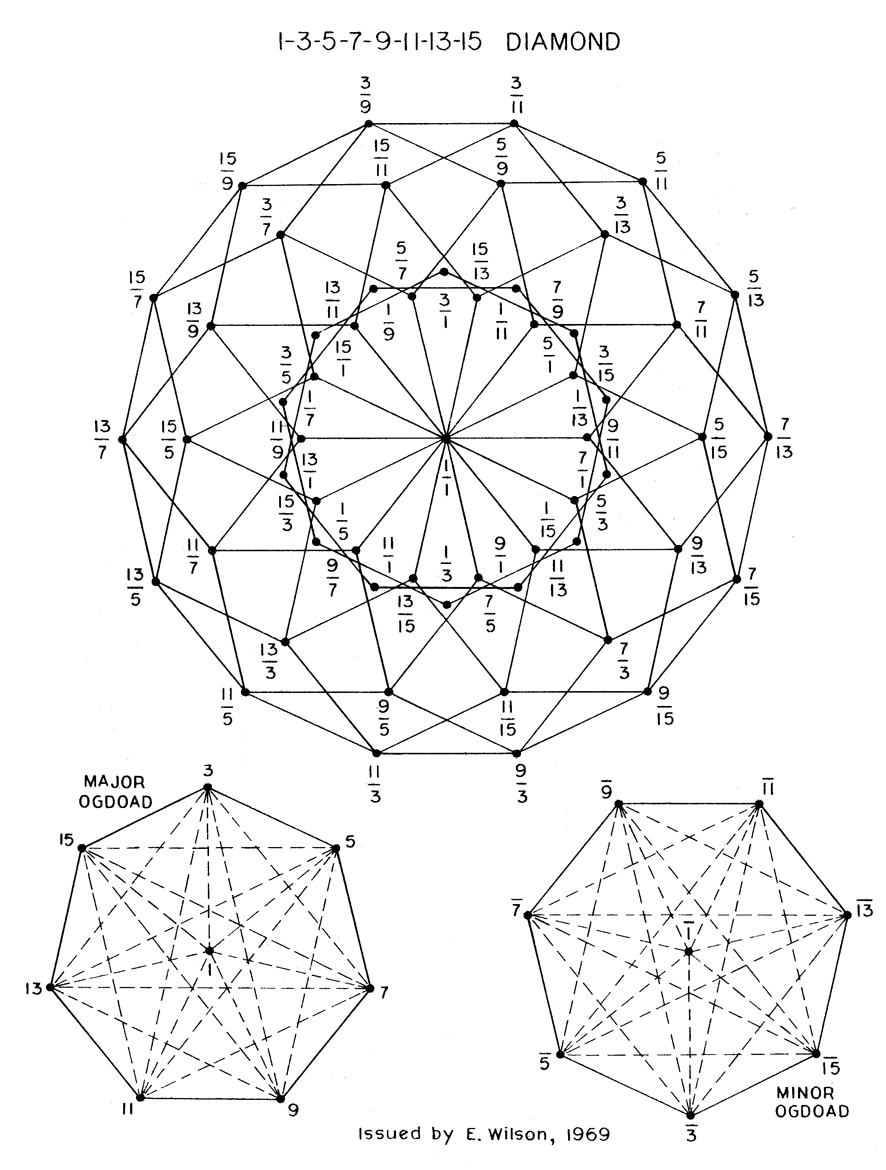
 This diamond contains six identities (1, 3, 5, 7, 9, 11). Harry Partch used the 11-limit tonality diamond, but flipped it 90 degrees.
This diamond contains six identities (1, 3, 5, 7, 9, 11). Harry Partch used the 11-limit tonality diamond, but flipped it 90 degrees.
 In music theory and tuning, a tonality diamond is a two-dimensional diagram of
In music theory and tuning, a tonality diamond is a two-dimensional diagram of ratio
In mathematics, a ratio shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
s in which one dimension is the Otonality and one the Utonality.Rasch, Rudolph (2000). "A Word or Two on the Tunings of Harry Partch", ''Harry Partch: An Anthology of Critical Perspectives'', p.28. Dunn, David, ed. . Thus the n-limit tonality diamond ("limit" here is in the sense of odd limit, not prime limit) is an arrangement in diamond-shape of the set of rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all ra ...
s ''r'', , such that the odd part of both the numerator
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight ...
and the denominator
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight ...
of ''r'', when reduced to lowest terms, is less than or equal to the fixed odd number
In mathematics, parity is the property of an integer of whether it is even or odd. An integer is even if it is a multiple of two, and odd if it is not.. For example, −4, 0, 82 are even because
\begin
-2 \cdot 2 &= -4 \\
0 \cdot 2 &= 0 \\
41 ...
''n''. Equivalently, the diamond may be considered as a set of pitch class
In music, a pitch class (p.c. or pc) is a set of all pitches that are a whole number of octaves apart; for example, the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave positi ...
es, where a pitch class is an equivalence class
In mathematics, when the elements of some set S have a notion of equivalence (formalized as an equivalence relation), then one may naturally split the set S into equivalence classes. These equivalence classes are constructed so that elements ...
of pitches under octave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been refer ...
equivalence. The tonality diamond is often regarded as comprising the set of consonances
In music, consonance and dissonance are categorizations of simultaneous or successive sounds. Within the Western tradition, some listeners associate consonance with sweetness, pleasantness, and acceptability, and dissonance with harshness, unpl ...
of the n-limit. Although originally invented by Max Friedrich Meyer
Max Friedrich Meyer (June 14, 1873 – March 14, 1967) was the first psychology professor who worked on psychoacoustics and taught at the University of Missouri. He was the founder of the theory of cochlear function, and was also an advocate ...
, the tonality diamond is now most associated with Harry Partch
Harry Partch (June 24, 1901 – September 3, 1974) was an American composer, music theorist, and creator of unique musical instruments. He composed using scales of unequal intervals in just intonation, and was one of the first 20th-century co ...
("Many theorists of just intonation consider the tonality diamond Partch's greatest contribution to microtonal theory.").
The diamond arrangement
Partch arranged the elements of the tonality diamond in the shape of arhombus
In plane Euclidean geometry, a rhombus (plural rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. Th ...
, and subdivided into (n+1)2/4 smaller rhombuses. Along the upper left side of the rhombus are placed the odd numbers from 1 to n, each reduced to the octave (divided by the minimum power of 2 such that ). These intervals are then arranged in ascending order. Along the lower left side are placed the corresponding reciprocals, 1 to 1/n, also reduced to the octave (here, ''multiplied'' by the minimum power of 2 such that ). These are placed in descending order. At all other locations are placed the product of the diagonally upper- and lower-left intervals, reduced to the octave. This gives all the elements of the tonality diamond, with some repetition. Diagonals sloping in one direction form Otonalities and the diagonals in the other direction form Utonalities. One of Partch's instruments, the diamond marimba
Harry Partch (June 24, 1901 – September 3, 1974) was an American composer, music theorist, and creator of unique musical instruments. He composed using scales of unequal intervals in just intonation, and was one of the first 20th-century com ...
, is arranged according to the tonality diamond.
Numerary nexus
A numerary nexus is an identity shared by two or moreinterval ratio
In music, an interval ratio is a ratio of the frequencies of the pitches in a musical interval. For example, a just perfect fifth (for example C to G) is 3:2 (), 1.5, and may be approximated by an equal tempered perfect fifth () which is 27/ ...
s in their numerator
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight ...
or denominator
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight ...
, with different identities in the other. For example, in the Otonality the denominator is always 1, thus 1 is the numerary nexus:
In the Utonality the numerator is always 1 and the numerary nexus is thus also 1:
For example, in a tonality diamond, such as Harry Partch
Harry Partch (June 24, 1901 – September 3, 1974) was an American composer, music theorist, and creator of unique musical instruments. He composed using scales of unequal intervals in just intonation, and was one of the first 20th-century co ...
's 11-limit diamond, each ratio of a right slanting row shares a numerator and each ratio of a left slanting row shares an denominator. Each ratio of the upper left row has 7 as a denominator, while each ratio of the upper right row has 7 (or 14) as a numerator.
5-limit
This diamond contains three identities (1, 3, 5).7-limit
This diamond contains four identities (1, 3, 5, 7).11-limit
15-limit
This diamond contains eight identities (1, 3, 5, 7, 9, 11, 13, 15).
Geometry of the tonality diamond
The five- and seven-limit tonality diamonds exhibit a highly regular geometry within themodulatory space The spaces described in this article are pitch class spaces which model the relationships between pitch classes in some musical system. These models are often graphs, groups or lattices. Closely related to pitch class space is pitch space, which ...
, meaning all non-unison elements of the diamond are only one unit from the unison. The five-limit diamond then becomes a regular hexagon
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
Regular hexagon
A ''regular hexagon'' h ...
surrounding the unison, and the seven-limit diamond a cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it ...
surrounding the unison.. Further examples of lattices of diamonds ranging from the triadic to the ogdoadic diamond have been realised by Erv Wilson
Ervin Wilson (June 11, 1928 – December 8, 2016) was a Mexican/American (dual citizen) music theorist.
Early life
Ervin Wilson was born in a remote area of northwest Chihuahua, Mexico, where he lived until the age of fifteen. His mother taught ...
where each interval is given its own unique direction.
Properties of the tonality diamond
Three properties of the tonality diamond and the ratios contained: #All ratios between neighboring ratios aresuperparticular ratio
In mathematics, a superparticular ratio, also called a superparticular number or epimoric ratio, is the ratio of two consecutive integer numbers.
More particularly, the ratio takes the form:
:\frac = 1 + \frac where is a positive integer.
Th ...
s, those with a difference of 1 between numerator
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight ...
and denominator
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight ...
.Rasch (2000), p.30.
#Ratios with relatively lower numbers have more space between them than ratios with higher numbers.
#The system, including the ratios between ratios, is symmetrical within the octave when measured in cents ''not'' in ratios.
For example:
#The ratio between and (and and ) is .
#The ratios with relatively low numbers and are 203.91 cents apart, while the ratios with relatively high numbers and are 70.67 cents apart.
#The ratio between the lowest and 2nd lowest and the highest and 2nd highest ratios are the same, and so on.
Size of the tonality diamond
If φ(''n'') isEuler's totient function
In number theory, Euler's totient function counts the positive integers up to a given integer that are relatively prime to . It is written using the Greek letter phi as \varphi(n) or \phi(n), and may also be called Euler's phi function. In ...
, which gives the number of positive integers less than n and relatively prime
In mathematics, two integers and are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them is 1. Consequently, any prime number that divides does not divide , and vice versa. This is equival ...
to n, that is, it counts the integers less than n which share no common factor with n, and if d(n) denotes the size of the n-limit tonality diamond, we have the formula
:
From this we can conclude that the rate of growth of the tonality diamond is asymptotically equal to . The first few values are the important ones, and the fact that the size of the diamond grows as the square of the size of the odd limit tells us that it becomes large fairly quickly. There are seven members to the 5-limit diamond, 13 to the 7-limit diamond, 19 to the 9-limit diamond, 29 to the 11-limit diamond, 41 to the 13-limit diamond, and 49 to the 15-limit diamond; these suffice for most purposes.
Translation to string length ratios
Yuri Landman
Yuri Landman (born 1 February 1973) is a Dutch inventor of musical instruments and musician who has made several experimental electric string instruments for a number of artists including Lee Ranaldo of Sonic Youth, Liars, Jad Fair of Half Japa ...
published an otonality and utonality diagram that clarifies the relationship of Partch's tonality diamonds to the harmonic series and string lengths (as Partch also used in his Kitharas) and Landmans Moodswinger
The Moodswinger is a twelve-string electric zither with an additional third bridge designed by Yuri Landman. The rod which functions as the third bridge divides the strings into two sections to cause an overtone multiphonic sound. One of the copie ...
instrument.http://www.hypercustom.nl/utonaldiagram.jpg
In Partch's ratios, the over number corresponds to the amount of equal divisions of a vibrating string and the under number corresponds to the which division the string length is shortened to. for example is derived from dividing the string to 5 equal parts and shortening the length to the 4th part from the bottom. In Landmans diagram these numbers is inverted, changing the frequency ratios into string length ratios.
See also
*Lattice (music)
In musical tuning, a lattice "is a way of modeling the tuning relationships of a just intonation system. It is an array of points in a periodic multidimensional pattern. Each point on the lattice corresponds to a ratio (i.e., a pitch, or an ...
* Tonality flux
References
{{DEFAULTSORT:Tonality Diamond Harry Partch Pitch space