Normalizing (abstract Rewriting) on:
[Wikipedia]
[Google]
[Amazon]
In abstract rewriting, an object is in normal form if it cannot be rewritten any further, i.e. it is irreducible. Depending on the rewriting system, an object may rewrite to several normal forms or none at all. Many properties of rewriting systems relate to normal forms.
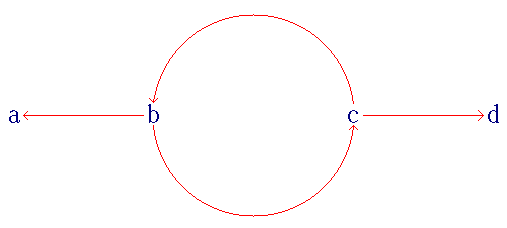 The system (pictured) is an example of a weakly normalizing but not strongly normalizing system. ''a'' and ''d'' are normal forms, and ''b'' and ''c'' can be reduced to ''a'' or ''d'', but the infinite reduction ''b'' → ''c'' → ''b'' → ''c'' → ... means that neither ''b'' nor ''c'' is strongly normalizing.
The system (pictured) is an example of a weakly normalizing but not strongly normalizing system. ''a'' and ''d'' are normal forms, and ''b'' and ''c'' can be reduced to ''a'' or ''d'', but the infinite reduction ''b'' → ''c'' → ''b'' → ''c'' → ... means that neither ''b'' nor ''c'' is strongly normalizing.
Definitions
Stated formally, if (''A'',→) is an abstract rewriting system, ''x''∈''A'' is in normal form if no ''y''∈''A'' exists such that ''x''→''y'', i.e. ''x'' is an irreducible term. An object ''a'' is weakly normalizing if there exists at least one particular sequence of rewrites starting from ''a'' that eventually yields a normal form. A rewriting system has the weak normalization property or is ''(weakly) normalizing'' (WN) if every object is weakly normalizing. An object ''a'' is strongly normalizing if every sequence of rewrites starting from ''a'' eventually terminates with a normal form. An abstract rewriting system is ''strongly normalizing'', ''terminating'', ''noetherian'', or has the (strong) normalization property (SN), if each of its objects is strongly normalizing. A rewriting system has the ''normal form property'' (NF) if for all objects ''a'' and normal forms ''b'', ''b'' can be reached from ''a'' by a series of rewrites and inverse rewrites only if ''a'' reduces to ''b''. A rewriting system has the ''unique normal form property'' (UN) if for all normal forms ''a'', ''b'' ∈ ''S'', ''a'' can be reached from ''b'' by a series of rewrites and inverse rewrites only if ''a'' is equal to ''b''. A rewriting system has the ''unique normal form property with respect to reduction'' (UN→) if for every term reducing to normal forms ''a'' and ''b'', ''a'' is equal to ''b''.Results
This section presents some well known results. First, SN implies WN.Confluence
In geography, a confluence (also: ''conflux'') occurs where two or more flowing bodies of water join to form a single channel. A confluence can occur in several configurations: at the point where a tributary joins a larger river (main stem); o ...
(abbreviated CR) implies NF implies UN implies UN→. The reverse implications do not generally hold. is UN→ but not UN as b=e and b,e are normal forms. is UN but not NF as b=c, c is a normal form, and b does not reduce to c. is NF as there are no normal forms, but not CR as a reduces to b and c, and b,c have no common reduct.
WN and UN→ imply confluence. Hence CR, NF, UN, and UN→ coincide if WN holds.
Examples
One example is that simplifying arithmetic expressions produces a number - in arithmetic, all numbers are normal forms. A remarkable fact is that all arithmetic expressions have a unique value, so the rewriting system is strongly normalizing and confluent: :(3 + 5) * (1 + 2) ⇒ 8 * (1 + 2) ⇒ 8 * 3 ⇒ 24 :(3 + 5) * (1 + 2) ⇒ (3 + 5) * 3 ⇒ 3*3 + 5*3 ⇒ 9 + 5*3 ⇒ 9 + 15 ⇒ 24 Examples of non-normalizing systems (not weakly or strongly) include counting to infinity (1 ⇒ 2 ⇒ 3 ⇒ ...) and loops such as the transformation function of the Collatz conjecture (1 ⇒ 2 ⇒ 4 ⇒ 1 ⇒ ..., it is an open problem if there are any other loops of the Collatz transformation). Another example is the single-rule system , which has no normalizing properties since from any term, e.g. ''r''(4,2) a single rewrite sequence starts, viz. ''r''(4,2) → ''r''(2,4) → ''r''(4,2) → ''r''(2,4) → ..., which is infinitely long. This leads to the idea of rewriting "modulocommutativity
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name of ...
" where a term is in normal form if no rules but commutativity apply.
 The system (pictured) is an example of a weakly normalizing but not strongly normalizing system. ''a'' and ''d'' are normal forms, and ''b'' and ''c'' can be reduced to ''a'' or ''d'', but the infinite reduction ''b'' → ''c'' → ''b'' → ''c'' → ... means that neither ''b'' nor ''c'' is strongly normalizing.
The system (pictured) is an example of a weakly normalizing but not strongly normalizing system. ''a'' and ''d'' are normal forms, and ''b'' and ''c'' can be reduced to ''a'' or ''d'', but the infinite reduction ''b'' → ''c'' → ''b'' → ''c'' → ... means that neither ''b'' nor ''c'' is strongly normalizing.
Untyped lambda calculus
The pure untypedlambda calculus
Lambda calculus (also written as ''λ''-calculus) is a formal system in mathematical logic for expressing computation based on function abstraction and application using variable binding and substitution. It is a universal model of computation ...
does not satisfy the strong normalization property, and not even the weak normalization property. Consider the term (application is left associative). It has the following rewrite rule: For any term ,
:
But consider what happens when we apply to itself:
:
Therefore the term is not strongly normalizing. And this is the only reduction sequence, hence it is not weakly normalizing either.
Typed lambda calculus
Various systems of typed lambda calculus including the simply typed lambda calculus, Jean-Yves Girard's System F, and Thierry Coquand's calculus of constructions are strongly normalizing. A lambda calculus system with the normalization property can be viewed as a programming language with the property that every program terminates. Although this is a very useful property, it has a drawback: a programming language with the normalization property cannot be Turing complete, otherwise one could solve the halting problem by seeing if the program type-checks. That means that there are computable functions that cannot be defined in the simply typed lambda calculus (and similarly there are computable functions that cannot be computed in the calculus of constructions or System F), for example a self-interpreter.See also
* Canonical form * Typed lambda calculus *Rewriting
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a well-formed formula, formula with other terms. Such methods may be achieved by rewriting systems (also known as rewrite systems, rewr ...
* Total functional programming
* Barendregt–Geuvers–Klop conjecture
* Newman's lemma
* Normalization by evaluation
Notes
References
{{DEFAULTSORT:Normal Form (Term Rewriting) Computability theory Formal languages Rewriting systems Lambda calculus Logic in computer science