Euclidean geometry Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry: the ''Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms ...

, the McCay cubic (also called M'Cay cubic or Griffiths cubic) is a

cubic plane curve In mathematics, a cubic plane curve is a plane algebraic curve defined by a cubic equation : applied to homogeneous coordinates for the projective plane; or the inhomogeneous version for the affine space determined by setting in such a ...

in the plane of a reference

triangle A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, any three points, when non- colli ...

and associated with it. It is the third cubic curve in Bernard Gilbert's Catalogue of Triangle Cubics and it is assigned the identification number K003.

Definition

The McCay cubic can be defined by

locus Locus (plural loci) is Latin for "place". It may refer to: Entertainment * Locus (comics), a Marvel Comics mutant villainess, a member of the Mutant Liberation Front * ''Locus'' (magazine), science fiction and fantasy magazine ** ''Locus Award ...

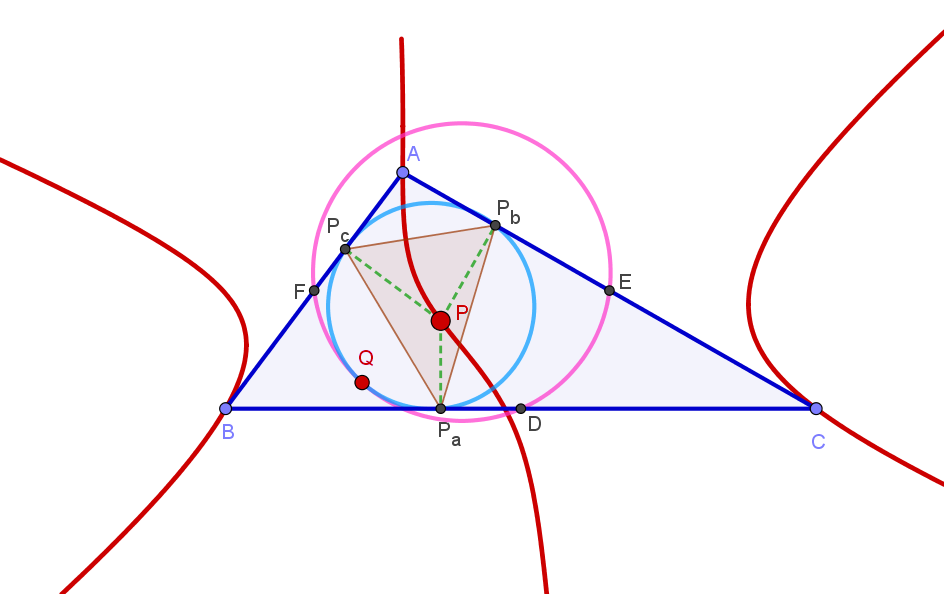
properties in several ways. For example, the McCay cubic is the locus of a point such that the pedal circle of is

tangent In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. Mo ...

to the nine-point circle of the reference triangle . The McCay cubic can also be defined as the locus of point such that the

circumcevian triangle In triangle geometry, a circumcevian triangle is a special triangle associated with the reference triangle and a point in the plane of the triangle. It is also associated with the circumcircle of the reference triangle. Definition Let P be a point ...

of and are orthologic.

Equation of the McCay cubic

The equation of the McCay cubic in barycentric coordinates

x:y:z

is :

\sum_(a^2(b^2+c^2-a^2)x(c^2y^2-b^2z^2))=0.

The equation in

trilinear coordinates In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative directed distances from the three sidelines of the triangle. Trilinear coordinates are an example of homogeneous coordinates. The ratio is ...

\alpha : \beta : \gamma

is :

\alpha (\beta^2 - \gamma^2)\cos A + \beta (\gamma^2 - \alpha^2)\cos B + \gamma (\alpha^2 - \beta^2)\cos C = 0

McCay cubic as a stelloid

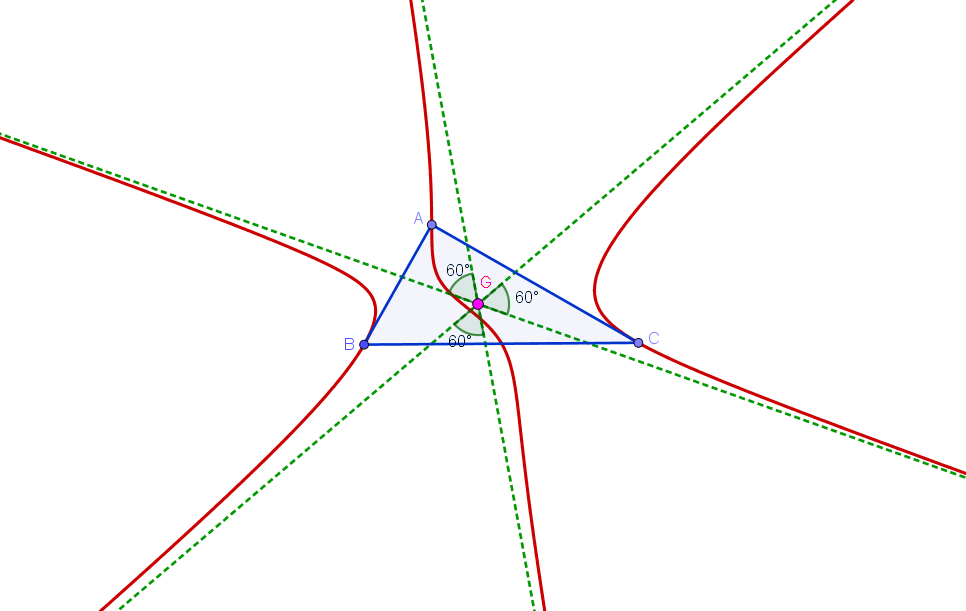
A stelloid is a cubic that has three real concurring

asymptote In analytic geometry, an asymptote () of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the ''x'' or ''y'' coordinates tends to infinity. In projective geometry and related contexts, ...

s making 60° angles with one another. McCay cubic is a stelloid in which the three asymptotes concur at the

centroid In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any ...

of triangle ABC. A circum-stelloid having the same asymptotic directions as those of McCay cubic and concurring at a certain (finite) is called McCay stelloid. The point where the asymptoptes concur is called the "radial center" of the stelloid. Given a finite point X there is one and only one McCay stelloid with X as the radial center.

References

{{reflist Triangle geometry