|
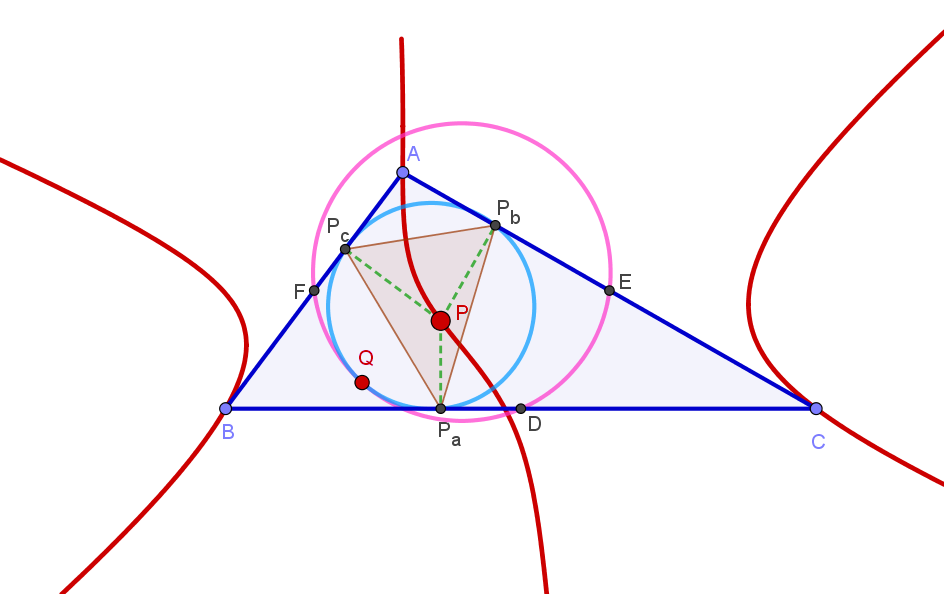
Circumcevian Triangle
In Euclidean geometry, a circumcevian triangle is a special triangle associated with a reference triangle and a point in the plane of the triangle. It is also associated with the circumcircle of the reference triangle. Definition Let be a point in the plane of the reference triangle . Let the lines intersect the circumcircle of at . The triangle is called the circumcevian triangle of with reference to . Coordinates Let be the side lengths of triangle and let the trilinear coordinates of be . Then the trilinear coordinates of the vertices of the circumcevian triangle of are as follows: \begin A' =& -a\beta\gamma &:& (b\gamma+c\beta)\beta &:& (b\gamma+c\beta)\gamma \\ B' =& (c\alpha +a\gamma)\alpha &:& - b\gamma\alpha &:& (c\alpha +a\gamma) \gamma \\ C' =& (a\beta +b\alpha)\alpha &:& (a\beta +b\alpha)\beta &:& - c\alpha\beta \end Some properties *Every triangle inscribed in the circumcircle of the reference triangle ABC is congruent to exactly one circumcevian tria ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. One of those is the parallel postulate which relates to parallel lines on a Euclidean plane. Although many of Euclid's results had been stated earlier,. Euclid was the first to organize these propositions into a logic, logical system in which each result is ''mathematical proof, proved'' from axioms and previously proved theorems. The ''Elements'' begins with plane geometry, still taught in secondary school (high school) as the first axiomatic system and the first examples of mathematical proofs. It goes on to the solid geometry of three dimensions. Much of the ''Elements'' states results of what are now called algebra and number theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimensional line segments. A triangle has three internal angles, each one bounded by a pair of adjacent edges; the sum of angles of a triangle always equals a straight angle (180 degrees or π radians). The triangle is a plane figure and its interior is a planar region. Sometimes an arbitrary edge is chosen to be the ''base'', in which case the opposite vertex is called the ''apex''; the shortest segment between the base and apex is the ''height''. The area of a triangle equals one-half the product of height and base length. In Euclidean geometry, any two points determine a unique line segment situated within a unique straight line, and any three points that do not all lie on the same straight line determine a unique triangle situated w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circumcircle
In geometry, the circumscribed circle or circumcircle of a triangle is a circle that passes through all three vertex (geometry), vertices. The center of this circle is called the circumcenter of the triangle, and its radius is called the circumradius. The circumcenter is the point of intersection (geometry), intersection between the three perpendicular bisectors of the triangle's sides, and is a triangle center. More generally, an -sided polygon with all its vertices on the same circle, also called the circumscribed circle, is called a cyclic polygon, or in the special case , a cyclic quadrilateral. All rectangles, isosceles trapezoids, right kites, and regular polygons are cyclic, but not every polygon is. Straightedge and compass construction The circumcenter of a triangle can be Compass-and-straightedge construction, constructed by drawing any two of the three Bisection#Perpendicular bisectors, perpendicular bisectors. For three non-collinear points, these two lines cannot be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trilinear Coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative directed distances from the three sidelines of the triangle. Trilinear coordinates are an example of homogeneous coordinates. The ratio is the ratio of the perpendicular distances from the point to the sides (extended if necessary) opposite vertices and respectively; the ratio is the ratio of the perpendicular distances from the point to the sidelines opposite vertices and respectively; and likewise for and vertices and . In the diagram at right, the trilinear coordinates of the indicated interior point are the actual distances (, , ), or equivalently in ratio form, for any positive constant . If a point is on a sideline of the reference triangle, its corresponding trilinear coordinate is 0. If an exterior point is on the opposite side of a sideline from the interior of the triangle, its trilinear coordinate associated with that sideline is negative. It is impossible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pedal Triangle
In plane geometry, a pedal triangle is obtained by projecting a point onto the sides of a triangle. More specifically, consider a triangle , and a point that is not one of the vertices . Drop perpendiculars from to the three sides of the triangle (these may need to be produced, i.e., extended). Label the intersections of the lines from with the sides . The pedal triangle is then . If is not an obtuse triangle and is the orthocenter, then the angles of are , and . The quadrilaterals are cyclic quadrilaterals. The location of the chosen point relative to the chosen triangle gives rise to some special cases: * If is the orthocenter, then is the orthic triangle. * If is the incenter, then is the intouch triangle. * If is the circumcenter, then is the medial triangle. *If is on the circumcircle of the triangle, collapses to a line (the ''pedal line'' or ''Simson line''). The vertices of the pedal triangle of an interior point , as shown in the top diag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
McCay Cubic
In Euclidean geometry, the McCay cubic (also called M'Cay cubic or Griffiths cubic) is a cubic plane curve in the plane of a reference triangle and associated with it. It is the third cubic curve in Bernard Gilbert's Catalogue of Triangle Cubics and it is assigned the identification number K003. Definition The McCay cubic can be defined by locus properties in several ways. For example, the McCay cubic is the locus of a point such that the pedal circle of is tangent to the nine-point circle of the reference triangle . The McCay cubic can also be defined as the locus of point such that the circumcevian triangle of and are orthologic. Equation of the McCay cubic The equation of the McCay cubic in barycentric coordinates x:y:z is :\sum_(a^2(b^2+c^2-a^2)x(c^2y^2-b^2z^2))=0. The equation in trilinear coordinates \alpha : \beta : \gamma is :\alpha (\beta^2 - \gamma^2)\cos A + \beta (\gamma^2 - \alpha^2)\cos B + \gamma (\alpha^2 - \beta^2)\cos C = 0 McCay cubic as a stelloid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthologic Triangles
In geometry, two triangles are said to be orthologic if the perpendiculars from the Vertex (geometry), vertices of one of them to the corresponding sides of the other are Concurrent lines, concurrent (i.e., they Line–line intersection, intersect at a single Point (geometry), point). This is a Symmetry (geometry), symmetric property; that is, if the perpendiculars from the vertices of triangle to the sides of triangle are concurrent then the perpendiculars from the vertices of to the sides of are also concurrent. The points of concurrence are known as the orthology centres of the two triangles. Some pairs of orthologic triangles The following are some triangles associated with the reference triangle ABC and orthologic with it. * Medial triangle * Anticomplementary triangle * The triangle whose vertices are the points of contact of the incircle with the sides of ABC * Tangential triangle * The triangle whose vertices are the points of contacts of the excircles with the re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cevian
In geometry, a cevian is a line segment which joins a vertex of a triangle to a point on the opposite side of the triangle. Medians and angle bisectors are special cases of cevians. The name ''cevian'' comes from the Italian mathematician Giovanni Ceva, who proved a theorem about cevians which also bears his name. Length Stewart's theorem The length of a cevian can be determined by Stewart's theorem: in the diagram, the cevian length is given by the formula :\,b^2m + c^2n = a(d^2 + mn). Less commonly, this is also represented (with some rearrangement) by the following mnemonic: :\underset = \!\!\!\!\!\! \underset Median If the cevian happens to be a median (thus bisecting a side), its length can be determined from the formula :\,m(b^2 + c^2) = a(d^2 + m^2) or :\,2(b^2 + c^2) = 4d^2 + a^2 since :\,a = 2m. Hence in this case :d= \frac\sqrt2 . Angle bisector If the cevian happens to be an angle bisector, its length obeys the formulas :\,(b + c)^2 = a^2 \left( \f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ceva's Theorem
In Euclidean geometry, Ceva's theorem is a theorem about triangles. Given a triangle , let the lines be drawn from the vertices to a common point (not on one of the sides of ), to meet opposite sides at respectively. (The segments are known as cevians.) Then, using signed lengths of segments, :\frac \cdot \frac \cdot \frac = 1. In other words, the length is taken to be positive or negative according to whether is to the left or right of in some fixed orientation of the line. For example, is defined as having positive value when is between and and negative otherwise. Ceva's theorem is a theorem of affine geometry, in the sense that it may be stated and proved without using the concepts of angles, areas, and lengths (except for the ratio of the lengths of two line segments that are collinear). It is therefore true for triangles in any affine plane over any field. A slightly adapted converse is also true: If points are chosen on respectively so that : \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |