Mathematics and architecture

Mathematics and architecture are related, since, as with other arts, architects use mathematics for several reasons. Apart from the mathematics needed when engineering buildings, architects use geometry: to define the spatial form of a building; from the Pythagoreans of the sixth century BC onwards, to create forms considered harmonious, and thus to lay out buildings and their surroundings according to mathematical, aesthetic and sometimes religious principles; to decorate buildings with mathematical objects such as tessellations; and to meet environmental goals, such as to minimise wind speeds around the bases of tall buildings.

History

In ancient Egypt, ancient Greece, India, and the Islamic world, buildings including pyramids, temples, mosques, palaces and mausoleums were laid out with specific proportions for religious reasons. In Islamic architecture, geometric shapes and geometric tiling patterns are used to decorate buildings, both inside and outside. Some Hindu temples have a fractal-like structure where parts resemble the whole, conveying a message about the infinite in Hindu cosmology. In Chinese architecture, the tulou of Fujian province are circular, communal defensive structures. In the twenty-first century, mathematical ornamentation is again being used to cover public buildings.

In Renaissance architecture, symmetry and proportion were deliberately emphasized by architects such as Leon Battista Alberti, Sebastiano Serlio and Andrea Palladio, influenced by Vitruvius's ''De architectura'' from ancient Rome and the arithmetic of the Pythagoreans from ancient Greece.
At the end of the nineteenth century, Vladimir Shukhov in Russia and Antoni Gaudí in Barcelona pioneered the use of hyperboloid structures; in the Sagrada Família, Gaudí also incorporated hyperbolic paraboloids, tessellations, catenary arches, catenoids, helicoids, and ruled surfaces. In the twentieth century, styles such as modern architecture and Deconstructivism explored different geometries to achieve desired effects. Minimal surfaces have been exploited in tent-like roof coverings as at Denver International Airport, while Richard Buckminster Fuller pioneered the use of the strong thin-shell structures known as geodesic domes.

Connected fields

The architects Michael Ostwald and Kim Williams, considering the relationships between architecture and mathematics, note that the fields as commonly understood might seem to be only weakly connected, since architecture is a profession concerned with the practical matter of making buildings, while mathematics is the pure study of number and other abstract objects. But, they argue, the two are strongly connected, and have been since antiquity. In ancient Rome, Vitruvius described an architect as a man who knew enough of a range of other disciplines, primarily geometry, to enable him to oversee skilled artisans in all the other necessary areas, such as masons and carpenters. The same applied in the Middle Ages, where graduates learnt arithmetic, geometry and aesthetics alongside the basic syllabus of grammar, logic, and rhetoric (the trivium) in elegant halls made by master builders who had guided many craftsmen. A master builder at the top of his profession was given the title of architect or engineer. In the Renaissance, the quadrivium of arithmetic, geometry, music and astronomy became an extra syllabus expected of the Renaissance man such as Leon Battista Alberti. Similarly in England, Sir Christopher Wren, known today as an architect, was firstly a noted astronomer.

Williams and Ostwald, further overviewing the interaction of mathematics and architecture since 1500 according to the approach of the German sociologist Theodor Adorno, identify three tendencies among architects, namely: to be ''revolutionary'', introducing wholly new ideas; ''reactionary'', failing to introduce change; or '' revivalist'', actually going backwards. They argue that architects have avoided looking to mathematics for inspiration in revivalist times. This would explain why in revivalist periods, such as the Gothic Revival in 19th century England, architecture had little connection to mathematics. Equally, they note that in reactionary times such as the Italian Mannerism of about 1520 to 1580, or the 17th century Baroque and Palladian movements, mathematics was barely consulted. In contrast, the revolutionary early 20th century movements such as Futurism and Constructivism actively rejected old ideas, embracing mathematics and leading to Modernist architecture. Towards the end of the 20th century, too, fractal geometry was quickly seized upon by architects, as was aperiodic tiling, to provide interesting and attractive coverings for buildings.

Architects use mathematics for several reasons, leaving aside the necessary use of mathematics in the engineering of buildings. Firstly, they use geometry because it defines the spatial form of a building. Secondly, they use mathematics to design forms that are considered beautiful or harmonious. From the time of the Pythagoreans with their religious philosophy of number, architects in ancient Greece, ancient Rome, the Islamic world and the Italian Renaissance have chosen the proportions of the built environment – buildings and their designed surroundings – according to mathematical as well as aesthetic and sometimes religious principles. Thirdly, they may use mathematical objects such as tessellations to decorate buildings. Fourthly, they may use mathematics in the form of computer modelling to meet environmental goals, such as to minimise whirling air currents at the base of tall buildings.

Secular aesthetics

Ancient Rome

Vitruvius

The influential ancient Roman architect Vitruvius argued that the design of a building such as a temple depends on two qualities, proportion and ''symmetria''. Proportion ensures that each part of a building relates harmoniously to every other part. ''Symmetria'' in Vitruvius's usage means something closer to the English term modularity than mirror symmetry, as again it relates to the assembling of (modular) parts into the whole building. In his Basilica at Fano, he uses ratios of small integers, especially the triangular numbers (1, 3, 6, 10, ...) to proportion the structure into (Vitruvian) modules. Thus the Basilica's width to length is 1:2; the aisle around it is as high as it is wide, 1:1; the columns are five feet thick and fifty feet high, 1:10.

Vitruvius named three qualities required of architecture in his ''De architectura'', c. 15 B.C.: firmness, usefulness (or "Commodity" in Henry Wotton's 16th century English), and delight. These can be used as categories for classifying the ways in which mathematics is used in architecture. Firmness encompasses the use of mathematics to ensure a building stands up, hence the mathematical tools used in design and to support construction, for instance to ensure stability and to model performance. Usefulness derives in part from the effective application of mathematics, reasoning about and analysing the spatial and other relationships in a design. Delight is an attribute of the resulting building, resulting from the embodying of mathematical relationships in the building; it includes aesthetic, sensual and intellectual qualities.

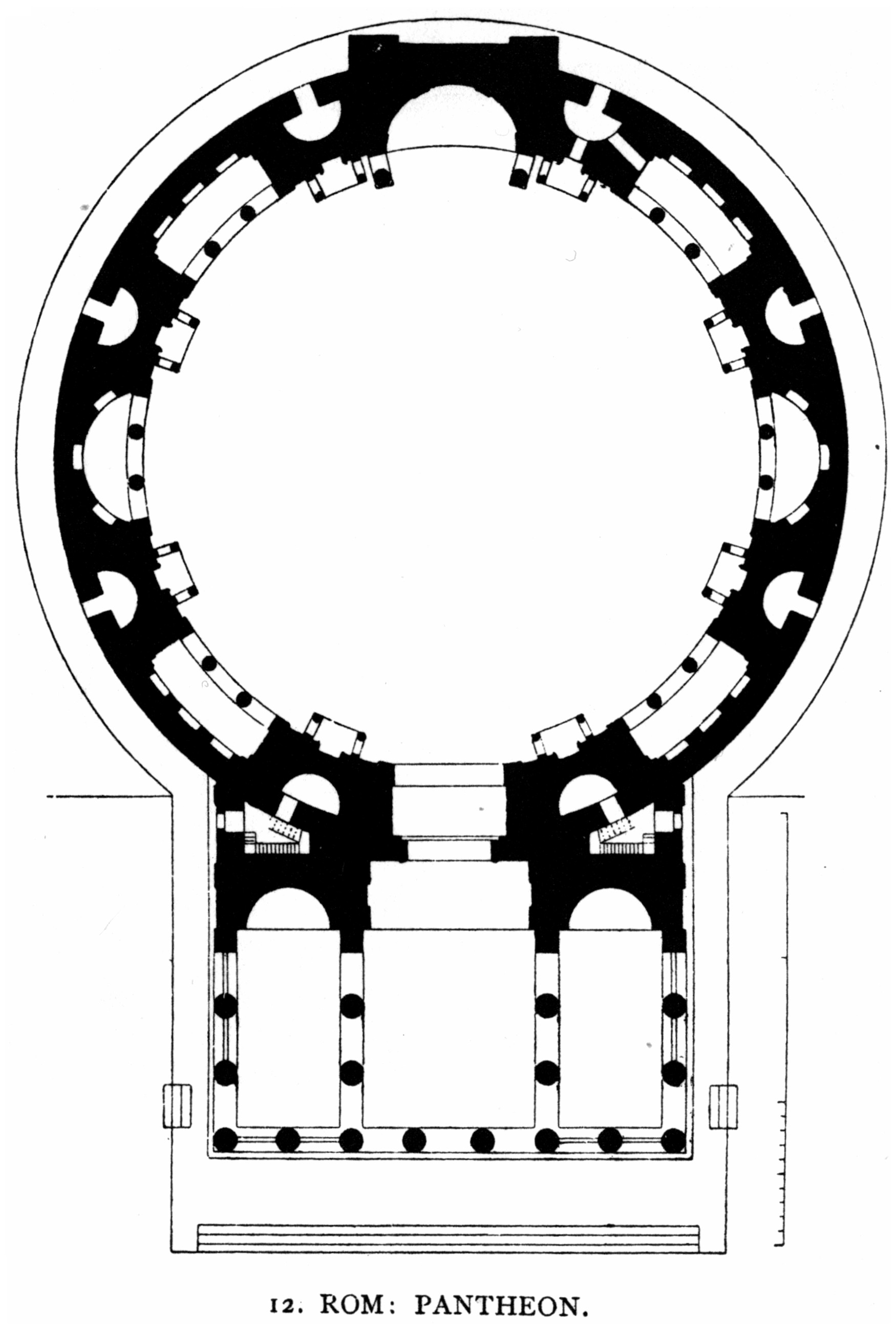
The Pantheon

The Pantheon in Rome has survived intact, illustrating classical Roman structure, proportion, and decoration. The main structure is a dome, the apex left open as a circular oculus to let in light; it is fronted by a short colonnade with a triangular pediment. The height to the oculus and the diameter of the interior circle are the same, , so the whole interior would fit exactly within a cube, and the interior could house a sphere of the same diameter. These dimensions make more sense when expressed in ancient Roman units of measurement: The dome spans 150 Roman feet); the oculus is 30 Roman feet in diameter; the doorway is 40 Roman feet high. The Pantheon remains the world's largest unreinforced concrete dome.

Renaissance

The first Renaissance treatise on architecture was Leon Battista Alberti's 1450 '' De re aedificatoria'' (On the Art of Building); it became the first printed book on architecture in 1485. It was partly based on Vitruvius's ''De architectura'' and, via Nicomachus, Pythagorean arithmetic. Alberti starts with a cube, and derives ratios from it. Thus the diagonal of a face gives the ratio 1:, while the diameter of the sphere which circumscribes the cube gives 1:. Alberti also documented Filippo Brunelleschi's discovery of linear perspective, developed to enable the design of buildings which would look beautifully proportioned when viewed from a convenient distance.

The next major text was Sebastiano Serlio's ''Regole generali d'architettura'' (General Rules of Architecture); the first volume appeared in Venice in 1537; the 1545 volume (books1 and 2) covered geometry and perspective. Two of Serlio's methods for constructing perspectives were wrong, but this did not stop his work being widely used.

In 1570, Andrea Palladio published the influential '' I quattro libri dell'architettura'' (The Four Books of Architecture) in Venice. This widely printed book was largely responsible for spreading the ideas of the Italian Renaissance throughout Europe, assisted by proponents like the English diplomat Henry Wotton with his 1624 ''The Elements of Architecture''. The proportions of each room within the villa were calculated on simple mathematical ratios like 3:4 and 4:5, and the different rooms within the house were interrelated by these ratios. Earlier architects had used these formulas for balancing a single symmetrical facade; however, Palladio's designs related to the whole, usually square, villa. Palladio permitted a range of ratios in the ''Quattro libri'', stating:

In 1615, Vincenzo Scamozzi published the late Renaissance treatise ''L'idea dell'architettura universale'' (The Idea of a Universal Architecture). He attempted to relate the design of cities and buildings to the ideas of Vitruvius and the Pythagoreans, and to the more recent ideas of Palladio.

Nineteenth century

Hyperboloid structures were used starting towards the end of the nineteenth century by Vladimir Shukhov for masts, lighthouses and cooling towers. Their striking shape is both aesthetically interesting and strong, using structural materials economically. Shukhov's first hyperboloidal tower was exhibited in Nizhny Novgorod in 1896.

Twentieth century

The early twentieth century movement Modern architecture, pioneered by Russian Constructivism, used rectilinear Euclidean (also called Cartesian) geometry. In the De Stijl movement, the horizontal and the vertical were seen as constituting the universal. The architectural form consists of putting these two directional tendencies together, using roof planes, wall planes and balconies, which either slide past or intersect each other, as in the 1924 Rietveld Schröder House by Gerrit Rietveld.

Modernist architects were free to make use of curves as well as planes. Charles Holden's 1933 Arnos station has a circular ticket hall in brick with a flat concrete roof. In 1938, the Bauhaus painter László Moholy-Nagy adopted Raoul Heinrich Francé's seven biotechnical elements, namely the crystal, the sphere, the cone, the plane, the (cuboidal) strip, the (cylindrical) rod, and the spiral, as the supposed basic building blocks of architecture inspired by nature.

Le Corbusier proposed an anthropometric scale of proportions in architecture, the Modulor, based on the supposed height of a man. Le Corbusier's 1955 Chapelle Notre-Dame du Haut uses free-form curves not describable in mathematical formulae. The shapes are said to be evocative of natural forms such as the prow of a ship or praying hands. The design is only at the largest scale: there is no hierarchy of detail at smaller scales, and thus no fractal dimension; the same applies to other famous twentieth-century buildings such as the Sydney Opera House, Denver International Airport, and the Guggenheim Museum, Bilbao.

Contemporary architecture, in the opinion of the 90 leading architects who responded to a 2010 World Architecture Survey, is extremely diverse; the best was judged to be Frank Gehry's Guggenheim Museum, Bilbao.

Denver International Airport's terminal building, completed in 1995, has a fabric roof supported as a minimal surface (i.e., its mean curvature is zero) by steel cables. It evokes Colorado's snow-capped mountains and the teepee tents of Native Americans.

The architect Richard Buckminster Fuller is famous for designing strong thin-shell structures known as geodesic domes. The Montréal Biosphère dome is high; its diameter is .

Sydney Opera House has a dramatic roof consisting of soaring white vaults, reminiscent of ship's sails; to make them possible to construct using standardized components, the vaults are all composed of triangular sections of spherical shells with the same radius. These have the required uniform curvature in every direction.

The late twentieth century movement Deconstructivism creates deliberate disorder with what Nikos Salingaros in '' A Theory of Architecture'' calls random forms of high complexity by using non-parallel walls, superimposed grids and complex 2-D surfaces, as in Frank Gehry's Disney Concert Hall and Guggenheim Museum, Bilbao. Until the twentieth century, architecture students were obliged to have a grounding in mathematics. Salingaros argues that first "overly simplistic, politically-driven" Modernism and then "anti-scientific" Deconstructivism have effectively separated architecture from mathematics. He believes that this "reversal of mathematical values" is harmful, as the "pervasive aesthetic" of non-mathematical architecture trains people "to reject mathematical information in the built environment"; he argues that this has negative effects on society. Updated version of

File:Bauhaus-Dessau Wohnheim Balkone.jpg, New Objectivity: Walter Gropius's Bauhaus, Dessau, 1925
File:Arnos Grove underground station 16 November 2012.jpg, cylinder (geometry), Cylinder: Charles Holden's Arnos Grove tube station, 1933
File:RonchampCorbu.jpg, Modern Architecture, Modernism: Le Corbusier's Chapelle Notre Dame du Haut, 1955
File:Mtl. Biosphere in Sept. 2004.jpg, Geodesic dome: the Montréal Biosphère by R. Buckminster Fuller, 1967
File:Sydney Opera House Sails.jpg, Uniform curvature: Sydney Opera House, 1973
File:Image-Disney Concert Hall by Carol Highsmith edit-2.jpg, Deconstructivism: Disney Concert Hall, Los Angeles, 2003

Religious principles

Ancient Egypt

The pyramids of ancient Egypt are Ancient Egyptian funerary practices, tombs constructed with mathematical proportions, but which these were, and whether the Pythagorean theorem was used, are debated. The ratio of the slant height to half the base length of the Great Pyramid of Giza is less than 1% from the golden ratio. If this was the design method, it would imply the use of Kepler triangle, Kepler's triangle (face angle 51°49'), but according to many History of science, historians of science, the golden ratio was not known until the time of the Pythagoreans. The Great Pyramid may also have been based on a triangle with base to hypotenuse ratio 1:4/π (face angle 51°50').

The proportions of some pyramids may have also been based on the Special right triangles, 3:4:5 triangle (face angle 53°8'), known from the Rhind Mathematical Papyrus (c. 1650–1550 BC); this was first conjectured by historian Moritz Cantor in 1882. It is known that right angles were laid out accurately in ancient Egypt using knotted cords for measurement, that Plutarch recorded in ''De Iside et Osiride, Isis and Osiris'' (c. 100 AD) that the Egyptians admired the 3:4:5 triangle, and that a scroll from before 1700 BC demonstrated basic Square (algebra), square formulas. Historian Roger L. Cooke observes that "It is hard to imagine anyone being interested in such conditions without knowing the Pythagorean theorem," but also notes that no Egyptian text before 300 BC actually mentions the use of the theorem to find the length of a triangle's sides, and that there are simpler ways to construct a right angle. Cooke concludes that Cantor's conjecture remains uncertain; he guesses that the ancient Egyptians probably knew the Pythagorean theorem, but "there is no evidence that they used it to construct right angles."

Ancient India

Vaastu Shastra, the ancient Indian canons of architecture and town planning, employs symmetrical drawings called mandalas. Complex calculations are used to arrive at the dimensions of a building and its components. The designs are intended to integrate architecture with nature, the relative functions of various parts of the structure, and ancient beliefs utilizing geometric patterns (yantra), symmetry and Direction (geometry, geography), directional alignments. However, early builders may have come upon mathematical proportions by accident. The mathematician Georges Ifrah notes that simple "tricks" with string and stakes can be used to lay out geometric shapes, such as ellipses and right angles.

The mathematics of fractals has been used to show that the reason why existing buildings have universal appeal and are visually satisfying is because they provide the viewer with a sense of scale at different viewing distances. For example, in the tall gopuram gatehouses of Hindu temples such as the Virupaksha Temple, Hampi, Virupaksha Temple at Hampi built in the seventh century, and others such as the Kandariya Mahadev Temple at Khajuraho, the parts and the whole have the same character, with fractal dimension in the range 1.7 to 1.8. The cluster of smaller towers (''shikhara'', lit. 'mountain') about the tallest, central, tower which represents the holy Mount Kailash, abode of Lord Shiva, depicts the endless repetition of universes in Hindu cosmology. The religious studies scholar William J. Jackson observed of the pattern of towers grouped among smaller towers, themselves grouped among still smaller towers, that:

The Meenakshi Amman Temple is a large complex with multiple shrines, with the streets of Madurai laid out concentrically around it according to the shastras. The four gateways are tall towers (gopurams) with fractal-like repetitive structure as at Hampi. The enclosures around each shrine are rectangular and surrounded by high stone walls.

Ancient Greece

Pythagoras (c. 569 – c. 475 B.C.) and his followers, the Pythagoreans, held that "all things are numbers". They observed the harmonies produced by notes with specific small-integer ratios of frequency, and argued that buildings too should be designed with such ratios. The Greek word ''symmetria'' originally denoted the harmony of architectural shapes in precise ratios from a building's smallest details right up to its entire design.

The Parthenon is long, wide and high to the cornice. This gives a ratio of width to length of 4:9, and the same for height to width. Putting these together gives height:width:length of 16:36:81, or to the delight of the Pythagoreans 4²:6²:9². This sets the module as 0.858 m. A 4:9 rectangle can be constructed as three contiguous rectangles with sides in the ratio 3:4. Each half-rectangle is then a convenient 3:4:5 right triangle, enabling the angles and sides to be checked with a suitably knotted rope. The inner area (naos) similarly has 4:9 proportions ( wide by 48.3 m long); the ratio between the diameter of the outer columns, , and the spacing of their centres, , is also 4:9.

The Parthenon is considered by authors such as John Julius Norwich "the most perfect Doric temple ever built". Its elaborate architectural refinements include "a subtle correspondence between the curvature of the stylobate, the taper of the naos (architecture), naos walls and the ''entasis'' of the columns". ''Entasis'' refers to the subtle diminution in diameter of the columns as they rise. The stylobate is the platform on which the columns stand. As in other classical Greek temples, the platform has a slight parabolic upward curvature to shed rainwater and reinforce the building against earthquakes. The columns might therefore be supposed to lean outwards, but they actually lean slightly inwards so that if they carried on, they would meet about a kilometre and a half above the centre of the building; since they are all the same height, the curvature of the outer stylobate edge is transmitted to the architrave and roof above: "all follow the rule of being built to delicate curves".

The golden ratio was known in 300 B.C., when Euclid described the method of geometric construction. It has been argued that the golden ratio was used in the design of the Parthenon and other ancient Greek buildings, as well as sculptures, paintings, and vases. More recent authors such as Nikos Salingaros, however, doubt all these claims. Experiments by the computer scientist George Markowsky failed to find any preference for the golden rectangle.

Islamic architecture

The historian of Islamic art Antonio Fernandez-Puertas suggests that the Alhambra, like the Great Mosque of Cordoba, was designed using the Al-Andalus, Hispano-Muslim foot or ''codo'' of about . In the palace's Court of the Lions, the proportions follow a series of surd (mathematics), surds. A rectangle with sides 1and has (by Pythagorean theorem, Pythagoras's theorem) a diagonal of , which describes the right triangle made by the sides of the court; the series continues with (giving a 1:2 ratio), and so on. The decorative patterns are similarly proportioned, generating squares inside circles and eight-pointed stars, generating six-pointed stars. There is no evidence to support earlier claims that the golden ratio was used in the Alhambra. The Court of the Lions is bracketed by the Hall of Two Sisters and the Hall of the Abencerrajes; a regular hexagon can be drawn from the centres of these two halls and the four inside corners of the Court of the Lions.

The Selimiye Mosque, Edirne, Selimiye Mosque in Edirne, Turkey, was built by Mimar Sinan to provide a space where the mihrab could be see from anywhere inside the building. The very large central space is accordingly arranged as an octagon, formed by eight enormous pillars, and capped by a circular dome of diameter and high. The octagon is formed into a square with four semidomes, and externally by four exceptionally tall minarets, tall. The building's plan is thus a circle, inside an octagon, inside a square.

Mughal architecture

Mughal architecture, as seen in the abandoned imperial city of Fatehpur Sikri and the Taj Mahal complex, has a distinctive mathematical order and a strong aesthetic based on symmetry and harmony.

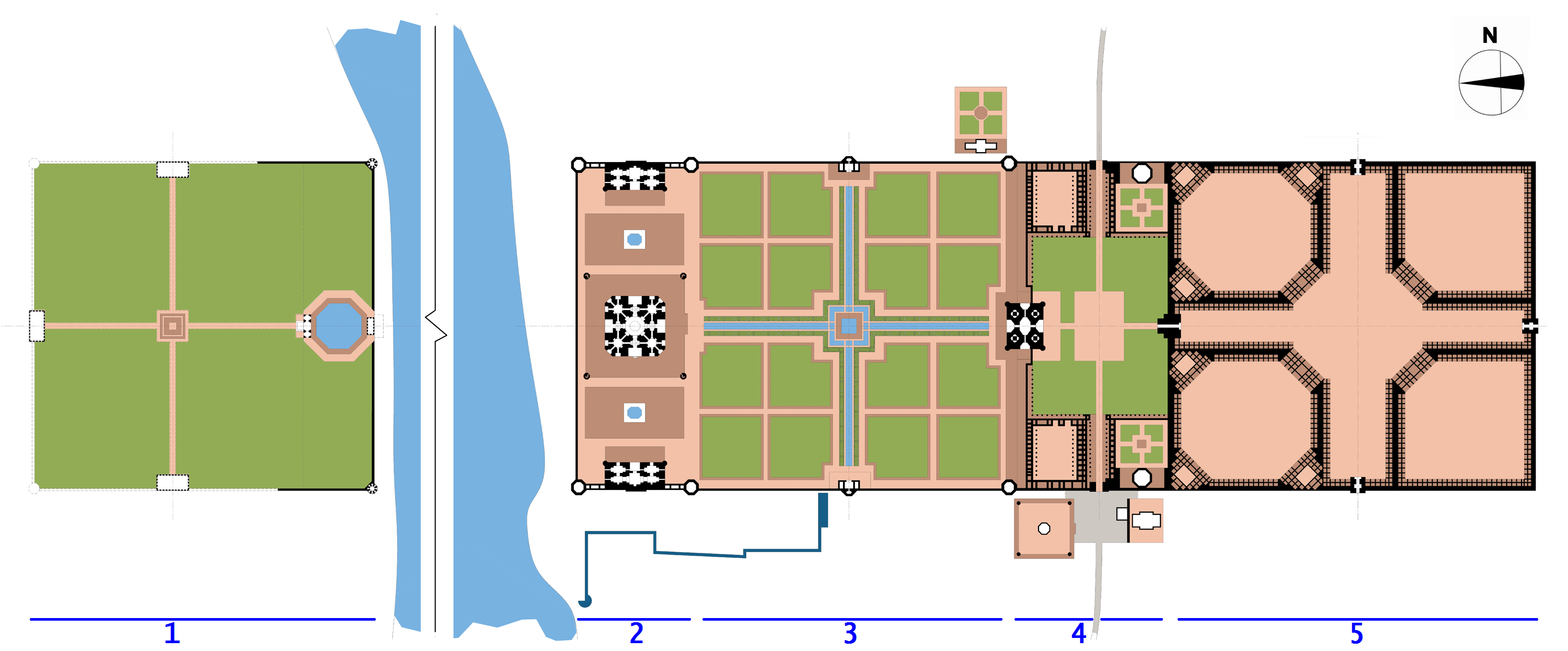
The Taj Mahal exemplifies Mughal architecture, both representing paradise and displaying the list of Mughal emperors, Mughal Emperor Shah Jahan's power through its scale, symmetry and costly decoration. The white marble mausoleum, decorated with pietra dura, the great gate (''Darwaza-i rauza''), other buildings, the gardens and paths together form a unified hierarchical design. The buildings include a mosque in red sandstone on the west, and an almost identical building, the Jawab or 'answer' on the east to maintain the bilateral symmetry of the complex. The formal charbagh ('fourfold garden') is in four parts, symbolising the four rivers of Paradise, and offering views and reflections of the mausoleum. These are divided in turn into 16 parterres.

The Taj Mahal complex was laid out on a grid, subdivided into smaller grids. The historians of architecture Koch and Barraud agree with the traditional accounts that give the width of the complex as 374 Mughal yards or gaz (measure), gaz, the main area being three 374-gaz squares. These were divided in areas like the bazaar and caravanserai into 17-gaz modules; the garden and terraces are in modules of 23 gaz, and are 368 gaz wide (16 x 23). The mausoleum, mosque and guest house are laid out on a grid of 7gaz. Koch and Barraud observe that if an octagon, used repeatedly in the complex, is given sides of 7units, then it has a width of 17 units, which may help to explain the choice of ratios in the complex.

Christian architecture

The Christianity, Christian Ecumenical Patriarch of Constantinople, patriarchal basilica of Haghia Sophia in Byzantium (now Istanbul), first constructed in 537 (and twice rebuilt), was for a thousand years the largest cathedral ever built. It inspired many later buildings including Sultan Ahmed Mosque, Sultan Ahmed and other mosques in the city. The Byzantine architecture includes a nave crowned by a circular dome and two half-domes, all of the same diameter (), with a further five smaller half-domes forming an apse and four rounded corners of a vast rectangular interior. This was interpreted by mediaeval architects as representing the mundane below (the square base) and the divine heavens above (the soaring spherical dome). The emperor Justinian used two geometers, Isidore of Miletus and Anthemius of Tralles as architects; Isidore compiled the works of Archimedes on solid geometry, and was influenced by him.

The importance of water baptism in Christianity was reflected in the scale of baptistry architecture. The oldest, the Lateran Baptistry in Rome, built in 440, set a trend for octagonal baptistries; the baptismal font inside these buildings was often octagonal, though Italy's largest Pisa Baptistry, baptistry, at Pisa, built between 1152 and 1363, is circular, with an octagonal font. It is high, with a diameter of (a ratio of 8:5). Saint Ambrose wrote that fonts and baptistries were octagonal "because on the eighth day, by rising, Christ loosens the bondage of death and receives the dead from their graves."
Saint Augustine similarly described the eighth day as "everlasting ... hallowed by the resurrection of Christ". The octagonal Florence Baptistery, Baptistry of Saint John, Florence, built between 1059 and 1128, is one of the oldest buildings in that city, and one of the last in the direct tradition of classical antiquity; it was extremely influential in the subsequent Florentine Renaissance, as major architects including Francesco Talenti, Alberti and Brunelleschi used it as the model of classical architecture.

The number five is used "exuberantly" in the 1721 Pilgrimage Church of St John of Nepomuk at Zelená hora, near Žďár nad Sázavou in the Czech republic, designed by Jan Santini Aichel, Jan Blažej Santini Aichel. The nave is circular, surrounded by five pairs of columns and five oval domes alternating with ogival apses. The church further has five gates, five chapels, five altars and five stars; a legend claims that when Saint John of Nepomuk was martyred, five stars appeared over his head. The fivefold architecture may also symbolise the five wounds of Christ and the five letters of "Tacui" (Latin: "I kept silence" [about secrets of the confessional]).

Antoni Gaudí used a wide variety of geometric structures, some being minimal surfaces, in the Sagrada Família, Barcelona, started in 1882 (and not completed as of 2015). These include hyperbolic paraboloids and hyperboloid, hyperboloids of revolution, tessellations, catenary arches, catenoids, helicoids, and ruled surfaces. This varied mix of geometries is creatively combined in different ways around the church. For example, in the Passion Façade of Sagrada Família, Gaudí assembled stone "branches" in the form of hyperbolic paraboloids, which overlap at their tops (directrices) without, therefore, meeting at a point. In contrast, in the colonnade there are hyperbolic paraboloidal surfaces that smoothly join other structures to form unbounded surfaces. Further, Gaudí exploits patterns in nature, natural patterns, themselves mathematical, with columns derived from the shapes of trees, and lintels made from unmodified basalt naturally cracked (by cooling from molten rock) into List of places with columnar jointed volcanics, hexagonal columns.

The 1971 Cathedral of Saint Mary of the Assumption (San Francisco, California), Cathedral of Saint Mary of the Assumption, San Francisco has a saddle roof composed of eight segments of hyperbolic paraboloids, arranged so that the bottom horizontal cross section of the roof is a square and the top cross section is a Christian cross. The building is a square on a side, and high. The 1970 Cathedral of Brasília by Oscar Niemeyer makes a different use of a hyperboloid structure; it is constructed from 16 identical concrete beams, each weighing 90 tonnes, arranged in a circle to form a hyperboloid of revolution, the white beams creating a shape like hands praying to heaven. Only the dome is visible from outside: most of the building is below ground.

Several medieval Nordic round churches, churches in Scandinavia are circular, including four on the Danish island of Bornholm. One of the oldest of these, Østerlars Church from c. 1160, has a circular nave around a massive circular stone column, pierced with arches and decorated with a fresco. The circular structure has three storeys and was apparently fortified, the top storey having served for defence.

File:Istanbul 036 (6498284165).jpg, The vaulting of the nave of Haghia Sophia, Istanbul ''(Commons:File:Istanbul 036 (6498284165).jpg, annotations''), 562
File:Battistero Firenze.jpg, The octagonal Florence Baptistery, Baptistry of Saint John, Florence, completed in 1128
File:Jan Santini Aichel - Zelená Hora ground plan 2.jpg, Fivefold symmetries: Jan Santini Aichel's Pilgrimage Church of St John of Nepomuk at Zelená hora, 1721
File:Sagfampassion.jpg, Passion façade of Antoni Gaudí's Sagrada Família, Barcelona, started 1882
File:Catedral1 Rodrigo Marfan.jpg, Oscar Niemeyer's Cathedral of Brasília, 1970
File:St Mary's Cathedral - San Francisco.jpg, The Cathedral of Saint Mary of the Assumption (San Francisco, California), Cathedral of Saint Mary of the Assumption, San Francisco, 1971
File:Oesterlarsfresco.jpg, Central column of Østerlars Church, Østerlars Nordic round church in Bornholm, Denmark

Mathematical decoration

Islamic architectural decoration

Islamic buildings are often decorated with Islamic geometric patterns, geometric patterns which typically make use of several mathematical tessellations, formed of ceramic tiles (girih, zellige) that may themselves be plain or decorated with stripes. Symmetries such as stars with six, eight, or multiples of eight points are used in Islamic patterns. Some of these are based on the 'Khatem Sulemani' or Solomon's seal motif, which is an eight-pointed star made of two squares, one rotated 45 degrees from the other on the same centre. Islamic patterns exploit many of the 17 possible wallpaper groups; as early as 1944, Edith Müller showed that the Alhambra made use of 11 wallpaper groups in its decorations, while in 1986 Branko Grünbaum claimed to have found 13 wallpaper groups in the Alhambra, asserting controversially that the remaining four groups are not found anywhere in Islamic ornament.

File:Sally Port of Sheikh Lotf Allah Mosque.JPG, The complex geometry and tilings of the muqarnas vaulting in the Sheikh Lotfollah Mosque, Isfahan, 1603–1619
File:Louvre Abu Dhabi under construction (cropped).jpg, Louvre Abu Dhabi under construction in 2015, its dome built up of layers of stars made of octagons, triangles, and squares

Modern architectural decoration

Towards the end of the 20th century, novel mathematical constructs such as fractal geometry and aperiodic tiling were seized upon by architects to provide interesting and attractive coverings for buildings. In 1913, the Modernist architect Adolf Loos had declared that "Ornament is a crime", influencing architectural thinking for the rest of the 20th century. In the 21st century, architects are again starting to explore the use of Ornament (art), ornament. 21st century ornamentation is extremely diverse. Henning Larsen's 2011 Harpa Concert and Conference Centre, Reykjavik has what looks like a crystal wall of rock made of large blocks of glass. Foreign Office Architects' 2010 Ravensbourne College, London is tessellated decoratively with 28,000 anodised aluminium tiles in red, white and brown, interlinking circular windows of differing sizes. The tessellation uses three types of tile, an equilateral triangle and two irregular pentagons. Kazumi Kudo's Kanazawa Umimirai Library creates a decorative grid made of small circular blocks of glass set into plain concrete walls.

File:London MMB «T1 Ravensbourne College.jpg, Ravensbourne College, London, 2010
File:Harpa.JPG, Harpa Concert and Conference Centre, Iceland, 2011
File:Umimirai Library.jpg, Kanazawa Umimirai Library, Japan, 2011
File:Museo Soumaya Plaza Carso V.jpg, Museo Soumaya, México, 2011

Defence

Europe

The architecture of fortifications evolved from medieval fortification, medieval fortresses, which had high masonry walls, to low, symmetrical star forts able to resist artillery bombardment between the mid-fifteenth and nineteenth centuries. The geometry of the star shapes was dictated by the need to avoid dead zones where attacking infantry could shelter from defensive fire; the sides of the projecting points were angled to permit such fire to sweep the ground, and to provide crossfire (from both sides) beyond each projecting point. Well-known architects who designed such defences include Michelangelo, Baldassare Peruzzi, Vincenzo Scamozzi and Sébastien Le Prestre de Vauban.

The architectural historian Siegfried Giedion argued that the star-shaped fortification had a formative influence on the patterning of the Renaissance Urban planning, ideal city: "The Renaissance was hypnotized by one city type which for a century and a half—from Filarete to Scamozzi—was impressed upon all utopian schemes: this is the star-shaped city."

File:Coevorden.jpg, Coevorden fortification plan. 17th century
File:Palmanova1600.jpg, Palmanova, Italy, a Republic of Venice, Venetian city within a star fort. 17th century
File:Neuf-Brisach 007 850.jpg, Neuf-Brisach, Alsace, one of the Fortifications of Vauban

China

In Chinese architecture, the tulou of Fujian province are circular, communal defensive structures with mainly blank walls and a single iron-plated wooden door, some dating back to the sixteenth century. The walls are topped with roofs that slope gently both outwards and inwards, forming a ring. The centre of the circle is an open cobbled courtyard, often with a well, surrounded by timbered galleries up to five stories high.

Environmental goals

Architects may also select the form of a building to meet environmental goals. For example, Foster and Partners' 30 St Mary Axe, London, known as "#Top, The Gherkin" for its cucumber-like shape, is a solid of revolution designed using Computer aided design, parametric modelling. Its geometry was chosen not purely for aesthetic reasons, but to minimise whirling air currents at its base. Despite the building's apparently curved surface, all the panels of glass forming its skin are flat, except for the lens at the top. Most of the panels are quadrilaterals, as they can be cut from rectangular glass with less wastage than triangular panels.

The traditional yakhchal (ice pit) of Iran, Persia functioned as an evaporative cooler. Above ground, the structure had a domed shape, but had a subterranean storage space for ice and sometimes food as well. The subterranean space and the thick heat-resistant construction insulated the storage space year round. The internal space was often further cooled with windcatchers.

See also

* Black Rock City
* Mathematics and art
* Patterns in nature

Notes

References

External links

Nexus Network Journal: Architecture and Mathematics Online

The International Society of the Arts, Mathematics, and Architecture



National University of Singapore: Mathematics in Art and Architecture



{{Mathematical art

Mathematics and culture
Architectural theory