Information Fluctuation Complexity

Information fluctuation complexity is an information-theoretic quantity defined as the fluctuation of information about entropy. It is derivable from fluctuations in the predominance of order and chaos in a dynamic system and has been used as a measure of complexity in many diverse fields. It was introduced in a 1993 paper by Bates and Shepard.

Definition

The information fluctuation complexity of a discrete dynamic system is a function of the probability distribution of its states when it is subject to random external input data. The purpose of driving the system with a rich information source such as a random number generator or a white noise signal is to probe the internal dynamics of the system much the same as a frequency-rich impulse is used in signal processing.

If a system has $N$ possible states and the ''state probabilities'' $p_i$are known, then its information entropy is

: $\Eta = \sum_^N p_i I_i = - \sum_^N p_i \log p_i,$

where $I_i = -\log p_i$ is the information content of state $i$.

The information fluctuation complexity of the system is defined as the standard deviation or fluctuation of $I$ about its mean $\Eta$:

: $\sigma_I = \sqrt = \sqrt$

or

: $\sigma_I = \sqrt.$

The ''fluctuation of state information'' $\sigma_I$ is zero in a maximally disordered system with all $p_i = 1/N$; the system simply mimics its random inputs. $\sigma_I$ is also zero when the system is perfectly ordered with just one fixed state $(p_1 = 1)$, regardless of inputs. $\sigma_I$ is non-zero between these two extremes with a mixture of both higher-probability states and lower-probability states populating state space.

Fluctuation of information allows for memory and computation

As a complex dynamic system evolves in time, how it transitions between states depends on external stimuli in an irregular way. At times it may be more sensitive to external stimuli (unstable) and at other times less sensitive (stable). If a particular state has several possible next-states, external information determines which one will be next and the system gains that information by following a particular trajectory in state space. But if several different states all lead to the same next-state, then upon entering the next-state the system loses information about which state preceded it. Thus, a complex system exhibits alternating information gain and loss as it evolves in time. The alternation or fluctuation of information is equivalent to remembering and forgetting — temporary information storage or memory — an essential feature of non-trivial computation.

The gain or loss of information associated with transitions between states can be related to state information. The ''net information gain'' of a transition from state $i$ to state $j$ is the information gained when leaving state $i$ less the information lost when entering state $j$:

: $\Gamma_ = -\log p_ + \log p_.$

Here $p_$ is the ''forward conditional probability'' that if the present state is $i$ then the next state is $j$ and $p_$ is the ''reverse conditional probability'' that if the present state is $j$ then the previous state was $i$. The conditional probabilities are related to the ''transition probability'' $p_$, the probability that a transition from state $i$ to state $j$ occurs, by:

: $p_ = p_i p_ = p_j p_.$

Eliminating the conditional probabilities:

: $\Gamma_ = -\log (p_/p_i) + \log (p_/p_j) = \log p_i - \log p_j = I_j - I_i.$

Therefore the net information gained by the system as a result of the transition depends only on the increase in state information from the initial to the final state. It can be shown that this is true even for multiple consecutive transitions.

$\Gamma = \Delta I$ is reminiscent of the relation between force and potential energy. $I$ is like potential $\Phi$ and $\Gamma$ is like force $\mathbf$ in $\mathbf=$. External information “pushes” a system “uphill” to a state of higher information potential to accomplish memory storage, much like pushing a mass uphill to a state of higher gravitational potential stores energy. The amount of energy storage depends only on the final height, not the path up the hill. Likewise, the amount of information storage does not depend on the transition path between two states in state space. Once a system reaches a rare state with high information potential, it may "fall" to a more common state, losing the previously stored information.

It may be useful to compute the standard deviation of $\Gamma$ about its mean (which is zero), namely the ''fluctuation of net information gain'' $\sigma_\Gamma$, but $\sigma_I$ takes into account multi-transition ''memory loops'' in state space and therefore should be a better indicator of the computational power of a system. Moreover, $\sigma_I$ is easier to calculate because there can be many more transitions than states.

Chaos and order

A dynamic system that is sensitive to external information (unstable) exhibits chaotic behavior whereas one that is insensitive to external information (stable) exhibits orderly behavior. A complex system exhibits both behaviors, fluctuating between them in dynamic balance when subject to a rich information source. The degree of fluctuation is quantified by $\sigma_I$; it captures the alternation in the predominance of chaos and order in a complex system as it evolves in time.

Example: rule 110 variant of the elementary cellular automaton

The rule 110 variant of the elementary cellular automaton has been proven to be capable of universal computation. The proof is based on the existence and interactions of cohesive and self-perpetuating cell patterns known as gliders or spaceships, emergent phenomena, that imply the capability of groups of automaton cells to remember that a glider is passing through them. It is therefore to be expected that there will be memory loops in state space resulting from alternations of information gain and loss, instability and stability, chaos and order.

Consider a 3-cell group of adjacent automaton cells that obey rule 110: . The next state of the center cell depends on the present state of itself and the end cells as specified by the rule:

To calculate the information fluctuation complexity of this system, attach a ''driver cell'' to each end of the 3-cell group to provide a random external stimulus like so, , such that the rule can be applied to the two end cells. Next determine what the next state is for each possible present state and for each possible combination of driver cell contents, to determine the forward conditional probabilities.

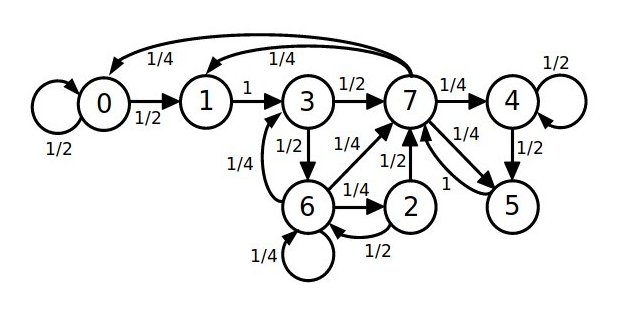
The state diagram of this system is depicted below, with circles representing the states and arrows representing transitions between states. The eight states of this system, to are labeled with the decimal equivalent of the 3-bit contents of the 3-cell group: 7 to 0. The transition arrows are labeled with forward conditional probabilities. Notice that there is variability in the divergence and convergence of arrows corresponding to a variability in chaos and order, sensitivity and insensitivity, gain and loss of external information from the driver cells.

The forward conditional probabilities are determined by the proportion of possible driver cell contents that drive a particular transition. For example, for the four possible combinations of two driver cell contents, state 7 leads to states 5, 4, 1 and 0 so $p_$, $p_$, $p_$, and $p_$ are each 1/4 or 25%. Likewise, state 0 leads to states 0, 1, 0 and 1 so $p_$and $p_$are each 1/2 or 50%. And so forth.

The state probabilities are related by

: $p_j = \sum_^7 p_i p_$ and $\sum_^7 p_i = 1.$

These linear algebraic equations can be solved manually or with the aid of a computer program for the state probabilities, with the following results:

Information entropy and complexity can then be calculated from the state probabilities:

: $\Eta = - \sum_^7 p_i \log_2 p_i = 2.86 \text,$

: $\sigma_I = \sqrt = 0.56 \text.$

Note that the maximum possible entropy for eight states is $\log_2 8 = 3 \text,$ which would be the case if all eight states were equally likely with probabilities of 1/8 (randomness). Thus rule 110 has a relatively high entropy or state utilization at 2.86 bits. But this does not preclude a substantial fluctuation of state information about entropy and thus a substantial value of complexity. Whereas, maximum entropy ''would'' preclude complexity.

An alternative method can be used to obtain the state probabilities when the analytical method used above is unfeasible. Simply drive the system at its inputs (the driver cells) with a random source for many generations and observe the state probabilities empirically. When this is done via computer simulation for 10 million generations the results are as follows:

Since both $\Eta$ and $\sigma_I$ increase with system size, their dimensionless ratio $\sigma_I/\Eta$, the ''relative information fluctuation complexity'', is included to better compare systems of different sizes. Notice that the empirical and analytical results agree for the 3-cell automaton.

In the paper by Bates and Shepard, $\sigma_I$ is computed for all elementary cellular automaton rules and it was observed that the ones that exhibit slow-moving gliders and possibly stationary objects, as rule 110 does, are highly correlated with large values of $\sigma_I$. $\sigma_I$ can therefore be used as a filter to select candidate rules for universal computation, which is tedious to prove.

Applications

Although the derivation of the information fluctuation complexity formula is based on information fluctuations in a dynamic system, the formula depends only on state probabilities and so is also applicable to any probability distribution, including those derived from static images or text.

Over the years the original paper has bee
referred
to by researchers in many diverse fields: complexity theory, complex systems science, chaotic dynamics, environmental engineering, ecological complexity, ecological time-series analysis, ecosystem sustainability, air and water pollution, hydrological wavelet analysis, soil water flow, soil moisture, headwater runoff, groundwater depth, air traffic control, flow patterns and flood events, topology, market forecasting of metal and electricity prices, health informatics, human cognition, human gait kinematics, neurology, EEG analysis, speech analysis, education, investing, and aesthetics.{{Cite thesis, title=Aesthetic Automata: Synthesis and Simulation of Aesthetic Behaviour in Cellular Automata, url=http://research.gold.ac.uk/27681/, publisher=Goldsmiths, University of London, date=2019-11-30, degree=doctoral, doi=10.25602/gold.00027681, first=Mohammad Ali, last=Javaheri Javid

References

Information theory
Entropy and information
Statistical randomness
Complex systems theory
Measures of complexity
Chaos theory
Automata (computation)
Cellular automata