Ibn Al-Haytham

Ḥasan Ibn al-Haytham ( Latinized as Alhazen; ; full name ; ) was a medieval mathematician, astronomer, and physicist of the Islamic Golden Age from present-day Iraq.For the description of his main fields, see e.g. ("He is one of the principal Arab mathematicians and, without any doubt, the best physicist.") , ("Ibn al-Ḥaytam was an eminent eleventh-century Arab optician, geometer, arithmetician, algebraist, astronomer, and engineer."), ("Ibn al-Haytham (d. 1039), known in the West as Alhazan, was a leading Arab mathematician, astronomer, and physicist. His optical compendium, Kitab al-Manazir, is the greatest medieval work on optics.") Referred to as "the father of modern optics", he made significant contributions to the principles of optics and visual perception in particular. His most influential work is titled '' Kitāb al-Manāẓir'' (Arabic: , "Book of Optics"), written during 1011–1021, which survived in a Latin edition. The works of Alhazen were frequently cited during the scientific revolution by Isaac Newton, Johannes Kepler, Christiaan Huygens, and Galileo Galilei.

Ibn al-Haytham was the first to correctly explain the theory of vision, and to argue that vision occurs in the brain, pointing to observations that it is subjective and affected by personal experience. He also stated the principle of least time for refraction which would later become Fermat's principle. He made major contributions to catoptrics and dioptrics by studying reflection, refraction and nature of images formed by light rays. Ibn al-Haytham was an early proponent of the concept that a hypothesis must be supported by experiments based on confirmable procedures or mathematical reasoningan early pioneer in the scientific method five centuries before Renaissance scientists, he is sometimes described as the world's "first true scientist". He was also a polymath, writing on philosophy, theology and medicine.

Born in Basra, he spent most of his productive period in the Fatimid capital of Cairo and earned his living authoring various treatises and tutoring members of the nobilities. Ibn al-Haytham is sometimes given the byname ''al-Baṣrī'' after his birthplace, or ''al-Miṣrī'' ("the Egyptian"). Al-Haytham was dubbed the "Second Ptolemy" by Abu'l-Hasan BayhaqiNoted by Abu'l-Hasan Bayhaqi (c. 1097–1169), and by

Sabra 1994
p. 197

Carl Boyer 1959 p. 80
/ref> and "The Physicist" by John Peckham. Ibn al-Haytham paved the way for the modern science of physical optics.

Biography

Ibn al-Haytham (Alhazen) was born c. 965 to a family of Arab or Persian origin in Basra, Iraq, which was at the time part of the Buyid emirate. His initial influences were in the study of religion and service to the community. At the time, society had a number of conflicting views of religion that he ultimately sought to step aside from religion. This led to him delving into the study of mathematics and science. He held a position with the title of ''vizier'' in his native Basra, and became famous for his knowledge of applied mathematics, as evidenced by his attempt to regulate the flooding of the Nile..

Upon his return to Cairo, he was given an administrative post. After he proved unable to fulfill this task as well, he contracted the ire of the caliph Al-Hakim, and is said to have been forced into hiding until the caliph's death in 1021, after which his confiscated possessions were returned to him.
Legend has it that Alhazen feigned madness and was kept under house arrest during this period. During this time, he wrote his influential '' Book of Optics''. Alhazen continued to live in Cairo, in the neighborhood of the famous University of al-Azhar, and lived from the proceeds of his literary production until his death in c. 1040. (A copy of Apollonius' ''Conics'', written in Ibn al-Haytham's own handwriting exists in Aya Sofya: (MS Aya Sofya 2762, 307 fob., dated Safar 415 A.H. 024.)

Among his students were Sorkhab (Sohrab), a Persian from Semnan, and Abu al-Wafa Mubashir ibn Fatek, an Egyptian prince.

''Book of Optics''

Alhazen's most famous work is his seven-volume treatise on optics ''Kitab al-Manazir'' (''Book of Optics''), written from 1011 to 1021. In it, Ibn al-Haytham was the first to explain that vision occurs when light reflects from an object and then passes to one's eyes, and to argue that vision occurs in the brain, pointing to observations that it is subjective and affected by personal experience.

''Optics'' was translated into Latin by an unknown scholar at the end of the 12th century or the beginning of the 13th century.

This work enjoyed a great reputation during the Middle Ages. The Latin version of ''De aspectibus'' was translated at the end of the 14th century into Italian vernacular, under the title ''De li aspecti''.

It was printed by Friedrich Risner in 1572, with the title ''Opticae thesaurus: Alhazeni Arabis libri septem, nuncprimum editi; Eiusdem liber De Crepusculis et nubium ascensionibus'' (English: Treasury of Optics: seven books by the Arab Alhazen, first edition; by the same, on twilight and the height of clouds).
Risner is also the author of the name variant "Alhazen"; before Risner he was known in the west as Alhacen.
Works by Alhazen on geometric subjects were discovered in the Bibliothèque nationale in Paris in 1834 by E. A. Sedillot. In all, A. Mark Smith has accounted for 18 full or near-complete manuscripts, and five fragments, which are preserved in 14 locations, including one in the Bodleian Library at Oxford, and one in the library of Bruges.

Theory of optics

Two major theories on vision prevailed in classical antiquity. The first theory, the emission theory, was supported by such thinkers as Euclid and Ptolemy, who believed that sight worked by the eye emitting rays of light. The second theory, the intromission theory supported by Aristotle and his followers, had physical forms entering the eye from an object. Previous Islamic writers (such as al-Kindi) had argued essentially on Euclidean, Galenist, or Aristotelian lines. The strongest influence on the ''Book of Optics'' was from Ptolemy's ''Optics'', while the description of the anatomy and physiology of the eye was based on Galen's account. Alhazen's achievement was to come up with a theory that successfully combined parts of the mathematical ray arguments of Euclid, the medical tradition of Galen, and the intromission theories of Aristotle. Alhazen's intromission theory followed al-Kindi (and broke with Aristotle) in asserting that "from each point of every colored body, illuminated by any light, issue light and color along every straight line that can be drawn from that point".. This left him with the problem of explaining how a coherent image was formed from many independent sources of radiation; in particular, every point of an object would send rays to every point on the eye.

What Alhazen needed was for each point on an object to correspond to one point only on the eye. He attempted to resolve this by asserting that the eye would only perceive perpendicular rays from the objectfor any one point on the eye, only the ray that reached it directly, without being refracted by any other part of the eye, would be perceived. He argued, using a physical analogy, that perpendicular rays were stronger than oblique rays: in the same way that a ball thrown directly at a board might break the board, whereas a ball thrown obliquely at the board would glance off, perpendicular rays were stronger than refracted rays, and it was only perpendicular rays which were perceived by the eye. As there was only one perpendicular ray that would enter the eye at any one point, and all these rays would converge on the centre of the eye in a cone, this allowed him to resolve the problem of each point on an object sending many rays to the eye; if only the perpendicular ray mattered, then he had a one-to-one correspondence and the confusion could be resolved. He later asserted (in book seven of the ''Optics'') that other rays would be refracted through the eye and perceived ''as if'' perpendicular. His arguments regarding perpendicular rays do not clearly explain why ''only'' perpendicular rays were perceived; why would the weaker oblique rays not be perceived more weakly? His later argument that refracted rays would be perceived as if perpendicular does not seem persuasive. However, despite its weaknesses, no other theory of the time was so comprehensive, and it was enormously influential, particularly in Western Europe. Directly or indirectly, his ''De Aspectibus'' ( Book of Optics) inspired much activity in optics between the 13th and 17th centuries. Kepler's later theory of the retinal image (which resolved the problem of the correspondence of points on an object and points in the eye) built directly on the conceptual framework of Alhazen.

Alhazen showed through experiment that light travels in straight lines, and carried out various experiments with lenses, mirrors, refraction, and reflection.. His analyses of reflection and refraction considered the vertical and horizontal components of light rays separately.

Alhazen studied the process of sight, the structure of the eye, image formation in the eye, and the visual system. Ian P. Howard argued in a 1996 ''Perception'' article that Alhazen should be credited with many discoveries and theories previously attributed to Western Europeans writing centuries later. For example, he described what became in the 19th century Hering's law of equal innervation. He wrote a description of vertical horopters 600 years before Aguilonius that is actually closer to the modern definition than Aguilonius'sand his work on binocular disparity was repeated by Panum in 1858. Craig Aaen-Stockdale, while agreeing that Alhazen should be credited with many advances, has expressed some caution, especially when considering Alhazen in isolation from Ptolemy, with whom Alhazen was extremely familiar. Alhazen corrected a significant error of Ptolemy regarding binocular vision, but otherwise his account is very similar; Ptolemy also attempted to explain what is now called Hering's law. In general, Alhazen built on and expanded the optics of Ptolemy.

In a more detailed account of Ibn al-Haytham's contribution to the study of binocular vision based on Lejeune and Sabra,. Raynaud showed that the concepts of correspondence, homonymous and crossed diplopia were in place in Ibn al-Haytham's optics. But contrary to Howard, he explained why Ibn al-Haytham did not give the circular figure of the horopter and why, by reasoning experimentally, he was in fact closer to the discovery of Panum's fusional area than that of the Vieth-Müller circle. In this regard, Ibn al-Haytham's theory of binocular vision faced two main limits: the lack of recognition of the role of the retina, and obviously the lack of an experimental investigation of ocular tracts.

Alhazen's most original contribution was that, after describing how he thought the eye was anatomically constructed, he went on to consider how this anatomy would behave functionally as an optical system. His understanding of pinhole projection from his experiments appears to have influenced his consideration of image inversion in the eye, which he sought to avoid. He maintained that the rays that fell perpendicularly on the lens (or glacial humor as he called it) were further refracted outward as they left the glacial humor and the resulting image thus passed upright into the optic nerve at the back of the eye. He followed Galen in believing that the lens was the receptive organ of sight, although some of his work hints that he thought the retina was also involved.

Alhazen's synthesis of light and vision adhered to the Aristotelian scheme, exhaustively describing the process of vision in a logical, complete fashion.

His research in catoptrics (the study of optical systems using mirrors) was centred on spherical and parabolic mirrors and spherical aberration. He made the observation that the ratio between the angle of incidence and refraction does not remain constant, and investigated the magnifying power of a lens.

Law of reflection

Alhazen was the first physicist to give complete statement of the law of reflection. He was first to state that the incident ray, the reflected ray, and the normal to the surface all lie in a same plane perpendicular to reflecting plane.

Alhazen's problem

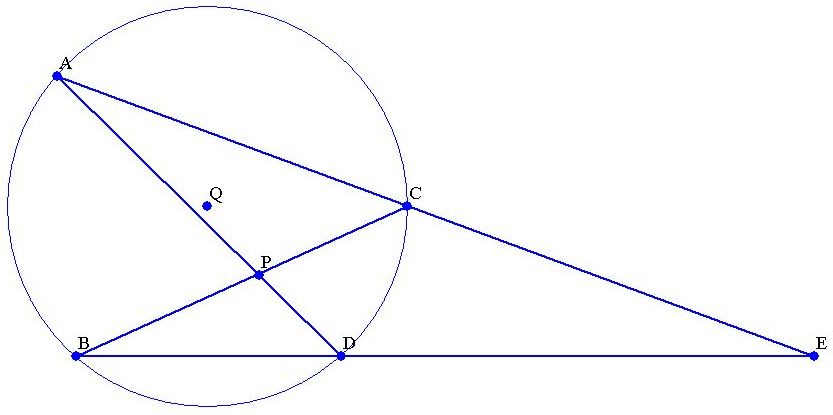His work on catoptrics in Book V of the Book of Optics contains a discussion of what is now known as Alhazen's problem, first formulated by Ptolemy in 150 AD. It comprises drawing lines from two points in the plane of a circle meeting at a point on the circumference and making equal angles with the normal at that point. This is equivalent to finding the point on the edge of a circular billiard table at which a player must aim a cue ball at a given point to make it bounce off the table edge and hit another ball at a second given point. Thus, its main application in optics is to solve the problem, "Given a light source and a spherical mirror, find the point on the mirror where the light will be reflected to the eye of an observer." This leads to an equation of the fourth degree. This eventually led Alhazen to derive a formula for the sum of fourth powers, where previously only the formulas for the sums of squares and cubes had been stated. His method can be readily generalized to find the formula for the sum of any integral powers, although he did not himself do this (perhaps because he only needed the fourth power to calculate the volume of the paraboloid he was interested in). He used his result on sums of integral powers to perform what would now be called an integration, where the formulas for the sums of integral squares and fourth powers allowed him to calculate the volume of a paraboloid. Alhazen eventually solved the problem using conic sections and a geometric proof. His solution was extremely long and complicated and may not have been understood by mathematicians reading him in Latin translation.
Later mathematicians used Descartes' analytical methods to analyse the problem. An algebraic solution to the problem was finally found in 1965 by Jack M. Elkin, an actuarian. Other solutions were discovered in 1989, by Harald Riede and in 1997 by the Oxford mathematician Peter M. Neumann.
Recently, Mitsubishi Electric Research Laboratories (MERL) researchers solved the extension of Alhazen's problem to general rotationally symmetric quadric mirrors including hyperbolic, parabolic and elliptical mirrors.

Camera Obscura

The camera obscura was known to the ancient Chinese, and was described by the Han Chinese polymath Shen Kuo in his scientific book '' Dream Pool Essays'', published in the year 1088 C.E. Aristotle had discussed the basic principle behind it in his ''Problems'', but Alhazen's work contained the first clear description of camera obscura. and early analysis of the device.

Ibn al-Haytham used a camera obscura mainly to observe a partial solar eclipse.
In his essay, Ibn al-Haytham writes that he observed the sickle-like shape of the sun at the time of an eclipse. The introduction reads as follows: "The image of the sun at the time of the eclipse, unless it is total, demonstrates that when its light passes through a narrow, round hole and is cast on a plane opposite to the hole it takes on the form of a moonsickle."

It is admitted that his findings solidified the importance in the history of the camera obscura but this treatise is important in many other respects.

Ancient optics and medieval optics were divided into optics and burning mirrors. Optics proper mainly focused on the study of vision, while burning mirrors focused on the properties of light and luminous rays. ''On the shape of the eclipse'' is probably one of the first attempts made by Ibn al-Haytham to articulate these two sciences.

Very often Ibn al-Haytham's discoveries benefited from the intersection of mathematical and experimental contributions. This is the case with ''On the shape of the eclipse''. Besides the fact that this treatise allowed more people to study partial eclipses of the sun, it especially allowed to better understand how the camera obscura works. This treatise is a physico-mathematical study of image formation inside the camera obscura. Ibn al-Haytham takes an experimental approach, and determines the result by varying the size and the shape of the aperture, the focal length of the camera, the shape and intensity of the light source.

In his work he explains the inversion of the image in the camera obscura, the fact that the image is similar to the source when the hole is small, but also the fact that the image can differ from the source when the hole is large. All these results are produced by using a point analysis of the image.

Refractometer

In the seventh tract of his book of optics, Alhazen described an apparatus for experimenting with various cases of refraction, in order to investigate the relations between the angle of incidence, the angle of refraction and the angle of deflection. This apparatus was a modified version of an apparatus used by Ptolemy for similar purpose.

Unconscious inference

Alhazen basically states the concept of unconscious inference in his discussion of colour before adding that the inferential step between sensing colour and differentiating it is shorter than the time taken between sensing and any other visible characteristic (aside from light), and that "time is so short as not to be clearly apparent to the beholder." Naturally, this suggests that the colour and form are perceived elsewhere. Alhazen goes on to say that information must travel to the central nerve cavity for processing and:

the sentient organ does not sense the forms that reach it from the visible objects until
after it has been affected by these forms; thus it does not sense color as color or light as light until after it has been affected by the form of color or light. Now the affectation received by the sentient organ from the form of color or of light is a certain change; and change must take place in time; .....and it is in the time during which the form extends from the sentient organ's surface to the cavity of the common nerve, and in (the time) following that, that the sensitive faculty, which exists in the whole of the sentient body will perceive color as color...Thus the last sentient's perception of color as such and of light as such takes place at a time following that in which the form arrives from the surface of the sentient organ to the cavity of the common nerve.

Color constancy

Alhazen explained color constancy by observing that the light reflected from an object is modified by the object's color. He explained that the quality of the light and the color of the object are mixed, and the visual system separates light and color. In Book II, Chapter 3 he writes:

Again the light does not travel from the colored object to the eye unaccompanied by the color, nor does the form of the color pass from the colored object to the eye unaccompanied by the light. Neither the form of the light nor that of the color existing in the colored object can pass except as mingled together and the last sentient can only
perceive them as mingled together. Nevertheless, the sentient perceives that the visible object is luminous and that the light seen in the object is other than the color and that these are two properties.

Other contributions

The ''Kitab al-Manazir'' (Book of Optics) describes several experimental observations that Alhazen made and how he used his results to explain certain optical phenomena using mechanical analogies. He conducted experiments with projectiles and concluded that only the impact of perpendicular projectiles on surfaces was forceful enough to make them penetrate, whereas surfaces tended to deflect oblique projectile strikes. For example, to explain refraction from a rare to a dense medium, he used the mechanical analogy of an iron ball thrown at a thin slate covering a wide hole in a metal sheet. A perpendicular throw breaks the slate and passes through, whereas an oblique one with equal force and from an equal distance does not. He also used this result to explain how intense, direct light hurts the eye, using a mechanical analogy: Alhazen associated 'strong' lights with perpendicular rays and 'weak' lights with oblique ones. The obvious answer to the problem of multiple rays and the eye was in the choice of the perpendicular ray, since only one such ray from each point on the surface of the object could penetrate the eye.

Sudanese psychologist Omar Khaleefa has argued that Alhazen should be considered the founder of experimental psychology, for his pioneering work on the psychology of visual perception and optical illusions. Khaleefa has also argued that Alhazen should also be considered the "founder of psychophysics", a sub-discipline and precursor to modern psychology. Although Alhazen made many subjective reports regarding vision, there is no evidence that he used quantitative psychophysical techniques and the claim has been rebuffed.

Alhazen offered an explanation of the Moon illusion, an illusion that played an important role in the scientific tradition of medieval Europe. Many authors repeated explanations that attempted to solve the problem of the Moon appearing larger near the horizon than it does when higher up in the sky. Alhazen argued against Ptolemy's refraction theory, and defined the problem in terms of perceived, rather than real, enlargement. He said that judging the distance of an object depends on there being an uninterrupted sequence of intervening bodies between the object and the observer. When the Moon is high in the sky there are no intervening objects, so the Moon appears close. The perceived size of an object of constant angular size varies with its perceived distance. Therefore, the Moon appears closer and smaller high in the sky, and further and larger on the horizon. Through works by Roger Bacon, John Pecham and Witelo based on Alhazen's explanation, the Moon illusion gradually came to be accepted as a psychological phenomenon, with the refraction theory being rejected in the 17th century. Although Alhazen is often credited with the perceived distance explanation, he was not the first author to offer it. Cleomedes ( 2nd century) gave this account (in addition to refraction), and he credited it to Posidonius ( 135–50 BCE). Ptolemy may also have offered this explanation in his ''Optics'', but the text is obscure. Alhazen's writings were more widely available in the Middle Ages than those of these earlier authors, and that probably explains why Alhazen received the credit.

Scientific method

An aspect associated with Alhazen's optical research is related to systemic and methodological reliance on experimentation (''i'tibar'')(Arabic: اختبار) and controlled testing in his scientific inquiries. Moreover, his experimental directives rested on combining classical physics (''ilm tabi'i'') with mathematics (''ta'alim''; geometry in particular). This mathematical-physical approach to experimental science supported most of his propositions in ''Kitab al-Manazir'' (''The Optics''; ''De aspectibus'' or ''Perspectivae'') and grounded his theories of vision, light and colour, as well as his research in catoptrics and dioptrics (the study of the reflection and refraction of light, respectively)..

According to Matthias Schramm, Alhazen "was the first to make a systematic use of the method of varying the experimental conditions in a constant and uniform manner, in an experiment showing that the intensity of the light-spot formed by the projection of the moonlight through two small apertures onto a screen diminishes constantly as one of the apertures is gradually blocked up." G. J. Toomer expressed some skepticism regarding Schramm's view, partly because at the time (1964) the ''Book of Optics'' had not yet been fully translated from Arabic, and Toomer was concerned that without context, specific passages might be read anachronistically. While acknowledging Alhazen's importance in developing experimental techniques, Toomer argued that Alhazen should not be considered in isolation from other Islamic and ancient thinkers. Toomer concluded his review by saying that it would not be possible to assess Schramm's claim that Ibn al-Haytham was the true founder of modern physics without translating more of Alhazen's work and fully investigating his influence on later medieval writers. G. J. Toomer
Review at Toomer's 1964 review of Matthias Schramm (1963) ''Ibn Al-Haythams Weg Zur Physik''
Toomer p. 464: "Schramm sums up bn Al-Haytham'sachievement in the development of scientific method.", p. 465: "Schramm has demonstrated .. beyond any dispute that Ibn al-Haytham is a major figure in the Islamic scientific tradition, particularly in the creation of experimental techniques." p. 465: "Only when the influence of ibn al-Haytam and others on the mainstream of later medieval physical writings has been seriously investigated can Schramm's claim that ibn al-Haytam was the true founder of modern physics be evaluated."

Other works on physics

Optical treatises

Besides the ''Book of Optics'', Alhazen wrote several other treatises on the same subject, including his ''Risala fi l-Daw (''Treatise on Light''). He investigated the properties of luminance, the rainbow, eclipses, twilight, and moonlight. Experiments with mirrors and the refractive interfaces between air, water, and glass cubes, hemispheres, and quarter-spheres provided the foundation for his theories on catoptrics..

Celestial physics

Alhazen discussed the physics of the celestial region in his ''Epitome of Astronomy'', arguing that Ptolemaic models must be understood in terms of physical objects rather than abstract hypothesesin other words that it should be possible to create physical models where (for example) none of the celestial bodies would collide with each other. The suggestion of mechanical models for the Earth centred Ptolemaic model "greatly contributed to the eventual triumph of the Ptolemaic system among the Christians of the West". Alhazen's determination to root astronomy in the realm of physical objects was important, however, because it meant astronomical hypotheses "were accountable to the laws of physics", and could be criticised and improved upon in those terms.

He also wrote ''Maqala fi daw al-qamar'' (''On the Light of the Moon'').

Mechanics

In his work, Alhazen discussed theories on the motion of a body.

Astronomical works

''On the Configuration of the World''

In his ''On the Configuration of the World'' Alhazen presented a detailed description of the physical structure of the earth:

The book is a non-technical explanation of Ptolemy's '' Almagest'', which was eventually translated into Hebrew and Latin in the 13th and 14th centuries and subsequently had an influence on astronomers such as Georg von Peuerbach. during the European Middle Ages and Renaissance.

''Doubts Concerning Ptolemy''

In his ''Al-Shukūk ‛alā Batlamyūs'', variously translated as ''Doubts Concerning Ptolemy'' or ''Aporias against Ptolemy'', published at some time between 1025 and 1028, Alhazen criticized Ptolemy's ''Almagest'', ''Planetary Hypotheses'', and ''Optics'', pointing out various contradictions he found in these works, particularly in astronomy. Ptolemy's ''Almagest'' concerned mathematical theories regarding the motion of the planets, whereas the ''Hypotheses'' concerned what Ptolemy thought was the actual configuration of the planets. Ptolemy himself acknowledged that his theories and configurations did not always agree with each other, arguing that this was not a problem provided it did not result in noticeable error, but Alhazen was particularly scathing in his criticism of the inherent contradictions in Ptolemy's works.. He considered that some of the mathematical devices Ptolemy introduced into astronomy, especially the equant, failed to satisfy the physical requirement of uniform circular motion, and noted the absurdity of relating actual physical motions to imaginary mathematical points, lines and circles:

Having pointed out the problems, Alhazen appears to have intended to resolve the contradictions he pointed out in Ptolemy in a later work. Alhazen believed there was a "true configuration" of the planets that Ptolemy had failed to grasp. He intended to complete and repair Ptolemy's system, not to replace it completely. In the ''Doubts Concerning Ptolemy'' Alhazen set out his views on the difficulty of attaining scientific knowledge and the need to question existing authorities and theories:

He held that the criticism of existing theorieswhich dominated this bookholds a special place in the growth of scientific knowledge.

''Model of the Motions of Each of the Seven Planets''

Alhazen's ''The Model of the Motions of Each of the Seven Planets'' was written 1038. Only one damaged manuscript has been found, with only the introduction and the first section, on the theory of planetary motion, surviving. (There was also a second section on astronomical calculation, and a third section, on astronomical instruments.) Following on from his ''Doubts on Ptolemy'', Alhazen described a new, geometry-based planetary model, describing the motions of the planets in terms of spherical geometry, infinitesimal geometry and trigonometry. He kept a geocentric universe and assumed that celestial motions are uniformly circular, which required the inclusion of epicycles to explain observed motion, but he managed to eliminate Ptolemy's equant. In general, his model didn't try to provide a causal explanation of the motions, but concentrated on providing a complete, geometric description that could explain observed motions without the contradictions inherent in Ptolemy's model.

Other astronomical works

Alhazen wrote a total of twenty-five astronomical works, some concerning technical issues such as ''Exact Determination of the Meridian'', a second group concerning accurate astronomical observation, a third group concerning various astronomical problems and questions such as the location of the Milky Way; Alhazen made the first systematic effort of evaluating the Milky Way's parallax, combining Ptolemy's data and his own. He concluded that the parallax is (probably very much) smaller than Lunar parallax, and the Milky way should be a celestial object. Though he was not the first who argued that the Milky Way does not belong to the atmosphere, he is the first who did quantitative analysis for the claim.
The fourth group consists of ten works on astronomical theory, including the ''Doubts'' and ''Model of the Motions'' discussed above.

Mathematical works

In mathematics, Alhazen built on the mathematical works of Euclid and Thabit ibn Qurra and worked on "the beginnings of the link between algebra and geometry". Alhazen made developments in conic sections and number theory.

He developed a formula for summing the first 100 natural numbers, using a geometric proof to prove the formula.

Geometry

Alhazen explored what is now known as the Euclidean parallel postulate, the fifth postulate in Euclid's ''Elements'', using a proof by contradiction, and in effect introducing the concept of motion into geometry. He formulated the Lambert quadrilateral, which Boris Abramovich Rozenfeld names the "Ibn al-Haytham–Lambert quadrilateral". He was criticised by Omar Khayyam who pointed that Aristotle had condemned the use of motion in geometry.

In elementary geometry, Alhazen attempted to solve the problem of squaring the circle using the area of lunes (crescent shapes), but later gave up on the impossible task.. The two lunes formed from a right triangle by erecting a semicircle on each of the triangle's sides, inward for the hypotenuse and outward for the other two sides, are known as the lunes of Alhazen; they have the same total area as the triangle itself.

Number theory

Alhazen's contributions to number theory include his work on perfect numbers. In his ''Analysis and Synthesis'', he may have been the first to state that every even perfect number is of the form 2^''n''−1(2^''n'' − 1) where 2^''n'' − 1 is prime, but he was not able to prove this result; Euler later proved it in the 18th century, and it is now called the Euclid–Euler theorem.

Alhazen solved problems involving congruences using what is now called Wilson's theorem. In his ''Opuscula'', Alhazen considers the solution of a system of congruences, and gives two general methods of solution. His first method, the canonical method, involved Wilson's theorem, while his second method involved a version of the Chinese remainder theorem.

Calculus

Alhazen discovered the sum formula for the fourth power, using a method that could be generally used to determine the sum for any integral power. He used this to find the volume of a paraboloid. He could find the integral formula for any polynomial without having developed a general formula.

Other works

''Influence of Melodies on the Souls of Animals''

Alhazen also wrote a ''Treatise on the Influence of Melodies on the Souls of Animals'', although no copies have survived. It appears to have been concerned with the question of whether animals could react to music, for example whether a camel would increase or decrease its pace.

Engineering

In engineering, one account of his career as a civil engineer has him summoned to Egypt by the Fatimid Caliph, Al-Hakim bi-Amr Allah, to regulate the flooding of the Nile River. He carried out a detailed scientific study of the annual inundation of the Nile River, and he drew plans for building a dam, at the site of the modern-day Aswan Dam. His field work, however, later made him aware of the impracticality of this scheme, and he soon feigned madness so he could avoid punishment from the Caliph.

Philosophy

In his ''Treatise on Place'', Alhazen disagreed with Aristotle's view that nature abhors a void, and he used geometry in an attempt to demonstrate that place (''al-makan'') is the imagined three-dimensional void between the inner surfaces of a containing body.. Abd-el-latif, a supporter of Aristotle's philosophical view of place, later criticized the work in ''Fi al-Radd 'ala Ibn al-Haytham fi al-makan'' (''A refutation of Ibn al-Haytham's place'') for its geometrization of place.

Alhazen also discussed space perception and its epistemological implications in his '' Book of Optics''. In "tying the visual perception of space to prior bodily experience, Alhazen unequivocally rejected the intuitiveness of spatial perception and, therefore, the autonomy of vision. Without tangible notions of distance and size for
correlation, sight can tell us next to nothing about such things."

Theology

Alhazen was a Muslim and most sources report that he was a Sunni and a follower of the Ash'ari school.Ishaq, Usep Mohamad, and Wan Mohd Nor Wan Daud. "Tinjauan biografi-bibliografi Ibn al-haytham." Historia : Jurnal Program Studi Pendidikan Sejarah 5.2 (2017): 107–124.Kaminski, Joseph J. "The Trajectory of the Development of Islamic ThoughtA Comparison Between Two Earlier and Two Later Scholars." ''The Contemporary Islamic Governed State.'' Palgrave Macmillan, Cham, 2017. 31–70. "For example, Ibn al-Haytham and Abū Rayhān al-Bīrūnī were among the most important medieval scholars who used the scientific method in their approach to natural science, and they were both Ash'arites" Ziauddin Sardar says that some of the greatest Muslim scientists, such as Ibn al-Haytham and Abū Rayhān al-Bīrūnī, who were pioneers of the scientific method, were themselves followers of the Ashʿari school of Islamic theology. Like other Ashʿarites who believed that faith or ''taqlid'' should apply only to Islam and not to any ancient Hellenistic authorities, Ibn al-Haytham's view that ''taqlid'' should apply only to prophets of Islam and not to any other authorities formed the basis for much of his scientific skepticism and criticism against Ptolemy and other ancient authorities in his ''Doubts Concerning Ptolemy'' and '' Book of Optics''.

Alhazen wrote a work on Islamic theology in which he discussed prophethood and developed a system of philosophical criteria to discern its false claimants in his time.
He also wrote a treatise entitled ''Finding the Direction of Qibla by Calculation'' in which he discussed finding the Qibla, where prayers (salat) are directed towards, mathematically.

There are occasional references to theology or religious sentiment in his technical works, e.g.
in ''Doubts Concerning Ptolemy'':

In ''The Winding Motion'':

Regarding the relation of objective truth and God:

Legacy

Alhazen made significant contributions to optics, number theory, geometry, astronomy and natural philosophy. Alhazen's work on optics is credited with contributing a new emphasis on experiment.

His main work, '' Kitab al-Manazir'' (''Book of Optics''), was known in the Muslim world mainly, but not exclusively, through the thirteenth-century commentary by Kamāl al-Dīn al-Fārisī, the ''Tanqīḥ ''al-Manāẓir'' li-dhawī l-abṣār wa l-baṣā'ir''. In al-Andalus, it was used by the eleventh-century prince of the Banu Hud dynasty of Zaragossa and author of an important mathematical text, al-Mu'taman ibn Hūd. A Latin translation of the ''Kitab al-Manazir'' was made probably in the late twelfth or early thirteenth century. This translation was read by and greatly influenced a number of scholars in Christian Europe including: Roger Bacon, Robert Grosseteste, Witelo, Giambattista della Porta, Leonardo da Vinci, Galileo Galilei, Christiaan Huygens, René Descartes, and Johannes Kepler. Meanwhile, in the Islamic world, Alhazen's work influenced Averroes' writings on optics, and his legacy was further advanced through the 'reforming' of his ''Optics'' by Persian scientist Kamal al-Din al-Farisi (died c. 1320) in the latter's ''Kitab Tanqih al-Manazir'' (''The Revision of'' bn al-Haytham's''Optics''). Alhazen wrote as many as 200 books, although only 55 have survived. Some of his treatises on optics survived only through Latin translation. During the Middle Ages his books on cosmology were translated into Latin, Hebrew and other languages.

H. J. J. Winter, a British historian of science, summing up the importance of Ibn al-Haytham in the history of physics wrote:

After the death of Archimedes no really great physicist appeared until Ibn al-Haytham. If, therefore, we confine our interest only to the history of physics, there is a long period of over twelve hundred years during which the Golden Age of Greece gave way to the era of Muslim Scholasticism, and the experimental spirit of the noblest physicist of Antiquity lived again in the Arab Scholar from Basra.

Although only one commentary on Alhazen's optics has survived the Islamic Middle Ages, Geoffrey Chaucer mentions the work in ''The Canterbury Tales'':

"They spoke of Alhazen and Vitello,
And Aristotle, who wrote, in their lives,
On strange mirrors and optical instruments."

The impact crater Alhazen on the Moon is named in his honour, as was the asteroid 59239 Alhazen. In honour of Alhazen, the Aga Khan University (Pakistan) named its Ophthalmology endowed chair as "The Ibn-e-Haitham Associate Professor and Chief of Ophthalmology".

The 2015 International Year of Light celebrated the 1000th anniversary of the works on optics by Ibn Al-Haytham.

In 2014, the " Hiding in the Light" episode of '' Cosmos: A Spacetime Odyssey'', presented by Neil deGrasse Tyson, focused on the accomplishments of Ibn al-Haytham. He was voiced by Alfred Molina in the episode.

Over forty years previously, Jacob Bronowski presented Alhazen's work in a similar television documentary (and the corresponding book), ''The Ascent of Man''. In episode 5 (''The Music of the Spheres''), Bronowski remarked that in his view, Alhazen was "the one really original scientific mind that Arab culture produced", whose theory of optics was not improved on till the time of Newton and Leibniz.

UNESCO declared 2015 the International Year of Light and its Director-General Irina Bokova dubbed Ibn al-Haytham 'the father of optics'. Amongst others, this was to celebrate Ibn Al-Haytham's achievements in optics, mathematics and astronomy. An international campaign, created by the 1001 Inventions organisation, titled ''1001 Inventions and the World of Ibn Al-Haytham'' featuring a series of interactive exhibits, workshops and live shows about his work, partnering with science centers, science festivals, museums, and educational institutions, as well as digital and social media platforms. The campaign also produced and released the short educational film 1001 Inventions and the World of Ibn Al-Haytham.

Ibn al-Haytham appears on the 10,000 dinar banknote of the Iraqi dinar, series 2003.

List of works

According to medieval biographers, Alhazen wrote more than 200 works on a wide range of subjects, of which at least 96 of his scientific works are known. Most of his works are now lost, but more than 50 of them have survived to some extent. Nearly half of his surviving works are on mathematics, 23 of them are on astronomy, and 14 of them are on optics, with a few on other subjects. Not all his surviving works have yet been studied, but some of the ones that have are given below.

# '' Book of Optics'' (كتاب المناظر)
# ''Analysis and Synthesis'' (مقالة في التحليل والتركيب)
# ''Balance of Wisdom'' (ميزان الحكمة)
# ''Corrections to the Almagest'' (تصويبات على المجسطي)
# ''Discourse on Place'' (مقالة في المكان)
# ''Exact Determination of the Pole'' (التحديد الدقيق للقطب)
# ''Exact Determination of the Meridian'' (رسالة في الشفق)
# ''Finding the Direction of Qibla by Calculation'' (كيفية حساب اتجاه القبلة)
# ''Horizontal Sundials'' (المزولة الأفقية)
# ''Hour Lines'' (خطوط الساعة)
# ''Doubts Concerning Ptolemy'' (شكوك على بطليموس)
# ''Maqala fi'l-Qarastun'' (مقالة في قرسطون)
# ''On Completion of the Conics'' (إكمال المخاريط)
# ''On Seeing the Stars'' (رؤية الكواكب)
# ''On Squaring the Circle'' (مقالة فی تربیع الدائرة)
# ''On the Burning Sphere'' (المرايا المحرقة بالدوائر)
# ''On the Configuration of the World'' (تكوين العالم)
# ''On the Form of Eclipse'' (مقالة فی صورة ‌الکسوف)
# ''On the Light of Stars'' (مقالة في ضوء النجوم)Ibn Al-Haytham, W. 'Arafat and H. J. J. Winter (1971) (c. 1027–1038) The Light of the Stars: A Short Discourse by Ibn Al-Haytham ''The British Journal for the History of Science'' Vol. 5, No. 3 (Jun., 1971), pp. 282–288
# ''On the Light of the Moon'' (مقالة في ضوء القمر)
# ''On the Milky Way'' (مقالة في درب التبانة)
# ''On the Nature of Shadows'' (كيفيات الإظلال)
# ''On the Rainbow and Halo'' (مقالة في قوس قزح)
# ''Opuscula'' (Minor Works)
# ''Resolution of Doubts Concerning the Almagest'' (تحليل شكوك حول الجست)
# ''Resolution of Doubts Concerning the Winding Motion''
# ''The Correction of the Operations in Astronomy'' (تصحيح العمليات في الفلك)
# ''The Different Heights of the Planets'' (اختلاف ارتفاع الكواكب)
# ''The Direction of Mecca'' (اتجاه القبلة)
# ''The Model of the Motions of Each of the Seven Planets'' (نماذج حركات الكواكب السبعة)
# ''The Model of the Universe'' (نموذج الكون)
# ''The Motion of the Moon'' (حركة القمر)
# ''The Ratios of Hourly Arcs to their Heights''
# ''The Winding Motion'' (الحركة المتعرجة)
# ''Treatise on Light'' (رسالة في الضوء)Alhacen (c.1035) ''Treatise on Light'' (رسالة في الضوء) as cited in Shmuel Sambursky, ed. (1975
Physical thought from the Presocratics to the quantum physicists : an anthology
p.137
# ''Treatise on Place'' (رسالة في المكان)
# ''Treatise on the Influence of Melodies on the Souls of Animals'' (تأثير اللحون الموسيقية في النفوس الحيوانية)
# كتاب في تحليل المسائل الهندسية (A book in engineering analysis)
# الجامع في أصول الحساب (The whole in the assets of the account)
# قول فی مساحة الکرة (Say in the sphere)
# القول المعروف بالغریب فی حساب المعاملات (Saying the unknown in the calculation of transactions)
# خواص المثلث من جهة العمود (Triangle properties from the side of the column)
# رسالة فی مساحة المسجم المکافی (A message in the free space)
# شرح أصول إقليدس (Explain the origins of Euclid)
# المرايا المحرقة بالقطوع (The burning mirrors of the rainbow)
# مقالة في القرصتن (Treatise on Centers of Gravity)

Lost works

# ''A Book in which I have Summarized the Science of Optics from the Two Books of Euclid and Ptolemy, to which I have added the Notions of the First Discourse which is Missing from Ptolemy's Book''From Ibn Abi Usaibia's catalog, as cited in 91(vol. 1), p. xv.
# ''Treatise on Burning Mirrors''
# ''Treatise on the Nature of he Organ ofSight and on How Vision is Achieved Through It''

See also

* Ibn Sufi
* " Hiding in the Light"
* History of mathematics
* Theoretical physics
* History of optics
* History of physics
* History of science
* History of scientific method
* Hockney–Falco thesis
* Mathematics in medieval Islam
* Physics in medieval Islam
* Science in the medieval Islamic world
* Fatima al-Fihri
* Islamic Golden Age

Notes

References

Sources

*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
* Reprinted in
*
*
*
*
*
*
*
*
*
*
*
*
Books I-III (2001) Vol 1 Commentary and Latin text

Vol 2 English translation I: TOC pp. 339–41, II: TOC pp. 415–16, III: TOC pp. 559–60, Notes 681ff, Bibl.
)
*
*
*
Books 4–5 (2006) 95 4 – Vol 1 Commentary and Latin text

95 5 – Vol 2 English translation IV: TOC pp. 289–94, V: TOC pp. 377–84, Notes, Bibl.
)
*
Book 6 (2008) 98 (#1, section 1) – Vol 1 Commentary and Latin text

98 (#1, section 2) – Vol 2 English translation VI:TOC pp. 155–160, Notes, Bibl.
)
*
Book 7 (2010) 100(#3, section 1) – Vol 1 Commentary and Latin text

100(#3, section 2) – Vol 2 English translation VII: TOC pp. 213–18, Notes, Bibl.
)
*
*
*
*
*
*
*
*
*
*
*

Further reading

Primary

*
*
* 2 vols: . (Philadelphia: American Philosophical Society), 2006 �
95(#2) Books 4–5 Vol 1 Commentary and Latin text

95(#3) Vol 2 English translation, Notes, Bibl.

* Smith, A. Mark, ed. and trans. (2008) ''Alhacen on Image-formation and distortion in mirrors'' : a critical edition, with English translation and commentary, of Book 6 of Alhacen's ''De aspectibus'', he Medieval Latin version of Ibn al-Haytham's ''Kitāb al-Manāzir'' ''Transactions of the American Philosophical Society'', 2 vols: Vol 1 98(#1, section 1 – Vol 1 Commentary and Latin text); 98(#1, section 2 – Vol 2 English translation). (Philadelphia: American Philosophical Society), 2008
Book 6 (2008) Vol 1 Commentary and Latin text

Vol 2 English translation, Notes, Bibl.

* Smith, A. Mark, ed. and trans. (2010) ''Alhacen on Refraction'' : a critical edition, with English translation and commentary, of Book 7 of Alhacen's ''De aspectibus'', he Medieval Latin version of Ibn al-Haytham's ''Kitāb al-Manāzir'' ''Transactions of the American Philosophical Society'', 2 vols: 100(#3, section 1 – Vol 1, Introduction and Latin text); 100(#3, section 2 – Vol 2 English translation). (Philadelphia: American Philosophical Society), 2010.
Book 7 (2010) Vol 1 Commentary and Latin textVol 2 English translation, Notes, Bibl.

Secondary

* Belting, Hans
''Afterthoughts on Alhazen's Visual Theory and Its Presence in the Pictorial Theory of Western Perspective''
in: Variantology 4. On Deep Time Relations of Arts, Sciences and Technologies in the Arabic-Islamic World and Beyond, ed. by Siegfried Zielinski and Eckhard Fürlus in cooperation with Daniel Irrgang and Franziska Latell (Cologne: Verlag der Buchhandlung Walther König, 2010), pp. 19–42.
*
*
*
*
* Graham, Mark. ''How Islam Created the Modern World''. Amana Publications, 2006.
*
* Roshdi Rashed, Optics and Mathematics: Research on the history of scientific thought in Arabic, Variorum reprints, Aldershot, 1992.
* Roshdi Rashed, Geometry and Dioptrics the tenth century: Ibn Sahl al-Quhi and Ibn al-Haytham (in French), Les Belles Lettres, Paris, 1993
* Roshdi Rashed, Infinitesimal Mathematics, vols. 1–5, al-Furqan Islamic Heritage Foundation, London, 1993–2006
*
* Siegfried Zielinski & Franziska Latell, ''How One Sees'', in: Variantology 4. On Deep Time Relations of Arts, Sciences and Technologies in the Arabic-Islamic World and Beyond, ed. by Siegfried Zielinski and Eckhard Fürlus in cooperation with Daniel Irrgang and Franziska Latell (Cologne: Verlag der Buchhandlung Walther König, 2010), pp. 19–42
Buchhandlung Walther-König - KWB 45: Variantology 4

External links

*
*
PDF version


'A Brief Introduction on Ibn al-Haytham' based on a lecture delivered at the Royal Society in London by Nader El-Bizri




The Miracle of Light – a UNESCO article on Ibn al-Haytham




*
*
* ttps://web.archive.org/web/20080708215144/http://www.trincoll.edu/depts/phil/philo/phils/muslim/alhazen.html Biography from Trinity College (Connecticut)
Biography from Molecular Expressions

The First True Scientist
from BBC News

Over the Moon
From The UNESCO Courier on the occasion of the International Year of Astronomy 2009

The Mechanical Water Clock Of Ibn Al-Haytham
Muslim Heritage
* Alhazen's (1572
''Opticae thesaurus''
(English) – digital facsimile from the Linda Hall Library

{{Authority control

960s births
1040 deaths
10th-century mathematicians
11th-century astronomers
11th-century mathematicians
Scholars under the Buyid dynasty
Mathematicians from the Fatimid Caliphate
Iraqi astronomers
Mathematicians under the Buyid dynasty
Engineers of the medieval Islamic world
Medieval physicists
Medieval Islamic philosophers
Philosophers of science
Natural philosophers
People from Basra
Precursors of photography
Scientists who worked on qibla determination
Inventors of the medieval Islamic world
History of scientific method
History of optics
11th-century inventors
Muslim critics of atheism