Hopf Bifurcation on:
[Wikipedia]
[Google]
[Amazon]
 In the
In the
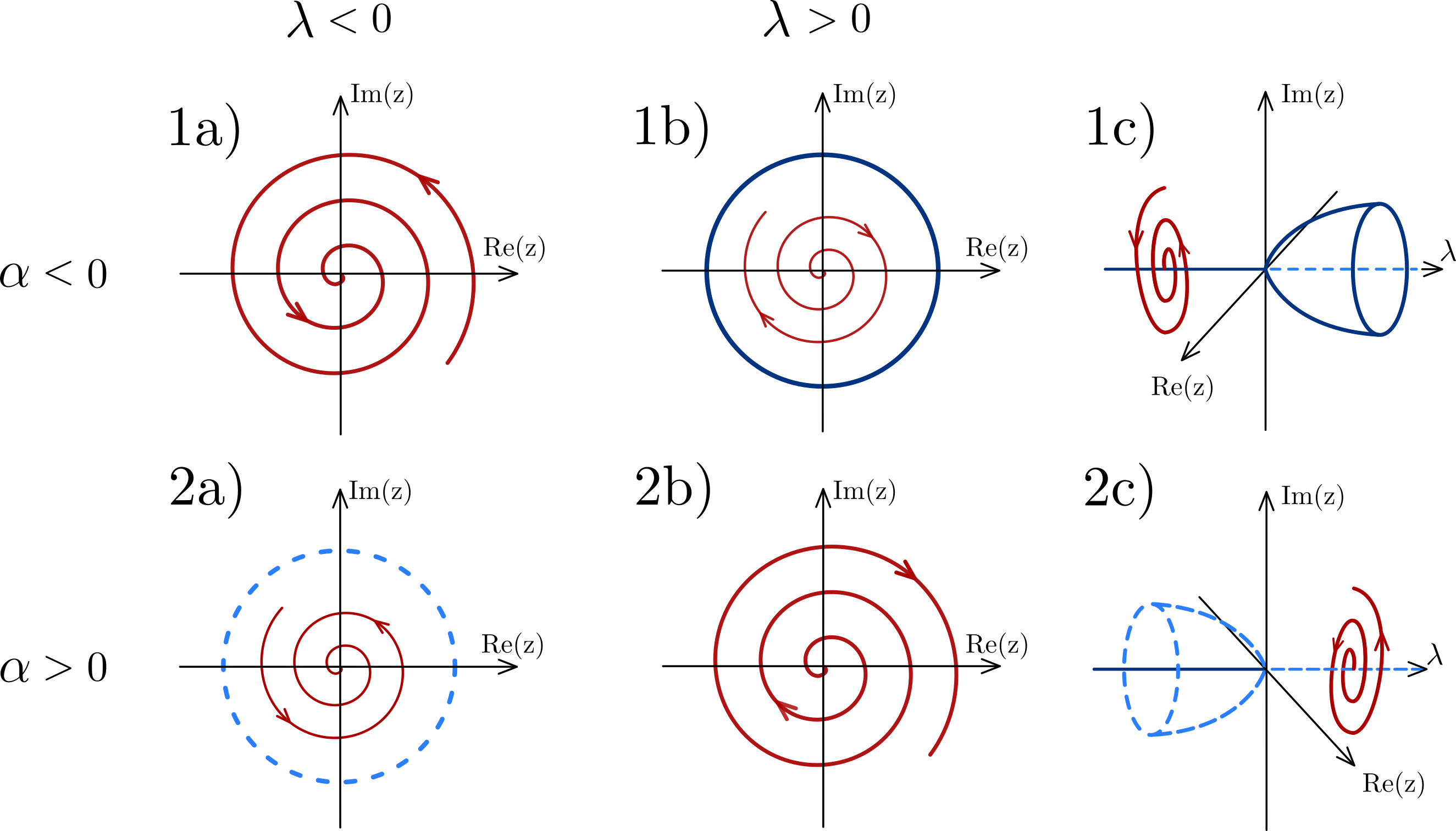 The limit cycle is orbitally stable if the first Lyapunov coefficient is negative, and if Then the bifurcation is said to be supercritical. Otherwise it is unstable and the bifurcation is subcritical.
If is negative then there is a stable limit cycle for
:
where
:
This is the supercritical regime.
If is positive then there is an unstable limit cycle for The bifurcation is said to be subcritical. This classification into sub and super-critical bifurcations is analogous to that of the
The limit cycle is orbitally stable if the first Lyapunov coefficient is negative, and if Then the bifurcation is said to be supercritical. Otherwise it is unstable and the bifurcation is subcritical.
If is negative then there is a stable limit cycle for
:
where
:
This is the supercritical regime.
If is positive then there is an unstable limit cycle for The bifurcation is said to be subcritical. This classification into sub and super-critical bifurcations is analogous to that of the
MIT OpenCourseWare Consider a system defined by , where is smooth and is a parameter. The parameter should be written so that as increases from below zero to above zero, the origin turns from a spiral sink to a spiral source. A linear transform of parameters may be needed to place the equation into this form. For , a perturbative expansion is performed using two-timing: : where is "slow-time" (thus "two-timing"), and are functions of . By an argument of harmonic balance (see for details), one may use . Placing the perturbative expansion for into , and keeping terms up to the produces three ordinary differential equations in . The first equation is of form , which is solved by The are "slowly varying" functions of . Inserting this into the second equation allows it to be solved for . Then plugging the solutions for into the third equation, an equation of form is obtained, with the right-hand-side a sum of trigonometric terms. Of these terms, the "resonance term", the one containing must be set to zero. This is the same idea as in the
File:Hopf_and_homoclinic_bifurcation.gif, A Hopf bifurcation occurs in the system and , when , around the origin. A homoclinic bifurcation occurs around .
File:Hopf_and_homoclinic_bifurcation_2.gif, A detailed view of the homoclinic bifurcation.
File:Hopf_bifurcation,_with_limit_cycle_up_to_order_3-2..gif, As increases from zero, a stable limit cycle emerges from the origin via Hopf bifurcation. The limit cycle is plotted parametrically, up to order .
The Hopf Bifurcation
Andronov–Hopf bifurcation page
at
 In the
In the mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
of dynamical system
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models ...
s and differential equations, a Hopf bifurcation is said to occur when varying a parameter of the system causes the set of solutions (trajectories) to change from being attracted to (or repelled by) a fixed point, and instead become attracted to (or repelled by) an oscillatory, periodic solution. The Hopf bifurcation is a two-dimensional analog of the pitchfork bifurcation
In bifurcation theory, a field within mathematics, a pitchfork bifurcation is a particular type of local bifurcation theory, bifurcation where the system transitions from one fixed point to three fixed points. Pitchfork bifurcations, like Hopf bif ...
.
Many different kinds of systems exhibit Hopf bifurcations, from radio oscillators to railroad bogies. Trailers towed behind automobile
A car, or an automobile, is a motor vehicle with wheels. Most definitions of cars state that they run primarily on roads, Car seat, seat one to eight people, have four wheels, and mainly transport private transport#Personal transport, peopl ...
s become infamously unstable if loaded incorrectly, or if designed with the wrong geometry. This offers a gut-sense intuitive example of a Hopf bifurcation in the ordinary world, where stable motion becomes unstable and oscillatory as a parameter is varied.
The general theory of how the solution sets of dynamical systems change in response to changes of parameters is called bifurcation theory
Bifurcation theory is the Mathematics, mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential e ...
; the term ''bifurcation'' arises, as the set of solutions typically split into several classes. Stability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions. The heat equation, for example, is a stable partial differ ...
pursues the general theory of stability in mechanical, electronic and biological systems.
The conventional approach to locating Hopf bifurcations is to work with the Jacobian matrix
In vector calculus, the Jacobian matrix (, ) of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. If this matrix is square, that is, if the number of variables equals the number of component ...
associated with the system of differential equations. When this matrix has a pair of complex-conjugate eigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
s that cross the imaginary axis as a parameter is varied, that point is the bifurcation. That crossing is associated with a stable fixed point "bifurcating" into a limit cycle
In mathematics, in the study of dynamical systems with two-dimensional phase space, a limit cycle is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity o ...
.
A Hopf bifurcation is also known as a Poincaré–Andronov–Hopf bifurcation, named after Henri Poincaré
Jules Henri Poincaré (, ; ; 29 April 185417 July 1912) was a French mathematician, Theoretical physics, theoretical physicist, engineer, and philosophy of science, philosopher of science. He is often described as a polymath, and in mathemati ...
, Aleksandr Andronov and Eberhard Hopf
Eberhard Frederich Ferdinand Hopf (April 4, 1902 in Salzburg, Austria-Hungary – July 24, 1983 in Bloomington, Indiana, USA) was a German mathematician and astronomer, one of the founding fathers of ergodic theory and a pioneer of bifurcation the ...
.
Overview
Hopf bifurcations occur in a large variety of dynamical systems described by differential equations. Near such a bifurcation, a two-dimensional subset of the dynamical system is approximated by a normal form, canonically expressed as the following time-dependent differential equation: : Here is the dynamical variable; it is a complex number. The parameter is real, and is a complex parameter. The number is called the first Lyapunov coefficient. The above has a simple exact solution, given below. This solution exhibits two distinct behaviors, depending on whether or . This change of behavior, as a function of is termed the "Hopf bifurcation". The study of Hopf bifurcations is not so much the study of the above and its solution, as it is the study of how such two-dimensional subspaces can be identified and mapped onto this normal form. One approach is to examine theeigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
s of the Jacobian matrix
In vector calculus, the Jacobian matrix (, ) of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. If this matrix is square, that is, if the number of variables equals the number of component ...
of the differential equations as a parameter is varied near the bifurcation point.
Exact solution
The normal form is effectively the Stuart–Landau equation, written with a different parameterization. It has a simple exact solution in polar coordinates. Writing and considering the real and imaginary parts as distinct, one obtains a pair of ordinary differential equations: : and : The first equation has the trivial solution : The second equation can be solved by observing that it is linear in . That is, : which is just the shifted exponential equation. Re-arranging gives the generic solution : Depending on the sign of and , the trajectory of a point can be seen to spiral in to the origin, spiral out to infinity, or to approach alimit cycle
In mathematics, in the study of dynamical systems with two-dimensional phase space, a limit cycle is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity o ...
.
Supercritical and subcritical Hopf bifurcations
 The limit cycle is orbitally stable if the first Lyapunov coefficient is negative, and if Then the bifurcation is said to be supercritical. Otherwise it is unstable and the bifurcation is subcritical.
If is negative then there is a stable limit cycle for
:
where
:
This is the supercritical regime.
If is positive then there is an unstable limit cycle for The bifurcation is said to be subcritical. This classification into sub and super-critical bifurcations is analogous to that of the
The limit cycle is orbitally stable if the first Lyapunov coefficient is negative, and if Then the bifurcation is said to be supercritical. Otherwise it is unstable and the bifurcation is subcritical.
If is negative then there is a stable limit cycle for
:
where
:
This is the supercritical regime.
If is positive then there is an unstable limit cycle for The bifurcation is said to be subcritical. This classification into sub and super-critical bifurcations is analogous to that of the pitchfork bifurcation
In bifurcation theory, a field within mathematics, a pitchfork bifurcation is a particular type of local bifurcation theory, bifurcation where the system transitions from one fixed point to three fixed points. Pitchfork bifurcations, like Hopf bif ...
.
Jacobian
The Hopf bifurcation can be understood by examining theeigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
s of the Jacobian matrix
In vector calculus, the Jacobian matrix (, ) of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. If this matrix is square, that is, if the number of variables equals the number of component ...
for the normal form. This is most readily done by re-writing the normal form in Cartesian coordinates . It then has the form
:
where the shorthand and is used. The Jacobian is
:
This is a bit odious to compute:
:
The stable point was previously identified to be located at , at which location the Jacobian takes the particularly simple form:
:
The corresponding characteristic polynomial
In linear algebra, the characteristic polynomial of a square matrix is a polynomial which is invariant under matrix similarity and has the eigenvalues as roots. It has the determinant and the trace of the matrix among its coefficients. The ...
is
:
which has solutions
:
Here, is a pair of complex conjugate eigenvalues of the Jacobian. When the parameter is negative, the real part of the eigenvalues is (obviously) negative. As the parameter crosses zero, the real part vanishes: this is the Hopf bifurcation. As previously seen, the limit cycle arises as goes positive.
All Hopf bifurcations have this general form: the Jacobian matrix has a pair of complex-conjugate eigenvalues that cross the imaginary axis as the pertinent parameter is varied.
Linearization
The above computation of the Jacobian can be significantly simplified by working in thetangent plane
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points o ...
, tangent to the stable point. The stable point is located at and so one can "linearize" the differential equation by dropping all terms that are higher than linear order. This gives
:
The Jacobian is computed exactly as before; nothing has changed, except to make the calculations simpler. The linearized differential equation can be recognized as being given by a Lie derivative
In differential geometry, the Lie derivative ( ), named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a tensor field (including scalar functions, vector fields and one-forms), along the flow defined by another vector fi ...
defined on the tangent bundle
A tangent bundle is the collection of all of the tangent spaces for all points on a manifold, structured in a way that it forms a new manifold itself. Formally, in differential geometry, the tangent bundle of a differentiable manifold M is ...
. Because all cotangent bundles are always symplectic manifold
In differential geometry, a subject of mathematics, a symplectic manifold is a smooth manifold, M , equipped with a closed nondegenerate differential 2-form \omega , called the symplectic form. The study of symplectic manifolds is called sy ...
s, it is common to formulate bifurcation theory in terms of symplectic geometry
Symplectic geometry is a branch of differential geometry and differential topology that studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form. Symplectic geometry has its origins in the ...
.Abraham, R.; Marsden, J. E. (2008). Foundations of Mechanics: A Mathematical Exposition of Classical Mechanics with an Introduction to the Qualitative Theory of Dynamical Systems (2nd ed.). AMS Chelsea Publishing. ISBN 978-0-8218-4438-0.
Examples
Hopf bifurcations occur in the Lotka–Volterra model of predator–prey interaction (known as paradox of enrichment), theHodgkin–Huxley model
The Hodgkin–Huxley model, or conductance-based model, is a mathematical model that describes how action potentials in neurons are initiated and propagated. It is a set of nonlinear differential equations that approximates the electrical engine ...
for nerve membrane potential, the Selkov model of glycolysis
Glycolysis is the metabolic pathway that converts glucose () into pyruvic acid, pyruvate and, in most organisms, occurs in the liquid part of cells (the cytosol). The Thermodynamic free energy, free energy released in this process is used to form ...
, the Belousov–Zhabotinsky reaction, the Lorenz attractor, the Brusselator, the delay differential equation
In mathematics, delay differential equations (DDEs) are a type of differential equation in which the derivative of the unknown function at a certain time is given in terms of the values of the function at previous times.
DDEs are also called tim ...
and in classical electromagnetism
Classical electromagnetism or classical electrodynamics is a branch of physics focused on the study of interactions between electric charges and electrical current, currents using an extension of the classical Newtonian model. It is, therefore, a ...
. Hopf bifurcations have also been shown to occur in fission waves.
The Selkov model is
:
The figure shows a phase portrait illustrating the Hopf bifurcation in the Selkov model.For detailed derivation, see
In railway vehicle systems, Hopf bifurcation analysis is notably important. Conventionally a railway vehicle's stable motion at low speeds crosses over to unstable at high speeds. One aim of the nonlinear analysis of these systems is to perform an analytical investigation of bifurcation, nonlinear lateral stability and hunting behavior of rail vehicles on a tangent track, which uses the Bogoliubov method.
Geometric interpretation
The benefit of the abstract formulation in terms of symplectic geometry is that it enables a geometric intuition into what otherwise seem to be complicated dynamical systems. Consider the space of all possible solutions (point trajectories) to some set of differential equations. The tangent vectors to these solutions lie in thephase space
The phase space of a physical system is the set of all possible physical states of the system when described by a given parameterization. Each possible state corresponds uniquely to a point in the phase space. For mechanical systems, the p ...
for that system; more formally, in the tangent bundle. The phase space can be divided into three parts: the stable manifold
In mathematics, and in particular the study of dynamical systems, the idea of ''stable and unstable sets'' or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repell ...
, the unstable manifold
In mathematics, and in particular the study of dynamical systems, the idea of ''stable and unstable sets'' or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repell ...
, and the center manifold
In the mathematics of evolving systems, the concept of a center manifold was originally developed to determine stability of degenerate equilibria. Subsequently, the concept of center manifolds was realised to be fundamental to mathematical modellin ...
. The stable manifold consists of all of the tangent vector fields that, upon integration, approach the limit point or limit cycle. The unstable manifold consist of those vector fields that point away from the limit-point/limit cycle. The center manifold consists of the points on the limit, together with their tangent vectors.
The Hopf bifurcation is a rearrangement of these manifolds, as parameters are varied. For the normal form, the phase space is four-dimensional: the two coordinates and the two velocities When (and ) the entire (four-dimensional) space of solutions belongs to the stable manifold. As is varied, the center manifold changes from a point to a circle. As is varied, the stable manifold flips to become unstable.
In a general setting, the abstraction allows a four-dimensional subspace to be isolated from the full system, and then, as parameters are varied, all changes to the overall geometry are isolated to that four-dimensional subspace.
Formal definition of a Hopf bifurcation
The appearance or the disappearance of a periodic orbit through a local change in the stability properties of a fixed point is known as the Hopf bifurcation. The following theorem works for fixed points with one pair of conjugate nonzero purely imaginaryeigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
s. It tells the conditions under which this bifurcation phenomenon occurs.
Theorem (see section 11.2 of ). Let be the Jacobian of a continuous parametric dynamical system
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models ...
evaluated at a stable point. Suppose that all eigenvalues of have negative real part except for one conjugate pair, varying as for some function of the parameters. A Hopf bifurcation arises when this eigenvalue pair cross the imaginary axis. This occurs as changes from negative to positive as the system parameters are varied.
Routh–Hurwitz criterion
The Routh–Hurwitz criterion (section I.13 of ) gives necessary conditions for a Hopf bifurcation to occur.Sturm series
Let be Sturm series associated to acharacteristic polynomial
In linear algebra, the characteristic polynomial of a square matrix is a polynomial which is invariant under matrix similarity and has the eigenvalues as roots. It has the determinant and the trace of the matrix among its coefficients. The ...
. They can be written in the form:
:
The coefficients for in correspond to what is called Hurwitz determinants. Their definition is related to the associated Hurwitz matrix.
Propositions
Proposition 1. If all the Hurwitz determinants are positive, apart perhaps then the associated Jacobian has no pure imaginary eigenvalues. Proposition 2. If all Hurwitz determinants (for all in are positive, and then all the eigenvalues of the associated Jacobian have negative real parts except a purely imaginary conjugate pair. The conditions that we are looking for so that a Hopf bifurcation occurs (see theorem above) for a parametric continuous dynamical system are given by this last proposition.Example
Consider the classical Van der Pol oscillator written with ordinary differential equations: : The Jacobian matrix associated to this system is : The characteristic polynomial (in ) of the Jacobian at the stable point is : The associated Sturm series is : with coefficients The Sturm polynomials can be written as (here ): : For the Van der Pol oscillator, the coefficients are : A Hopf bifurcation can occur when proposition 2 is satisfied; in the present case, proposition 2 requires that : Clearly, the first and third conditions are satisfied; the second condition states that a Hopf bifurcation occurs for the Van der Pol oscillator when .Serial expansion method
The serial expansion method provides a way for obtaining explicit solutions containing a Hopf bifurcation by means of a perturbative expansion in the order parameter.18.385J / 2.036J Nonlinear Dynamics and Chaos Fall 2014: Hopf BifurcationsMIT OpenCourseWare Consider a system defined by , where is smooth and is a parameter. The parameter should be written so that as increases from below zero to above zero, the origin turns from a spiral sink to a spiral source. A linear transform of parameters may be needed to place the equation into this form. For , a perturbative expansion is performed using two-timing: : where is "slow-time" (thus "two-timing"), and are functions of . By an argument of harmonic balance (see for details), one may use . Placing the perturbative expansion for into , and keeping terms up to the produces three ordinary differential equations in . The first equation is of form , which is solved by The are "slowly varying" functions of . Inserting this into the second equation allows it to be solved for . Then plugging the solutions for into the third equation, an equation of form is obtained, with the right-hand-side a sum of trigonometric terms. Of these terms, the "resonance term", the one containing must be set to zero. This is the same idea as in the
Poincaré–Lindstedt method
In perturbation theory, the Poincaré–Lindstedt method or Lindstedt–Poincaré method is a technique for uniformly approximating periodic solutions to ordinary differential equations, when regular perturbation approaches fail. The method remove ...
. This provides two ordinary differential equations for , allowing one to solve for the equilibrium value of , as well as its stability.
Example of serial expansion
Consider the system defined by : This system has an equilibrium point at origin. When increases from negative to positive, the origin turns from a stable spiral point to an unstable spiral point. Eliminating from the equations gives a singe second-order differential equation : The perturbative expansion to be performed is : with : Expanding up to order results in : The first equation has the solution : Here are respectively the "slow-varying amplitude" and "slow-varying phase" of the simple oscillation. The second equation has solution : where are also slow-varying amplitude and phase. The and terms can be absorbed into and equivalently, can be set without loss of generality. To demonstrate this, the perturbative expansion is written as : Basic trigonometry allows the two cosines to be merged into one: : for some and But this has exactly the same form as Thus, the term can be eliminated by redefining to be and to be The solution to the second equation is thus : Plugging through the third equation gives : Eliminating the resonance term gives : where the prime denotes differentiation by the slow time The first equation shows that is a stable equilibrium. The Hopf bifurcation creates an attracting (rather than repelling) limit cycle. Plugging in gives . The time coordinate can be shifted so that . The third equation becomes : giving a solution : Plugging in back to the expressions for gives : Plugging these back to yields the serial expansion of as well, up to order . After writing the solution is : and : This provides a parametric equation for the limit cycle. This is plotted in the illustration on the right.See also
* Reaction–diffusion systemsReferences
Further reading
* * * * *External links
{{commons category, Hopf bifurcationsThe Hopf Bifurcation
Andronov–Hopf bifurcation page
at
Scholarpedia
''Scholarpedia'' is an English-language wiki-based online encyclopedia with features commonly associated with Open access (publishing), open-access online academic journals, which aims to have quality content in science and medicine.
''Scholarpe ...
Bifurcation theory
Circuit theorems