Fresnel Integrals on:
[Wikipedia]
[Google]
[Amazon]
250px,
Plots of and . The maximum of is about . If the integrands of and were defined using instead of , then the image would be scaled vertically and horizontally (see below).
The Fresnel integrals and are two
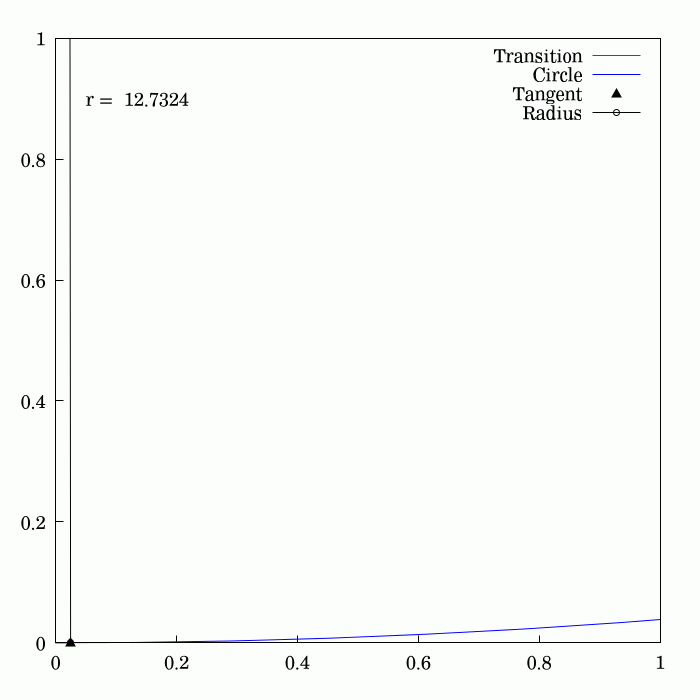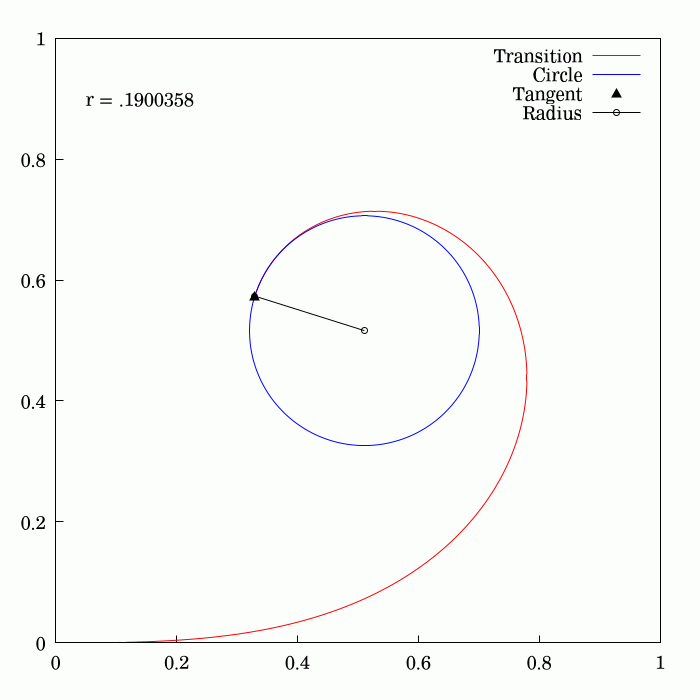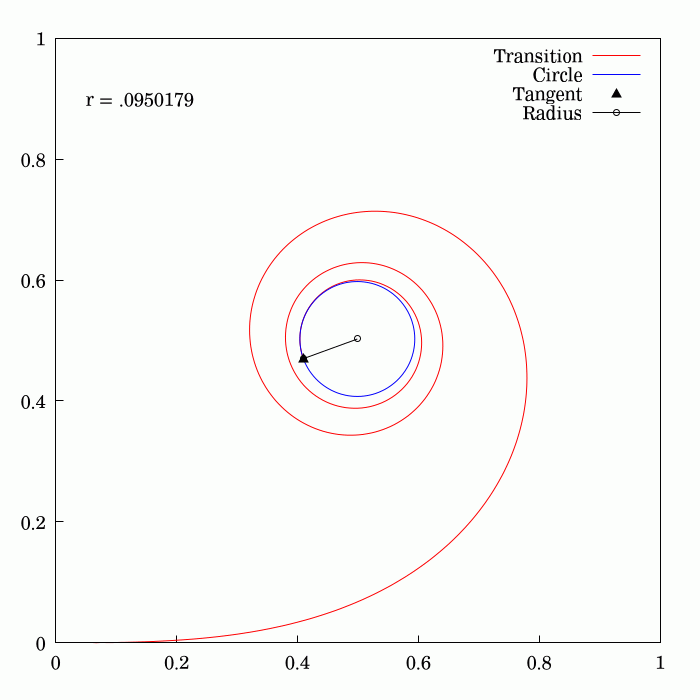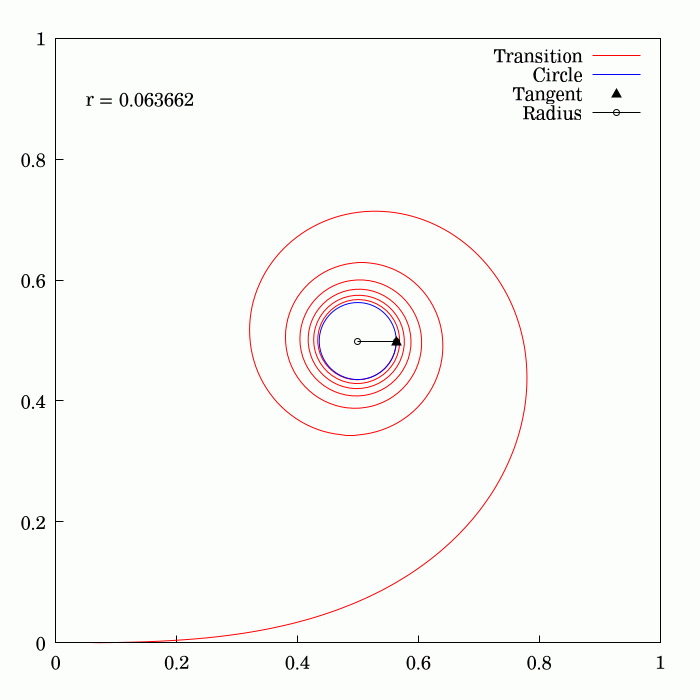 The Euler spiral, also known as a Cornu spiral or clothoid, is the curve generated by a
The Euler spiral, also known as a Cornu spiral or clothoid, is the curve generated by a
 Using the power series expansions above, the Fresnel integrals can be extended to the domain of
Using the power series expansions above, the Fresnel integrals can be extended to the domain of  or
or
File:Plot of the Fresnel integral function S(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D.svg, Plot of the Fresnel integral function S(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
File:Plot of the Fresnel integral function C(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D.svg, Plot of the Fresnel integral function C(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
File:Plot of the Fresnel auxillary function G(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D.svg, Plot of the Fresnel auxiliary function G(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
File:Plot of the Fresnel auxillary function F(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D.svg, Plot of the Fresnel auxiliary function F(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Cephes
free/open-source C++/C code to compute Fresnel integrals among other special functions. Used in
Faddeeva Package
free/open-source C++/C code to compute complex error functions (from which the Fresnel integrals can be obtained), with wrappers for Matlab, Python, and other languages. * * * * {{Nonelementary Integral Integral calculus Spirals Physical optics Special functions Special hypergeometric functions Analytic functions Diffraction
transcendental function
In mathematics, a transcendental function is an analytic function that does not satisfy a polynomial equation whose coefficients are functions of the independent variable that can be written using only the basic operations of addition, subtraction ...
s named after Augustin-Jean Fresnel
Augustin-Jean Fresnel (10 May 1788 – 14 July 1827) was a French civil engineer and physicist whose research in optics led to the almost unanimous acceptance of the wave theory of light, excluding any remnant of Isaac Newton, Newton's c ...
that are used in optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes t ...
and are closely related to the error function
In mathematics, the error function (also called the Gauss error function), often denoted by , is a function \mathrm: \mathbb \to \mathbb defined as:
\operatorname z = \frac\int_0^z e^\,\mathrm dt.
The integral here is a complex Contour integrat ...
(). They arise in the description of near-field Fresnel diffraction
In optics, the Fresnel diffraction equation for near-field diffraction is an approximation of the Kirchhoff's diffraction formula, Kirchhoff–Fresnel diffraction that can be applied to the propagation of waves in the near and far field, near fi ...
phenomena and are defined through the following integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental oper ...
representations:
The parametric curve
In mathematics, a parametric equation expresses several quantities, such as the coordinates of a point (mathematics), point, as Function (mathematics), functions of one or several variable (mathematics), variables called parameters.
In the case ...
is the Euler spiral
An Euler spiral is a curve whose curvature changes linearly with its curve length (the curvature of a circular curve is equal to the reciprocal of the radius). This curve is also referred to as a clothoid or Cornu spiral.Levien, Raph"The Euler spi ...
or clothoid, a curve whose curvature varies linearly with arclength.
The term Fresnel integral may also refer to the complex definite integral
where is real and positive; this can be evaluated by closing a contour in the complex plane and applying Cauchy's integral theorem.
Definition
250px, Fresnel integrals with arguments instead of converge to instead of . The Fresnel integrals admit the followingMaclaurin series
Maclaurin or MacLaurin is a surname. Notable people with the surname include:
* Colin Maclaurin (1698–1746), Scottish mathematician
* Normand MacLaurin (1835–1914), Australian politician and university administrator
* Henry Normand MacLaurin ...
that converge for all :
Some widely used tables use instead of for the argument of the integrals defining and . This changes their limits at infinity from to and the arc length for the first spiral turn from to 2 (at ). These alternative functions are usually known as normalized Fresnel integrals.
Euler spiral
 The Euler spiral, also known as a Cornu spiral or clothoid, is the curve generated by a
The Euler spiral, also known as a Cornu spiral or clothoid, is the curve generated by a parametric plot
In mathematics, a parametric equation expresses several quantities, such as the coordinates of a point, as functions of one or several variables called parameters.
In the case of a single parameter, parametric equations are commonly used to ...
of against . The Euler spiral was first studied in the mid 18th century by Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...
in the context of Euler–Bernoulli beam theory
Euler–Bernoulli beam theory (also known as engineer's beam theory or classical beam theory) is a simplification of the linear elasticity, linear theory of elasticity which provides a means of calculating the load-carrying and Deflection (engine ...
. A century later, Marie Alfred Cornu
Marie Alfred Cornu (; 6 March 1841 – 12 April 1902) was a French physicist and professor of École polytechnique. The French generally refer to him as Alfred Cornu. The Cornu spiral, a graphical device for the computation of light intensities ...
constructed the same spiral as a nomogram
A nomogram (), also called a nomograph, alignment chart, or abac, is a graphical Analog computer, calculating device, a two-dimensional diagram designed to allow the approximate graphical computation of a Function (mathematics), mathematical fu ...
for diffraction computations.
From the definitions of Fresnel integrals, the infinitesimal
In mathematics, an infinitesimal number is a non-zero quantity that is closer to 0 than any non-zero real number is. The word ''infinitesimal'' comes from a 17th-century Modern Latin coinage ''infinitesimus'', which originally referred to the " ...
s and are thus:
Thus the length of the spiral measured from the origin
Origin(s) or The Origin may refer to:
Arts, entertainment, and media
Comics and manga
* ''Origin'' (comics), a Wolverine comic book mini-series published by Marvel Comics in 2002
* ''The Origin'' (Buffy comic), a 1999 ''Buffy the Vampire Sl ...
can be expressed as
That is, the parameter is the curve length measured from the origin , and the Euler spiral has infinite
Infinite may refer to:
Mathematics
*Infinite set, a set that is not a finite set
*Infinity, an abstract concept describing something without any limit
Music Performers
*Infinite (group), a South Korean boy band
*Infinite (rapper), Canadian ra ...
length. The vector , where , also expresses the unit
Unit may refer to:
General measurement
* Unit of measurement, a definite magnitude of a physical quantity, defined and adopted by convention or by law
**International System of Units (SI), modern form of the metric system
**English units, histo ...
tangent vector
In mathematics, a tangent vector is a vector that is tangent to a curve or surface at a given point. Tangent vectors are described in the differential geometry of curves in the context of curves in R''n''. More generally, tangent vectors are ...
along the spiral. Since is the curve length, the curvature can be expressed as
Thus the rate of change of curvature with respect to the curve length is
An Euler spiral has the property that its curvature
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or su ...
at any point is proportional to the distance along the spiral, measured from the origin. This property makes it useful as a transition curve in highway and railway engineering: if a vehicle follows the spiral at unit speed, the parameter in the above derivatives also represents the time. Consequently, a vehicle following the spiral at constant speed will have a constant rate of angular acceleration
In physics, angular acceleration (symbol α, alpha) is the time rate of change of angular velocity. Following the two types of angular velocity, ''spin angular velocity'' and ''orbital angular velocity'', the respective types of angular accele ...
.
Sections from Euler spirals are commonly incorporated into the shape of rollercoaster
A roller coaster is a type of amusement ride employing a form of elevated railroad track that carries passengers on a train through tight turns, steep slopes, and other elements, usually designed to produce a thrilling experience, though some r ...
loops to make what are known as clothoid loops.
Properties
and areodd function
In mathematics, an even function is a real function such that f(-x)=f(x) for every x in its domain. Similarly, an odd function is a function such that f(-x)=-f(x) for every x in its domain.
They are named for the parity of the powers of the ...
s of ,
which can be readily seen from the fact that their power series expansions have only odd-degree terms, or alternatively because they are antiderivatives of even functions that also are zero at the origin.
Asymptotics of the Fresnel integrals as are given by the formulas:
complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s, where they become entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic on the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any ...
s of the complex variable .
The Fresnel integrals can be expressed using the error function
In mathematics, the error function (also called the Gauss error function), often denoted by , is a function \mathrm: \mathbb \to \mathbb defined as:
\operatorname z = \frac\int_0^z e^\,\mathrm dt.
The integral here is a complex Contour integrat ...
as follows: Limits as approaches infinity
The integrals defining and cannot be evaluated in the closed form in terms ofelementary function
In mathematics, an elementary function is a function of a single variable (typically real or complex) that is defined as taking sums, products, roots and compositions of finitely many polynomial, rational, trigonometric, hyperbolic, a ...
s, except in special cases. The limits
Limit or Limits may refer to:
Arts and media
* ''Limit'' (manga), a manga by Keiko Suenobu
* ''Limit'' (film), a South Korean film
* Limit (music), a way to characterize harmony
* "Limit" (song), a 2016 single by Luna Sea
* "Limits", a 2009 ...
of these functions as goes to infinity are known:
This can be derived with any one of several methods. One of themAnother method based on parametric integration is described for example in . uses a contour integral
In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.
Contour integration is closely related to the calculus of residues, a method of complex analysis.
...
of the function around the boundary of the sector
Sector may refer to:
Places
* Sector, West Virginia, U.S.
Geometry
* Circular sector, the portion of a disc enclosed by two radii and a circular arc
* Hyperbolic sector, a region enclosed by two radii and a hyperbolic arc
* Spherical sector, a po ...
-shaped region in the complex plane
In mathematics, the complex plane is the plane (geometry), plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal -axis, called the real axis, is formed by the real numbers, and the vertical -axis, call ...
formed by the positive -axis, the bisector of the first quadrant with , and a circular arc of radius centered at the origin.
As goes to infinity, the integral along the circular arc tends to
where polar coordinates were used and Jordan's inequality
In mathematics, Jordan's inequality, named after Camille Jordan, states that
: \fracx\leq \sin(x) \leq x\textx \in \left ,\frac\right
It can be proven through the geometry of circles (see drawing).Feng Yuefeng, Proof without words: Jordan`s ...
was utilised for the second inequality. The integral along the real axis tends to the half Gaussian integral
The Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function f(x) = e^ over the entire real line. Named after the German mathematician Carl Friedrich Gauss, the integral is
\int_^\infty e^\,dx = \s ...
Note too that because the integrand is an entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic on the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any ...
on the complex plane, its integral along the whole contour is zero. Overall, we must have
where denotes the bisector of the first quadrant, as in the diagram. To evaluate the left hand side, parametrize the bisector as
where ranges from 0 to . Note that the square of this expression is just . Therefore, substitution gives the left hand side as
Using Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for ...
to take real and imaginary parts of gives this as
where we have written to emphasize that the original Gaussian integral's value is completely real with zero imaginary part. Letting
and then equating real and imaginary parts produces the following system of two equations in the two unknowns and :
Solving this for and gives the desired result.
Generalization
The integral is aconfluent hypergeometric function
In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular s ...
and also an incomplete gamma function
In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems such as certain integrals.
Their respective names stem from their integral definitions, whic ...
which reduces to Fresnel integrals if real or imaginary parts are taken:
The leading term in the asymptotic expansion is
and therefore
For , the imaginary part of this equation in particular is
with the left-hand side converging for and the right-hand side being its analytical extension to the whole plane less where lie the poles of .
The Kummer transformation of the confluent hypergeometric function is
with
Numerical approximation
For computation to arbitrary precision, the power series is suitable for small argument. For large argument, asymptotic expansions converge faster. Continued fraction methods may also be used. For computation to particular target precision, other approximations have been developed. Cody developed a set of efficient approximations based on rational functions that give relative errors down to . A FORTRAN implementation of the Cody approximation that includes the values of the coefficients needed for implementation in other languages was published by van Snyder. Boersma developed an approximation with error less than .Applications
The Fresnel integrals were originally used in the calculation of the electromagnetic field intensity in an environment where light bends around opaque objects. More recently, they have been used in the design of highways and railways, specifically their curvature transition zones, seetrack transition curve
A transition curve (also, spiral easement or, simply, spiral) is a spiral-shaped length of highway or track (rail transport), railroad track that is used between sections having different profiles and radii, such as between straightaways (tangen ...
. Other applications are rollercoaster
A roller coaster is a type of amusement ride employing a form of elevated railroad track that carries passengers on a train through tight turns, steep slopes, and other elements, usually designed to produce a thrilling experience, though some r ...
s or calculating the transitions on a velodrome
A velodrome is an arena for track cycling. Modern velodromes feature steeply banked oval tracks, consisting of two 180-degree circular bends connected by two straights. The straights transition to the circular turn through a moderate easement ...
track to allow rapid entry to the bends and gradual exit.
Gallery
See also
*Böhmer integral In mathematics, a Böhmer integral is an integral introduced by generalizing the Fresnel integrals.
There are two versions, given by
\begin
\operatorname(x,\alpha) &= \int_x^\infty t^ \cos(t) \, dt \\ ex\operatorname(x,\alpha) &= \int_x^\infty t^ ...
* Fresnel zone
A Fresnel zone ( ), named after physicist Augustin-Jean Fresnel, is one of a series of confocal prolate ellipsoidal regions of space between and around a transmitter and a receiver. The size of the calculated Fresnel zone at any particular di ...
* Track transition curve
A transition curve (also, spiral easement or, simply, spiral) is a spiral-shaped length of highway or track (rail transport), railroad track that is used between sections having different profiles and radii, such as between straightaways (tangen ...
* Euler spiral
An Euler spiral is a curve whose curvature changes linearly with its curve length (the curvature of a circular curve is equal to the reciprocal of the radius). This curve is also referred to as a clothoid or Cornu spiral.Levien, Raph"The Euler spi ...
* Zone plate
A zone plate is a device used to focus light or other things exhibiting wave character.G. W. Webb, I. V. Minin and O. V. Minin, “Variable Reference Phase in Diffractive Antennas”, ''IEEE Antennas and Propagation Magazine'', vol. 53, no. 2, ...
* Dirichlet integral
In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over the positive real number line.
\int_0 ...
Notes
References
* * * * * * * * * (Uses instead of .) * * * * * *External links
Cephes
free/open-source C++/C code to compute Fresnel integrals among other special functions. Used in
SciPy
SciPy (pronounced "sigh pie") is a free and open-source Python library used for scientific computing and technical computing.
SciPy contains modules for optimization, linear algebra, integration, interpolation, special functions, fast Fourier ...
and ALGLIB
ALGLIB is a cross-platform open source numerical analysis and data processing library. It can be used from several programming languages ( C++, C#, VB.NET, Python, Delphi, Java).
ALGLIB started in 1999 and has a long history of steady developm ...
.Faddeeva Package
free/open-source C++/C code to compute complex error functions (from which the Fresnel integrals can be obtained), with wrappers for Matlab, Python, and other languages. * * * * {{Nonelementary Integral Integral calculus Spirals Physical optics Special functions Special hypergeometric functions Analytic functions Diffraction