Fixed-point Iteration on:
[Wikipedia]
[Google]
[Amazon]
In
 * A first simple and useful example is the Babylonian method for computing the
* A first simple and useful example is the Babylonian method for computing the
 An ''attracting fixed point'' of a function is a fixed point of with a
An ''attracting fixed point'' of a function is a fixed point of with a
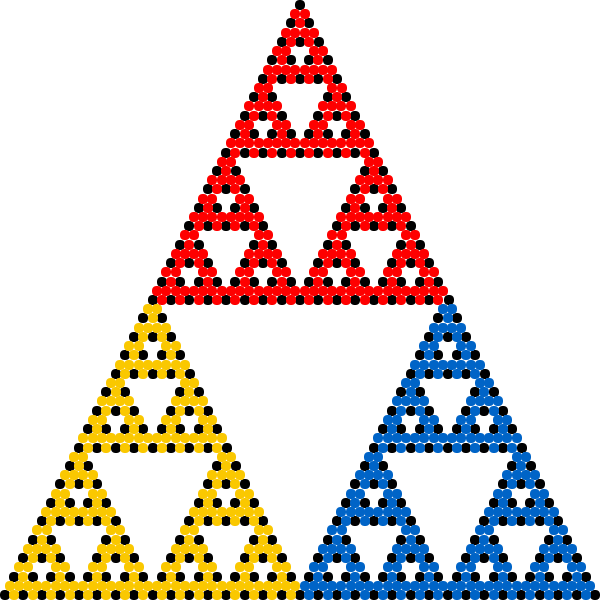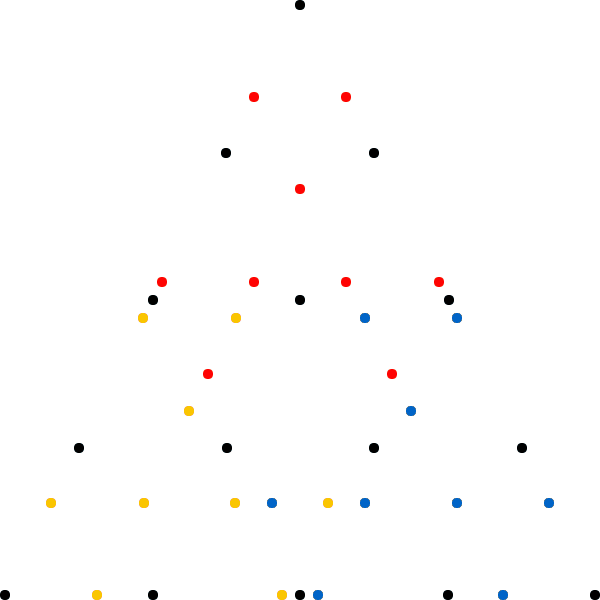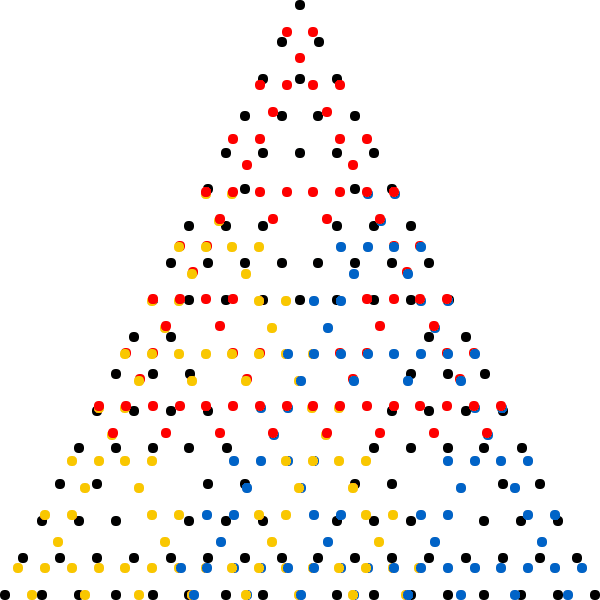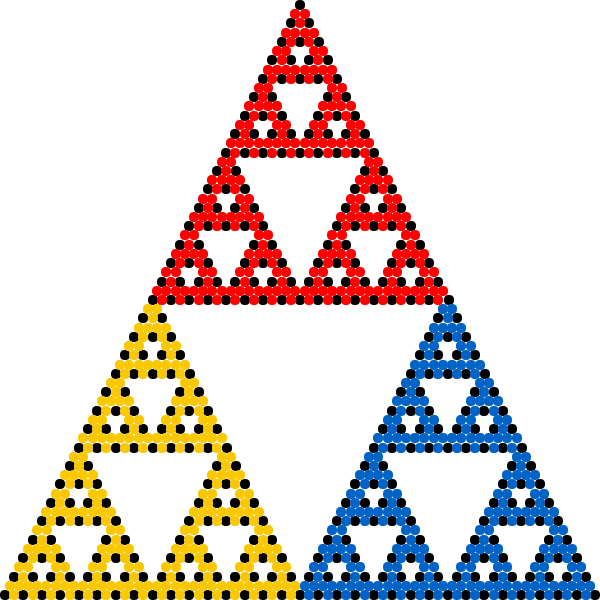 The term ''chaos game'' refers to a method of generating the fixed point of any iterated function system (IFS). Starting with any point , successive iterations are formed as , where is a member of the given IFS randomly selected for each iteration. Hence the chaos game is a randomized fixed-point iteration. The chaos game allows plotting the general shape of a
The term ''chaos game'' refers to a method of generating the fixed point of any iterated function system (IFS). Starting with any point , successive iterations are formed as , where is a member of the given IFS randomly selected for each iteration. Hence the chaos game is a randomized fixed-point iteration. The chaos game allows plotting the general shape of a
Fixed-point algorithms onlineFixed-point iteration online calculator (Mathematical Assistant on Web)
{{root-finding algorithms Root-finding algorithms Iterative methods
numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of ...
, fixed-point iteration is a method of computing fixed points of a function.
More specifically, given a function defined on the real number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every re ...
s with real values and given a point in the domain of , the fixed-point iteration is
which gives rise to the sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is cal ...
of iterated function
In mathematics, an iterated function is a function that is obtained by composing another function with itself two or several times. The process of repeatedly applying the same function is called iteration. In this process, starting from some ...
applications which is hoped to converge to a point . If is continuous, then one can prove that the obtained is a fixed point of , i.e.,
More generally, the function can be defined on any metric space
In mathematics, a metric space is a Set (mathematics), set together with a notion of ''distance'' between its Element (mathematics), elements, usually called point (geometry), points. The distance is measured by a function (mathematics), functi ...
with values in that same space.
Examples
square root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4 ...
of , which consists in taking , i.e. the mean value of and , to approach the limit (from whatever starting point ). This is a special case of Newton's method
In numerical analysis, the Newton–Raphson method, also known simply as Newton's method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots (or zeroes) of a ...
quoted below.
* The fixed-point iteration converges to the unique fixed point of the function for any starting point This example does satisfy (at the latest after the first iteration step) the assumptions of the Banach fixed-point theorem. Hence, the error after n steps satisfies (where we can take , if we start from .) When the error is less than a multiple of for some constant , we say that we have linear convergence. The Banach fixed-point theorem allows one to obtain fixed-point iterations with linear convergence.
* The requirement that is continuous is important, as the following example shows. The iteration converges to 0 for all values of . However, 0 is ''not'' a fixed point of the function as this function is ''not'' continuous at , and in fact has no fixed points.
Attracting fixed points
neighborhood
A neighbourhood (Commonwealth English) or neighborhood (American English) is a geographically localized community within a larger town, city, suburb or rural area, sometimes consisting of a single street and the buildings lining it. Neigh ...
of "close enough" points around such that for any value of in , the fixed-point iteration sequence
is contained in and converges to . The basin of attraction of is the largest such neighborhood .
The natural cosine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that ...
function ("natural" means in radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...
s, not degrees or other units) has exactly one fixed point, and that fixed point is attracting. In this case, "close enough" is not a stringent criterion at all—to demonstrate this, start with ''any'' real number and repeatedly press the ''cos'' key on a calculator (checking first that the calculator is in "radians" mode). It eventually converges to the Dottie number (about 0.739085133), which is a fixed point. That is where the graph of the cosine function intersects the line .
Not all fixed points are attracting. For example, 0 is a fixed point of the function , but iteration of this function for any value other than zero rapidly diverges. We say that the fixed point of is repelling.
An attracting fixed point is said to be a ''stable fixed point'' if it is also Lyapunov stable.
A fixed point is said to be a ''neutrally stable fixed point'' if it is Lyapunov stable but not attracting. The center of a linear homogeneous differential equation of the second order is an example of a neutrally stable fixed point.
Multiple attracting points can be collected in an ''attracting fixed set''.
Banach fixed-point theorem
The Banach fixed-point theorem gives a sufficient condition for the existence of attracting fixed points. A contraction mapping function defined on acomplete metric space
In mathematical analysis, a metric space is called complete (or a Cauchy space) if every Cauchy sequence of points in has a limit that is also in .
Intuitively, a space is complete if there are no "points missing" from it (inside or at the bou ...
has precisely one fixed point, and the fixed-point iteration is attracted towards that fixed point for any initial guess in the domain of the function. Common special cases are that (1) is defined on the real line with real values and is Lipschitz continuous
In mathematical analysis, Lipschitz continuity, named after Germany, German mathematician Rudolf Lipschitz, is a strong form of uniform continuity for function (mathematics), functions. Intuitively, a Lipschitz continuous function is limited in h ...
with Lipschitz constant , and (2) the function is continuously differentiable in an open neighbourhood of a fixed point , and .
Although there are other fixed-point theorems, this one in particular is very useful because not all fixed-points are attractive. When constructing a fixed-point iteration, it is very important to make sure it converges to the fixed point. We can usually use the Banach fixed-point theorem to show that the fixed point is attractive.
Attractors
Attracting fixed points are a special case of a wider mathematical concept of attractors. Fixed-point iterations are a discretedynamical system
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models ...
on one variable. Bifurcation theory studies dynamical systems and classifies various behaviors such as attracting fixed points, periodic orbits, or strange attractor
In the mathematics, mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor va ...
s. An example system is the logistic map.
Iterative methods
In computational mathematics, an iterative method is a mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the n-th approximation is derived from the previous ones. Convergent fixed-point iterations are mathematically rigorous formalizations of iterative methods.Iterative method examples
Convergence acceleration
The speed of convergence of the iteration sequence can be increased by using a convergence acceleration method such as Anderson acceleration and Aitken's delta-squared process. The application of Aitken's method to fixed-point iteration is known as Steffensen's method, and it can be shown that Steffensen's method yields a rate of convergence that is at least quadratic.Chaos game
 The term ''chaos game'' refers to a method of generating the fixed point of any iterated function system (IFS). Starting with any point , successive iterations are formed as , where is a member of the given IFS randomly selected for each iteration. Hence the chaos game is a randomized fixed-point iteration. The chaos game allows plotting the general shape of a
The term ''chaos game'' refers to a method of generating the fixed point of any iterated function system (IFS). Starting with any point , successive iterations are formed as , where is a member of the given IFS randomly selected for each iteration. Hence the chaos game is a randomized fixed-point iteration. The chaos game allows plotting the general shape of a fractal
In mathematics, a fractal is a Shape, geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scale ...
such as the Sierpinski triangle by repeating the iterative process a large number of times. More mathematically, the iterations converge to the fixed point of the IFS. Whenever belongs to the attractor of the IFS, all iterations stay inside the attractor and, with probability 1, form a dense set
In topology and related areas of mathematics, a subset ''A'' of a topological space ''X'' is said to be dense in ''X'' if every point of ''X'' either belongs to ''A'' or else is arbitrarily "close" to a member of ''A'' — for instance, the ...
in the latter.
See also
*Fixed-point combinator
In combinatory logic for computer science, a fixed-point combinator (or fixpoint combinator) is a higher-order function (i.e., a function which takes a function as argument) that returns some '' fixed point'' (a value that is mapped to itself) of ...
* Cobweb plot
* Markov chain
In probability theory and statistics, a Markov chain or Markov process is a stochastic process describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally ...
* Infinite compositions of analytic functions
In mathematics, infinite Function composition, compositions of analytic functions (ICAF) offer alternative formulations of Generalized continued fraction, analytic continued fractions, series (mathematics), series, product (mathematics), products ...
* Rate of convergence
References
Further reading
* * * * * *External links
Fixed-point algorithms online
{{root-finding algorithms Root-finding algorithms Iterative methods