Euclid's formula

A Pythagorean triple consists of three positive integers , , and , such that . Such a triple is commonly written , a well-known example is . If is a Pythagorean triple, then so is for any positive integer . A triangle whose side lengths are a Pythagorean triple is a right triangle and called a Pythagorean triangle.

A primitive Pythagorean triple is one in which , and are coprime (that is, they have no common divisor larger than 1). For example, is a primitive Pythagorean triple whereas is not. Every Pythagorean triple can be scaled to a unique primitive Pythagorean triple by dividing by their greatest common divisor. Conversely, every Pythagorean triple can be obtained by multiplying the elements of a primitive Pythagorean triple by a positive integer (the same for the three elements).

The name is derived from the Pythagorean theorem, stating that every right triangle has side lengths satisfying the formula $a^2+b^2=c^2$; thus, Pythagorean triples describe the three integer side lengths of a right triangle. However, right triangles with non-integer sides do not form Pythagorean triples. For instance, the triangle with sides $a=b=1$ and $c=\sqrt2$ is a right triangle, but $(1,1,\sqrt2)$ is not a Pythagorean triple because the square root of 2 is not an integer. Moreover, $1$ and $\sqrt2$ do not have an integer common multiple because $\sqrt2$ is irrational.

Pythagorean triples have been known since ancient times. The oldest known record comes from Plimpton 322, a Babylonian clay tablet from about 1800 BC, written in a sexagesimal number system.

When searching for integer solutions, the equation is a Diophantine equation. Thus Pythagorean triples are among the oldest known solutions of a nonlinear Diophantine equation.

Examples

There are 16 primitive Pythagorean triples of numbers up to 100:

Other small Pythagorean triples such as (6, 8, 10) are not listed because they are not primitive; for instance (6, 8, 10) is a multiple of (3, 4, 5).

Each of these points (with their multiples) forms a radiating line in the scatter plot to the right.

Additionally, these are the remaining primitive Pythagorean triples of numbers up to 300:

Generating a triple

Euclid's formula is a fundamental formula for generating Pythagorean triples given an arbitrary pair of integers and with . The formula states that the integers

:$a = m^2 - n^2 ,\ \, b = 2mn ,\ \, c = m^2 + n^2$

form a Pythagorean triple. For example, given

:$m = 2 ,\ \, n = 1$

generate the primitive triple (3,4,5):

:$a = 2^2 - 1^2 = 3 ,\ \, b = 2 \times 2 \times 1 = 4 ,\ \, c = 2^2 + 1^2 = 5.$

The triple generated by Euclid's formula is primitive if and only if and are coprime and exactly one of them is even. When both and are odd, then , , and will be even, and the triple will not be primitive; however, dividing , , and by 2 will yield a primitive triple when and are coprime.

''Every'' primitive triple arises (after the exchange of and , if is even) from a ''unique pair'' of coprime numbers , , one of which is even. It follows that there are infinitely many primitive Pythagorean triples. This relationship of , and to and from Euclid's formula is referenced throughout the rest of this article.

Despite generating all primitive triples, Euclid's formula does not produce all triples—for example, (9, 12, 15) cannot be generated using integer and . This can be remedied by inserting an additional parameter to the formula. The following will generate all Pythagorean triples uniquely:

:$a = k\cdot(m^2 - n^2) ,\ \, b = k\cdot(2mn) ,\ \, c = k\cdot(m^2 + n^2)$

where , , and are positive integers with , and with and coprime and not both odd.

That these formulas generate Pythagorean triples can be verified by expanding using elementary algebra and verifying that the result equals . Since every Pythagorean triple can be divided through by some integer to obtain a primitive triple, every triple can be generated uniquely by using the formula with and to generate its primitive counterpart and then multiplying through by as in the last equation.

Choosing and from certain integer sequences gives interesting results. For example, if and are consecutive Pell numbers, and will differ by 1.

Many formulas for generating triples with particular properties have been developed since the time of Euclid.

Proof of Euclid's formula

That satisfaction of Euclid's formula by ''a, b, c'' is sufficient for the triangle to be Pythagorean is apparent from the fact that for positive integers and , , the , , and given by the formula are all positive integers, and from the fact that

:$a^2+b^2 = (m^2 - n^2)^2 + (2mn)^2 = (m^2 + n^2)^2 = c^2.$

A proof of the ''necessity'' that ''a, b, c'' be expressed by Euclid's formula for any primitive Pythagorean triple is as follows. All such primitive triples can be written as where and , , are coprime. Thus , , are pairwise coprime (if a prime number divided two of them, it would be forced also to divide the third one). As and are coprime, at least one of them is odd. If we suppose that is odd, then is even and is odd (if both and were odd, would be even, and would be a multiple of 4, while would be congruent to 2 modulo 4, as an odd square is congruent to 1 modulo 4).

From $a^2+b^2=c^2,$ assume is odd. We obtain $c^2-a^2=b^2$ and hence $(c-a)(c+a)=b^2.$ Then $\tfrac=\tfrac.$ Since $\tfrac$ is rational, we set it equal to $\tfrac$ in lowest terms. Thus $\tfrac=\tfrac,$ being the reciprocal of $\tfrac.$ Then solving

:$\frac+\frac=\frac, \quad \quad \frac-\frac=\frac$

for $\tfrac$ and $\tfrac$ gives

:$\frac=\frac\left(\frac+\frac\right)=\frac, \quad \quad \frac=\frac\left(\frac-\frac\right)=\frac.$

As $\tfrac$ is fully reduced, and are coprime, and they cannot both be even. If they were both odd, the numerator of $\tfrac$ would be a multiple of 4 (because an odd square is congruent to 1 modulo 4), and the denominator 2''mn'' would not be a multiple of 4. Since 4 would be the minimum possible even factor in the numerator and 2 would be the maximum possible even factor in the denominator, this would imply to be even despite defining it as odd. Thus one of and is odd and the other is even, and the numerators of the two fractions with denominator 2''mn'' are odd. Thus these fractions are fully reduced (an odd prime dividing this denominator divides one of and but not the other; thus it does not divide ). One may thus equate numerators with numerators and denominators with denominators, giving Euclid's formula
:$a = m^2 - n^2 ,\ \, b = 2mn ,\ \, c = m^2 + n^2$ with and coprime and of opposite parities.

A longer but more commonplace proof is given in Maor (2007) and Sierpiński (2003). Another proof is given in , as an instance of a general method that applies to every homogeneous Diophantine equation of degree two.

Interpretation of parameters in Euclid's formula

Suppose the sides of a Pythagorean triangle have lengths , , and , and suppose the angle between the leg of length and the hypotenuse of length is denoted as . Then $\tan=\tfrac$ and the full-angle trigonometric values are $\sin=\tfrac$, $\cos=\tfrac$, and .

A variant

The following variant of Euclid's formula is sometimes more convenient, as being more symmetric in and (same parity condition on and ).

If and are two odd integers such that , then
:$a = mn ,\quad b =\frac ,\quad c = \frac$
are three integers that form a Pythagorean triple, which is primitive if and only if and are coprime. Conversely, every primitive Pythagorean triple arises (after the exchange of and , if is even) from a unique pair of coprime odd integers.

Not exchanging ''a'' and ''b''

In the presentation above, it is said that all Pythagorean triples are uniquely obtained from Euclid's formula "after the exchange of ''a'' and ''b'', if ''a'' is even". Euclid's formula and the variant above can be merged as follows to avoid this exchange, leading to the following result.

Every primitive Pythagorean triple can be uniquely written
:$a = 2\varepsilon mn ,\quad b =\varepsilon (m^2 - n^2) ,\quad c = \varepsilon (m^2 + n^2),$
where and are positive coprime integers, and $\varepsilon=\frac12$ if and are both odd, and $\varepsilon=1$ otherwise. Equivalently, $\varepsilon=\frac12$ if is odd, and $\varepsilon=1$ if is even.

Elementary properties of primitive Pythagorean triples

General properties

The properties of a primitive Pythagorean triple with (without specifying which of or is even and which is odd) include:
* $\tfrac$ is always a perfect square. As it is only a necessary condition but not a sufficient one, it can be used in checking if a given triple of numbers is ''not'' a Pythagorean triple. For example, the triples and each pass the test that is a perfect square, but neither is a Pythagorean triple.
*When a triple of numbers , and forms a primitive Pythagorean triple, then and one-half of are both perfect squares; however this is not a sufficient condition, as the numbers pass the perfect squares test but are not a Pythagorean triple since .
*At most one of , , is a square.
*The area of a Pythagorean triangle cannot be the square or twice the square of an integer.
*Exactly one of , is divisible by 2 (is even), and the hypotenuse is always odd.
*Exactly one of , is divisible by 3, but never .
*Exactly one of , is divisible by 4, but never (because is never even).
*Exactly one of , , is divisible by 5.
*The largest number that always divides ''abc'' is 60.
*Any odd number of the form , where is an integer and , can be the odd leg of a primitive Pythagorean triple. See almost-isosceles primitive Pythagorean triples section below. However, only even numbers divisible by 4 can be the even leg of a primitive Pythagorean triple. This is because Euclid's formula for the even leg given above is and one of or must be even.
*The hypotenuse (which is always odd) is the sum of two squares. This requires all of its prime factors to be primes of the form . Therefore, c is of the form . A sequence of possible hypotenuse numbers for a primitive Pythagorean triple can be found at .
*The area is a congruent number divisible by 6.
*In every Pythagorean triangle, the radius of the incircle and the radii of the three excircles are positive integers. Specifically, for a primitive triple the radius of the incircle is , and the radii of the excircles opposite the sides , ''2mn'', and the hypotenuse are respectively , , and .
*As for any right triangle, the converse of Thales' theorem says that the diameter of the circumcircle equals the hypotenuse; hence for primitive triples the circumdiameter is , and the circumradius is half of this and thus is rational but non-integer (since and have opposite parity).
*When the area of a Pythagorean triangle is multiplied by the curvatures of its incircle and 3 excircles, the result is four positive integers , respectively. Integers satisfy Descartes's Circle Equation. Equivalently, the radius of the outer Soddy circle of any right triangle is equal to its semiperimeter. The outer Soddy center is located at , where is a rectangle, the right triangle and its hypotenuse.
*Only two sides of a primitive Pythagorean triple can be simultaneously prime because by Euclid's formula for generating a primitive Pythagorean triple, one of the legs must be composite and even. However, only one side can be an integer of perfect power $p \ge 2$ because if two sides were integers of perfect powers with equal exponent $p$ it would contradict the fact that there are no integer solutions to the Diophantine equation $x^ \pm y^=z^2$, with $x$, $y$ and $z$ being pairwise coprime.H. Darmon and L. Merel. Winding quotients and some variants of Fermat’s Last Theorem, J. Reine Angew. Math. 490 (1997), 81–100.
*There are no Pythagorean triangles in which the hypotenuse and one leg are the legs of another Pythagorean triangle; this is one of the equivalent forms of Fermat's right triangle theorem.
*Each primitive Pythagorean triangle has a ratio of area, , to squared semiperimeter, , that is unique to itself and is given by
:: $\frac = \frac = 1-\frac.$
*No primitive Pythagorean triangle has an integer altitude from the hypotenuse; that is, every primitive Pythagorean triangle is indecomposable.
*The set of all primitive Pythagorean triples forms a rooted ternary tree in a natural way; see Tree of primitive Pythagorean triples.
*Neither of the acute angles of a Pythagorean triangle can be a rational number of degrees. (This follows from Niven's theorem.)

Special cases

In addition, special Pythagorean triples with certain additional properties can be guaranteed to exist:
*Every integer greater than 2 that is not congruent to 2 mod 4 (in other words, every integer greater than 2 which is ''not'' of the form ) is part of a primitive Pythagorean triple. (If the integer has the form , one may take and in Euclid's formula; if the integer is , one may take and .)
*Every integer greater than 2 is part of a primitive or non-primitive Pythagorean triple. For example, the integers 6, 10, 14, and 18 are not part of primitive triples, but are part of the non-primitive triples , and .
*There exist infinitely many Pythagorean triples in which the hypotenuse and the longest leg differ by exactly one. Such triples are necessarily primitive and have the form . This results from Euclid's formula by remarking that the condition implies that the triple is primitive and must verify . This implies , and thus . The above form of the triples results thus of substituting for in Euclid's formula.
*There exist infinitely many primitive Pythagorean triples in which the hypotenuse and the longest leg differ by exactly two. They are all primitive, and are obtained by putting in Euclid's formula. More generally, for every integer , there exist infinitely many primitive Pythagorean triples in which the hypotenuse and the odd leg differ by . They are obtained by putting in Euclid's formula.
*There exist infinitely many Pythagorean triples in which the two legs differ by exactly one. For example, 20 + 21 = 29; these are generated by Euclid's formula when $\tfrac$ is a convergent to $\sqrt2.$
*For each positive integer , there exist Pythagorean triples with different hypotenuses and the same area.
*For each positive integer , there exist at least different primitive Pythagorean triples with the same leg , where is some positive integer (the length of the even leg is 2''mn'', and it suffices to choose with many factorizations, for example , where is a product of different odd primes; this produces at least different primitive triples).
*For each positive integer , there exist at least different Pythagorean triples with the same hypotenuse.
*If is a prime power, there exists a primitive Pythagorean triple if and only if the prime has the form ; this triple is unique up to the exchange of ''a'' and ''b''.
*More generally, a positive integer is the hypotenuse of a primitive Pythagorean triple if and only if each prime factor of is congruent to modulo ; that is, each prime factor has the form . In this case, the number of primitive Pythagorean triples with is , where is the number of distinct prime factors of .
*There exist infinitely many Pythagorean triples with square numbers for both the hypotenuse and the sum of the legs . According to Fermat, the smallest such triple has sides ; ; and . Here and . This is generated by Euclid's formula with parameter values and .
*There exist non-primitive Pythagorean triangles with integer altitude from the hypotenuse. Such Pythagorean triangles are known as decomposable since they can be split along this altitude into two separate and smaller Pythagorean triangles.

Geometry of Euclid's formula

Rational points on a unit circle

Euclid's formula for a Pythagorean triple

:$a = m^2-n^2,\quad b=2mn,\quad c=m^2+n^2$

can be understood in terms of the geometry of rational points on the unit circle .

In fact, a point in the Cartesian plane with coordinates belongs to the unit circle if . The point is ''rational'' if and are rational numbers, that is, if there are coprime integers such that
:$\biggl(\frac\biggr)^2\! + \biggl(\frac\biggr)^2=1.$

By multiplying both members by , one can see that the rational points on the circle are in one-to-one correspondence with the primitive Pythagorean triples.

The unit circle may also be defined by a parametric equation
:$x=\frac,\quad y=\frac.$
Euclid's formula for Pythagorean triples and the inverse relationship mean that, except for , a point on the circle is rational if and only if the corresponding value of is a rational number. Note that is also the tangent of half of the angle that is opposite the triangle side of length .

Stereographic approach

There is a correspondence between points on the unit circle with rational coordinates and primitive Pythagorean triples. At this point, Euclid's formulae can be derived either by methods of trigonometry or equivalently by using the stereographic projection.

For the stereographic approach, suppose that ′ is a point on the -axis with rational coordinates

:$P' = \left(\frac,0\right).$

Then, it can be shown by basic algebra that the point has coordinates

:$P = \left( \frac, \frac \right) = \left( \frac, \frac \right).$

This establishes that each rational point of the -axis goes over to a rational point of the unit circle. The converse, that every rational point of the unit circle comes from such a point of the -axis, follows by applying the inverse stereographic projection. Suppose that is a point of the unit circle with and rational numbers. Then the point ′ obtained by stereographic projection onto the -axis has coordinates

:$\left(\frac,0\right)$

which is rational.

In terms of algebraic geometry, the algebraic variety of rational points on the unit circle is birational to the affine line over the rational numbers. The unit circle is thus called a rational curve, and it is this fact which enables an explicit parameterization of the (rational number) points on it by means of rational functions.

Pythagorean triangles in a 2D lattice

A 2D lattice is a regular array of isolated points where if any one point is chosen as the Cartesian origin (0, 0), then all the other points are at where and range over all positive and negative integers. Any Pythagorean triangle with triple can be drawn within a 2D lattice with vertices at coordinates , and . The count of lattice points lying strictly within the bounds of the triangle is given by   $\tfrac;$ for primitive Pythagorean triples this interior lattice count is  $\tfrac.$ The area (by Pick's theorem equal to one less than the interior lattice count plus half the boundary lattice count) equals  $\tfrac$ .

The first occurrence of two primitive Pythagorean triples sharing the same area occurs with triangles with sides and common area 210 . The first occurrence of two primitive Pythagorean triples sharing the same interior lattice count occurs with and interior lattice count 2287674594 . Three primitive Pythagorean triples have been found sharing the same area: , , with area 13123110. As yet, no set of three primitive Pythagorean triples have been found sharing the same interior lattice count.

Enumeration of primitive Pythagorean triples

By Euclid's formula all primitive Pythagorean triples can be generated from integers $m$ and $n$ with $m>n>0$, $m+n$ odd and $\gcd(m, n)=1.$ Hence there is a 1 to 1 mapping of rationals (in lowest terms) to primitive Pythagorean triples where $\tfrac$ is in the interval $(0,1)$ and $m+n$ odd.

The reverse mapping from a primitive triple $(a , b , c)$ where $c>b>a>0$ to a rational $\tfrac$ is achieved by studying the two sums $a+c$ and $b+c.$ One of these sums will be a square that can be equated to $(m+n)^2$ and the other will be twice a square that can be equated to $2m^2.$ It is then possible to determine the rational $\tfrac.$

In order to enumerate primitive Pythagorean triples the rational can be expressed as an ordered pair $(n,m)$ and mapped to an integer using a pairing function such as Cantor's pairing function. An example can be seen at . It begins
::$8,18,19,32,33,34,\dots$ and gives rationals
::$\tfrac,\tfrac,\tfrac,\tfrac,\tfrac,\tfrac,\dots$ these, in turn, generate primitive triples
::$(3,4,5),(5,12,13),(8,15,17),(7,24,25),(20,21,29),(12,35,37),\dots$

Spinors and the modular group

Pythagorean triples can likewise be encoded into a square matrix of the form
:$X = \begin c+b & a\\ a & c-b \end.$
A matrix of this form is symmetric. Furthermore, the determinant of is
:$\det X = c^2 - a^2 - b^2\,$
which is zero precisely when is a Pythagorean triple. If corresponds to a Pythagorean triple, then as a matrix it must have rank 1.

Since is symmetric, it follows from a result in linear algebra that there is a column vector such that the outer product

holds, where the denotes the matrix transpose. Since ξ and -ξ produce the same Pythagorean triple, the vector ξ can be considered a spinor (for the Lorentz group SO(1, 2)). In abstract terms, the Euclid formula means that each primitive Pythagorean triple can be written as the outer product with itself of a spinor with integer entries, as in ().

The modular group Γ is the set of 2×2 matrices with integer entries

:$A = \begin\alpha&\beta\\ \gamma&\delta\end$

with determinant equal to one: . This set forms a group, since the inverse of a matrix in Γ is again in Γ, as is the product of two matrices in Γ. The modular group acts on the collection of all integer spinors. Furthermore, the group is transitive on the collection of integer spinors with relatively prime entries. For if has relatively prime entries, then

:$\beginm&-v\\n&u\end\begin1\\0\end = \beginm\\n\end$

where and are selected (by the Euclidean algorithm) so that .

By acting on the spinor ξ in (), the action of Γ goes over to an action on Pythagorean triples, provided one allows for triples with possibly negative components. Thus if is a matrix in , then

gives rise to an action on the matrix in (). This does not give a well-defined action on primitive triples, since it may take a primitive triple to an imprimitive one. It is convenient at this point (per ) to call a triple standard if and either are relatively prime or are relatively prime with odd. If the spinor has relatively prime entries, then the associated triple determined by () is a standard triple. It follows that the action of the modular group is transitive on the set of standard triples.

Alternatively, restrict attention to those values of and for which is odd and is even. Let the subgroup Γ(2) of Γ be the kernel of the group homomorphism

:$\Gamma=\mathrm(2,\mathbf)\to \mathrm(2,\mathbf_2)$

where is the special linear group over the finite field of integers modulo 2. Then Γ(2) is the group of unimodular transformations which preserve the parity of each entry. Thus if the first entry of ξ is odd and the second entry is even, then the same is true of for all . In fact, under the action (), the group Γ(2) acts transitively on the collection of primitive Pythagorean triples .

The group Γ(2) is the free group whose generators are the matrices
:$U=\begin1&2\\0&1\end,\qquad L=\begin1&0\\2&1\end.$
Consequently, every primitive Pythagorean triple can be obtained in a unique way as a product of copies of the matrices and .

Parent/child relationships

By a result of , all primitive Pythagorean triples can be generated from the (3, 4, 5) triangle by using the three linear transformations T₁, T₂, T₃ below, where , , are sides of a triple:

In other words, every primitive triple will be a "parent" to three additional primitive triples.
Starting from the initial node with , , and , the operation produces the new triple
:(3 − (2×4) + (2×5), (2×3) − 4 + (2×5), (2×3) − (2×4) + (3×5)) = (5, 12, 13),
and similarly and produce the triples (21, 20, 29) and (15, 8, 17).

The linear transformations T₁, T₂, and T₃ have a geometric interpretation in the language of quadratic forms. They are closely related to (but are not equal to) reflections generating the orthogonal group of over the integers.

Relation to Gaussian integers

Alternatively, Euclid's formulae can be analyzed and proved using the Gaussian integers. Gaussian integers are complex numbers of the form , where and are ordinary integers and is the square root of negative one. The units of Gaussian integers are ±1 and ±i. The ordinary integers are called the rational integers and denoted as ''. The Gaussian integers are denoted as . The right-hand side of the Pythagorean theorem may be factored in Gaussian integers:

:$c^2 = a^2+b^2 = (a+bi)\overline = (a+bi)(a-bi).$

A primitive Pythagorean triple is one in which and are coprime, i.e., they share no prime factors in the integers. For such a triple, either or is even, and the other is odd; from this, it follows that is also odd.

The two factors and of a primitive Pythagorean triple each equal the square of a Gaussian integer. This can be proved using the property that every Gaussian integer can be factored uniquely into Gaussian primes up to units. See also ''Werke'', 2:67–148. (This unique factorization follows from the fact that, roughly speaking, a version of the Euclidean algorithm can be defined on them.) The proof has three steps. First, if and share no prime factors in the integers, then they also share no prime factors in the Gaussian integers. (Assume and with Gaussian integers , and and not a unit. Then and lie on the same line through the origin. All Gaussian integers on such a line are integer multiples of some Gaussian integer . But then the integer ''gh'' ≠ ±1 divides both and .) Second, it follows that and likewise share no prime factors in the Gaussian integers. For if they did, then their common divisor would also divide and . Since and are coprime, that implies that divides . From the formula , that in turn would imply that is even, contrary to the hypothesis of a primitive Pythagorean triple. Third, since is a square, every Gaussian prime in its factorization is doubled, i.e., appears an even number of times. Since and share no prime factors, this doubling is also true for them. Hence, and are squares.

Thus, the first factor can be written

:$a+bi = \varepsilon\left(m + ni \right)^2, \quad \varepsilon\in\.$

The real and imaginary parts of this equation give the two formulas:

:$\begin\varepsilon = +1, & \quad a = +\left( m^2 - n^2 \right),\quad b = +2mn; \\ \varepsilon = -1, & \quad a = -\left( m^2 - n^2 \right),\quad b = -2mn; \\ \varepsilon = +i, & \quad a = -2mn,\quad b = +\left( m^2 - n^2 \right); \\ \varepsilon = -i, & \quad a = +2mn,\quad b = -\left( m^2 - n^2 \right).\end$

For any primitive Pythagorean triple, there must be integers and such that these two equations are satisfied. Hence, every Pythagorean triple can be generated from some choice of these integers.

As perfect square Gaussian integers

If we consider the square of a Gaussian integer we get the following direct interpretation of Euclid's formula as representing the perfect square of a Gaussian integer.

:$(m+ni)^2 = (m^2-n^2)+2mni.$

Using the facts that the Gaussian integers are a Euclidean domain and that for a Gaussian integer p $, p, ^2$ is always a square it is possible to show that a Pythagorean triple corresponds to the square of a prime Gaussian integer if the hypotenuse is prime.

If the Gaussian integer is not prime then it is the product of two Gaussian integers p and q with $, p, ^2$ and $, q, ^2$ integers. Since magnitudes multiply in the Gaussian integers, the product must be $, p, , q,$, which when squared to find a Pythagorean triple must be composite. The contrapositive completes the proof.

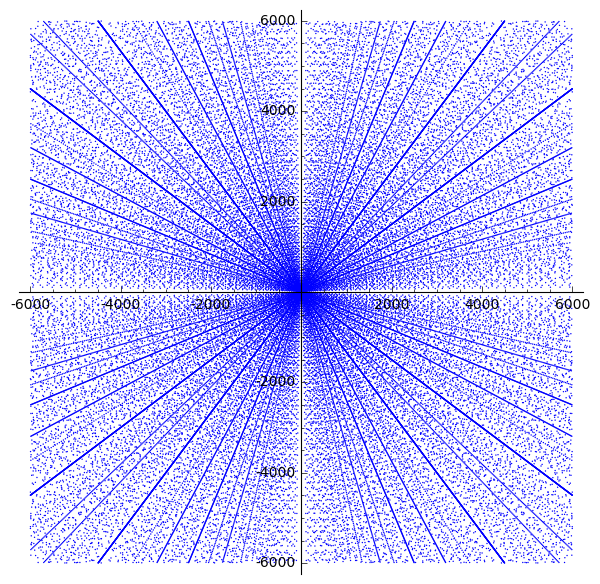
Distribution of triples

There are a number of results on the distribution of Pythagorean triples. In the scatter plot, a number of obvious patterns are already apparent. Whenever the legs of a primitive triple appear in the plot, all integer multiples of must also appear in the plot, and this property produces the appearance of lines radiating from the origin in the diagram.

Within the scatter, there are sets of parabolic patterns with a high density of points and all their foci at the origin, opening up in all four directions. Different parabolas intersect at the axes and appear to reflect off the axis with an incidence angle of 45 degrees, with a third parabola entering in a perpendicular fashion. Within this quadrant, each arc centered on the origin shows that section of the parabola that lies between its tip and its intersection with its semi-latus rectum.

These patterns can be explained as follows. If $a^2/4n$ is an integer, then (, $, n-a^2/4n,$, $n+a^2/4n$) is a Pythagorean triple. (In fact every Pythagorean triple can be written in this way with integer , possibly after exchanging and , since $n=(b+c)/2$ and and cannot both be odd.) The Pythagorean triples thus lie on curves given by $b = , n-a^2/4n,$, that is, parabolas reflected at the -axis, and the corresponding curves with and interchanged. If is varied for a given (i.e. on a given parabola), integer values of occur relatively frequently if is a square or a small multiple of a square. If several such values happen to lie close together, the corresponding parabolas approximately coincide, and the triples cluster in a narrow parabolic strip. For instance, , ,
, and ; the corresponding parabolic strip around is clearly visible in the scatter plot.

The angular properties described above follow immediately from the functional form of the parabolas. The parabolas are reflected at the -axis at , and the derivative of with respect to at this point is –1; hence the incidence angle is 45°. Since the clusters, like all triples, are repeated at integer multiples, the value also corresponds to a cluster. The corresponding parabola intersects the -axis at right angles at , and hence its reflection upon interchange of and intersects the -axis at right angles at , precisely where the parabola for is reflected at the -axis. (The same is of course true for and interchanged.)

Albert Fässler and others provide insights into the significance of these parabolas in the context of conformal mappings.

Special cases and related equations

The Platonic sequence

The case of the more general construction of Pythagorean triples has been known for a long time. Proclus, in his commentary to the 47th Proposition of the first book of Euclid's ''Elements'', describes it as follows:

Certain methods for the discovery of triangles of this kind are handed down, one which they refer to Plato, and another to Pythagoras. (The latter) starts from odd numbers. For it makes the odd number the smaller of the sides about the right angle; then it takes the square of it, subtracts unity and makes half the difference the greater of the sides about the right angle; lastly it adds unity to this and so forms the remaining side, the hypotenuse.

...For the method of Plato argues from even numbers. It takes the given even number and makes it one of the sides about the right angle; then, bisecting this number and squaring the half, it adds unity to the square to form the hypotenuse, and subtracts unity from the square to form the other side about the right angle. ... Thus it has formed the same triangle that which was obtained by the other method.

In equation form, this becomes:

is odd (Pythagoras, c. 540 BC):

:$\texta : \textb = : \textc = .$

is even (Plato, c. 380 BC):

:$\texta : \textb = \left(\right)^2 - 1 : \textc = \left(\right)^2 + 1$

It can be shown that all Pythagorean triples can be obtained, with appropriate rescaling, from the basic Platonic sequence (, and ) by allowing to take non-integer rational values. If is replaced with the fraction in the sequence, the result is equal to the 'standard' triple generator (2''mn'', ,) after rescaling. It follows that every triple has a corresponding rational value which can be used to generate a similar triangle (one with the same three angles and with sides in the same proportions as the original). For example, the Platonic equivalent of is generated by as . The Platonic sequence itself can be derived by following the steps for 'splitting the square' described in Diophantus II.VIII.

The Jacobi–Madden equation

The equation,

:$a^4+b^4+c^4+d^4 = (a+b+c+d)^4$

is equivalent to the special Pythagorean triple,

:$(a^2+ab+b^2)^2+(c^2+cd+d^2)^2 = ((a+b)^2+(a+b)(c+d)+(c+d)^2)^2$

There is an infinite number of solutions to this equation as solving for the variables involves an elliptic curve. Small ones are,

:$a, b, c, d = -2634, 955, 1770, 5400$

:$a, b, c, d = -31764, 7590, 27385, 48150$

Equal sums of two squares

One way to generate solutions to $a^2+b^2=c^2+d^2$ is to parametrize ''a, b, c, d'' in terms of integers ''m, n, p, q'' as follows:

:$(m^2+n^2)(p^2+q^2)=(mp-nq)^2+(np+mq)^2=(mp+nq)^2+(np-mq)^2.$

Equal sums of two fourth powers

Given two sets of Pythagorean triples,

:$(a^2-b^2)^2+(2a b)^2 = (a^2+b^2)^2$

:$(c^2-d^2)^2+(2c d)^2 = (c^2+d^2)^2$

the problem of finding equal products of a non-hypotenuse side and the hypotenuse,

:$(a^2 -b^2)(a^2+b^2) = (c^2 -d^2)(c^2+d^2)$

is easily seen to be equivalent to the equation,

:$a^4 -b^4 = c^4 -d^4$

and was first solved by Euler as $a, b, c, d = 133,59,158,134.$ Since he showed this is a rational point in an elliptic curve, then there is an infinite number of solutions. In fact, he also found a 7th degree polynomial parameterization.

Descartes' Circle Theorem

For the case of Descartes' circle theorem where all variables are squares,

:$2(a^4+b^4+c^4+d^4) = (a^2+b^2+c^2+d^2)^2$

Euler showed this is equivalent to three simultaneous Pythagorean triples,

:$(2ab)^2+(2cd)^2 = (a^2+b^2-c^2-d^2)^2$

:$(2ac)^2+(2bd)^2 = (a^2-b^2+c^2-d^2)^2$

:$(2ad)^2+(2bc)^2 = (a^2-b^2-c^2+d^2)^2$

There is also an infinite number of solutions, and for the special case when $a+b=c$, then the equation simplifies to,

:$4(a^2+a b+b^2) = d^2$

with small solutions as $a, b, c, d = 3, 5, 8, 14$ and can be solved as binary quadratic forms.

Almost-isosceles Pythagorean triples

No Pythagorean triples are isosceles, because the ratio of the hypotenuse to either other side is , but cannot be expressed as the ratio of 2 integers.

There are, however, right-angled triangles with integral sides for which the lengths of the non-hypotenuse sides differ by one, such as,

:$3^2+4^2 = 5^2$

:$20^2+21^2 = 29^2$

and an infinite number of others. They can be completely parameterized as,

:$\left(\tfrac\right)^2+\left(\tfrac\right)^2 = y^2$

where are the solutions to the Pell equation $x^2-2y^2 = -1.$

If , , are the sides of this type of primitive Pythagorean triple then the solution to the Pell equation is given by the recursive formula

:$a_n=6a_-a_+2$ with $a_1=3$ and $a_2=20$
:$b_n=6b_-b_-2$ with $b_1=4$ and $b_2=21$
:$c_n=6c_-c_$ with $c_1=5$ and .

This sequence of primitive Pythagorean triples forms the central stem (trunk) of the rooted ternary tree of primitive Pythagorean triples.

When it is the longer non-hypotenuse side and hypotenuse that differ by one, such as in

:$5^2+12^2 = 13^2$

:$7^2+24^2 = 25^2$

then the complete solution for the primitive Pythagorean triple , , is

:$a=2m+1, \quad b=2m^2+2m, \quad c=2m^2+2m+1$

and

:$(2m+1)^2+(2m^2+2m)^2=(2m^2+2m+1)^2$

where integer $m>0$ is the generating parameter.

It shows that all odd numbers (greater than 1) appear in this type of almost-isosceles primitive Pythagorean triple. This sequence of primitive Pythagorean triples forms the right hand side outer stem of the rooted ternary tree of primitive Pythagorean triples.

Another property of this type of almost-isosceles primitive Pythagorean triple is that the sides are related such that
:$a^b+b^a=Kc$
for some integer $K$. Or in other words $a^b+b^a$ is divisible by $c$ such as in
:$(5^+12^5)/13 = 18799189$.

Fibonacci numbers in Pythagorean triples

Starting with 5, every second Fibonacci number is the length of the hypotenuse of a right triangle with integer sides, or in other words, the largest number in a Pythagorean triple, obtained from the formula
$(F_nF_)^2 + (2F_F_)^2 = F_^2.$
The sequence of Pythagorean triangles obtained from this formula has sides of lengths
:(3,4,5), (5,12,13), (16,30,34), (39,80,89), ...
The middle side of each of these triangles is the sum of the three sides of the preceding triangle.

Generalizations

There are several ways to generalize the concept of Pythagorean triples.

Pythagorean -tuple

The expression
:$\left(m_1^2 - m_2^2 - \ldots - m_n^2\right)^2 + \sum_^n (2 m_1 m_k)^2 = \left(m_1^2 + \ldots + m_n^2\right)^2$
is a Pythagorean -tuple for any tuple of positive integers with . The Pythagorean -tuple can be made primitive by dividing out by the largest common divisor of its values.

Furthermore, any primitive Pythagorean -tuple can be found by this approach. Use to get a Pythagorean -tuple by the above formula and divide out by the largest common integer divisor, which is . Dividing out by the largest common divisor of these values gives the same primitive Pythagorean -tuple; and there is a one-to-one correspondence between tuples of setwise coprime positive integers satisfying and primitive Pythagorean -tuples.

Examples of the relationship between setwise coprime values $\vec$ and primitive Pythagorean -tuples include:

:$\begin \vec = (1) & \leftrightarrow 1^2 = 1^2 \\ \vec = (2, 1) & \leftrightarrow 3^2 + 4^2 = 5^2 \\ \vec = (2, 1, 1) & \leftrightarrow 1^2 + 2^2 + 2^2 = 3^2 \\ \vec = (3, 1, 1, 1) & \leftrightarrow 1^2 + 1^2 + 1^2 + 1^2 = 2^2 \\ \vec = (5, 1, 1, 2, 3) & \leftrightarrow 1^2 + 1^2 + 1^2 + 2^2 + 3^2 = 4^2 \\ \vec = (4, 1, 1, 1, 1, 2) & \leftrightarrow 1^2 + 1^2 + 1^2 + 1^2 + 1^2 + 2^2 = 3^2 \\ \vec = (5, 1, 1, 1, 2, 2, 2) & \leftrightarrow 1^2 + 1^2 + 1^2 + 1^2 + 2^2 + 2^2 + 2^2 = 4^2 \end$

Consecutive squares

Since the sum of consecutive squares beginning with is given by the formula,

:$F(k,m)=km(k-1+m)+\frac$

one may find values so that is a square, such as one by Hirschhorn where the number of terms is itself a square,

:$m=\tfrac,\; k=v^2,\; F(m,k)=\tfrac$

and is any integer not divisible by 2 or 3. For the smallest case , hence , this yields the well-known cannonball-stacking problem of Lucas,

:$0^2+1^2+2^2+\dots+24^2 = 70^2$

a fact which is connected to the Leech lattice.

In addition, if in a Pythagorean -tuple () all addends are consecutive except one, one can use the equation,

:$F(k,m) + p^ = (p+1)^$

Since the second power of cancels out, this is only linear and easily solved for as $p=\tfrac$ though , should be chosen so that is an integer, with a small example being , yielding,

:$1^2+2^2+3^2+4^2+5^2+27^2=28^2$

Thus, one way of generating Pythagorean -tuples is by using, for various ,

:$x^2+(x+1)^2+\cdots +(x+q)^2+p^2=(p+1)^2,$

where ''q = n''–2 and where

:$p=\frac.$

Fermat's Last Theorem

A generalization of the concept of Pythagorean triples is the search for triples of positive integers , , and , such that , for some strictly greater than 2. Pierre de Fermat in 1637 claimed that no such triple exists, a claim that came to be known as Fermat's Last Theorem because it took longer than any other conjecture by Fermat to be proved or disproved. The first proof was given by Andrew Wiles in 1994.

or th powers summing to an th power

Another generalization is searching for sequences of positive integers for which the th power of the last is the sum of the th powers of the previous terms. The smallest sequences for known values of are:

* = 3: .
* = 4:
* = 5:
* = 7:
* = 8:

For the case, in which $x^3+y^3+z^3=w^3,$ called the Fermat cubic, a general formula exists giving all solutions.

A slightly different generalization allows the sum of th powers to equal the sum of th powers. For example:
* (): 1 + 12 = 9 + 10, made famous by Hardy's recollection of a conversation with Ramanujan about the number 1729 being the smallest number that can be expressed as a sum of two cubes in two distinct ways.

There can also exist positive integers whose th powers sum to an th power (though, by Fermat's Last Theorem, not for ; these are counterexamples to Euler's sum of powers conjecture. The smallest known counterexamples are

* : (95800, 217519, 414560; 422481)
* : (27, 84, 110, 133; 144)

Heronian triangle triples

A Heronian triangle is commonly defined as one with integer sides whose area is also an integer. The lengths of the sides of such a triangle form a Heronian triple for .
Every Pythagorean triple is a Heronian triple, because at least one of the legs , must be even in a Pythagorean triple, so the area ''ab''/2 is an integer. Not every Heronian triple is a Pythagorean triple, however, as the example with area 24 shows.

If is a Heronian triple, so is where is any positive integer; its area will be the integer that is times the integer area of the triangle.
The Heronian triple is primitive provided ''a'', ''b'', ''c'' are setwise coprime. (With primitive Pythagorean triples the stronger statement that they are ''pairwise'' coprime also applies, but with primitive Heronian triangles the stronger statement does not always hold true, such as with .) Here are a few of the simplest primitive Heronian triples that are not Pythagorean triples:

: (4, 13, 15) with area 24
: (3, 25, 26) with area 36
: (7, 15, 20) with area 42
: (6, 25, 29) with area 60
: (11, 13, 20) with area 66
: (13, 14, 15) with area 84
: (13, 20, 21) with area 126

By Heron's formula, the extra condition for a triple of positive integers with to be Heronian is that

:
or equivalently
:

be a nonzero perfect square divisible by 16.

Application to cryptography

Primitive Pythagorean triples have been used in cryptography as random sequences and for the generation of keys. Kak, S. and Prabhu, M. Cryptographic applications of primitive Pythagorean triples. Cryptologia, 38:215–222, 2014

/ref>

See also

* Boolean Pythagorean triples problem
* Brahmagupta triangle
* Congruum
* Diophantus II.VIII
* Eisenstein triple
* Euler brick
* Heronian triangle
* Hilbert's theorem 90
* Integer triangle
* Modular arithmetic
* Nonhypotenuse number
* Plimpton 322
* Pythagorean prime
* Pythagorean quadruple
* Quadric
* Tangent half-angle formula
* Trigonometric identity

Notes

References

*
*
*
*
*
*
*
*
*
*
*
*

External links

Clifford Algebras and Euclid's Parameterization of Pythagorean triples

Curious Consequences of a Miscopied Quadratic


* ttps://web.archive.org/web/20160304023524/http://people.wcsu.edu/sandifere/Academics/2007Spring/Mat342/PythagTrip02.pdf Generating Pythagorean Triples Using Arithmetic Progressions*

Interactive Calculator for Pythagorean Triples



Parameterization of Pythagorean Triples by a single triple of polynomials
*

Pythagorean Triples and the Unit Circle
chap. 2–3, in

by Joseph H. Silverman, 3rd ed., 2006, Pearson Prentice Hall, Upper Saddle River, NJ,

Pythagorean Triples
at cut-the-knot Interactive Applet showing unit circle relationships to Pythagorean Triples

Pythagorean Triplets

The Remarkable Incircle of a Triangle

Solutions to Quadratic Compatible Pairs in relation to Pythagorean Triples


* ttp://www.cut-the-knot.org/pythagoras/PT_matrix.shtml The Trinary Tree(s) underlying Primitive Pythagorean Triplesat cut-the-knot
*

{{DEFAULTSORT:Pythagorean Triple
Arithmetic problems of plane geometry
Diophantine equations
Triple
Squares in number theory