|
Brahmagupta Triangle
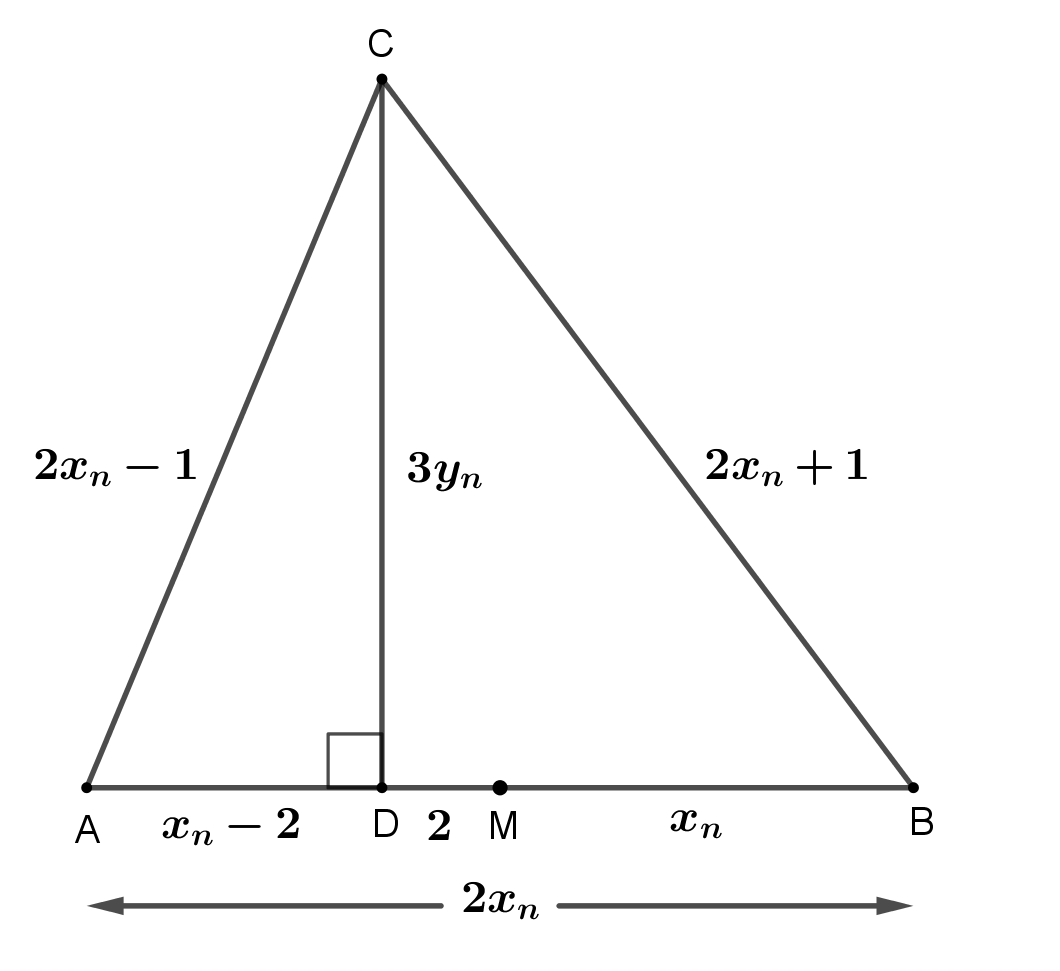
A Brahmagupta triangle is a triangle whose side lengths are consecutive positive integers and area is a positive integer. The triangle whose side lengths are 3, 4, 5 is a Brahmagupta triangle and so also is the triangle whose side lengths are 13, 14, 15. The Brahmagupta triangle is a special case of the Heronian triangle which is a triangle whose side lengths and area are all positive integers but the side lengths need not necessarily be consecutive integers. A Brahmagupta triangle is called as such in honor of the Indian astronomer and mathematician Brahmagupta (c. 598 – c. 668 CE) who gave a list of the first eight such triangles without explaining the method by which he computed that list. A Brahmagupta triangle is also called a Fleenor-Heronian triangle in honor of Charles R. Fleenor who discussed the concept in a paper published in 1996. Some of the other names by which Brahmagupta triangles are known are super-Heronian triangle and almost-equilateral Heronian triangle. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimensional line segments. A triangle has three internal angles, each one bounded by a pair of adjacent edges; the sum of angles of a triangle always equals a straight angle (180 degrees or π radians). The triangle is a plane figure and its interior is a planar region. Sometimes an arbitrary edge is chosen to be the ''base'', in which case the opposite vertex is called the ''apex''; the shortest segment between the base and apex is the ''height''. The area of a triangle equals one-half the product of height and base length. In Euclidean geometry, any two points determine a unique line segment situated within a unique straight line, and any three points that do not all lie on the same straight line determine a unique triangle situated w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |