Elliptical orbit

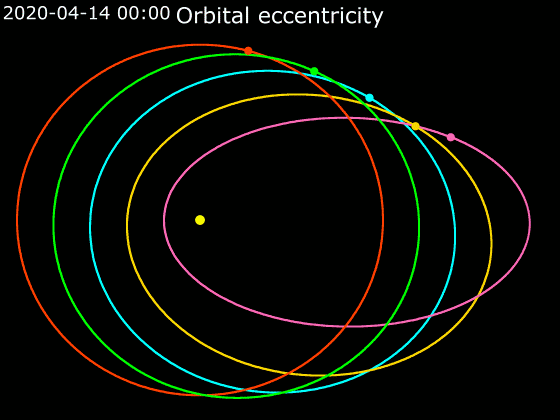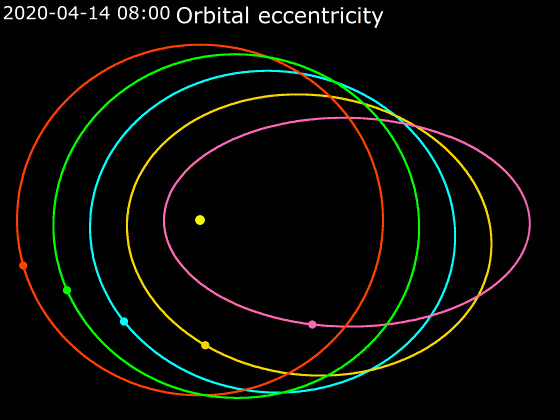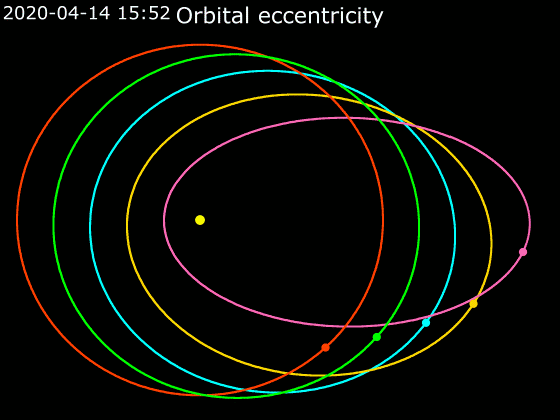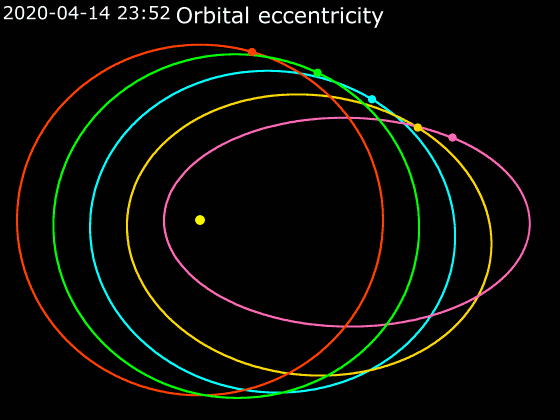In astrodynamics or celestial mechanics, an elliptical orbit or eccentric orbit is an orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. Some orbits have been referred to as "elongated orbits" if the eccentricity is "high" but that is not an explanatory term. For the simple two body problem, all orbits are ellipses.

In a gravitational two-body problem, both bodies follow similar elliptical orbits with the same orbital period around their common barycenter. The relative position of one body with respect to the other also follows an elliptic orbit.

Examples of elliptic orbits include Hohmann transfer orbits, Molniya orbits, and tundra orbits.

Velocity

Under standard assumptions, no other forces acting except two spherically symmetrical bodies $(m_1)$ and $(m_2)$, the orbital speed ($v\,$) of one body traveling along an elliptical orbit can be computed from the vis-viva equation as:
:$v = \sqrt$
where:
*$\mu\,$ is the standard gravitational parameter, $G(m_1+m_2)$, often expressed as $GM$ when one body is much larger than the other.
*$r\,$ is the distance between the orbiting body and center of mass.
*$a\,\!$ is the length of the semi-major axis.

The velocity equation for a hyperbolic trajectory has either $(+)$, or it is the same with the convention that in that case $(a)$ is negative.

Orbital period

Under standard assumptions the orbital period ($T\,\!$) of a body travelling along an elliptic orbit can be computed as:
:$T=2\pi\sqrt$
where:
*$\mu$ is the standard gravitational parameter.
*$a\,\!$ is the length of the semi-major axis.
Conclusions:
*The orbital period is equal to that for a circular orbit with the orbital radius equal to the semi-major axis ($a\,\!$),
*For a given semi-major axis the orbital period does not depend on the eccentricity (See also: Kepler's third law).

Energy

Under standard assumptions, the specific orbital energy ($\epsilon$) of an elliptic orbit is negative and the orbital energy conservation equation (the Vis-viva equation) for this orbit can take the form:
:$-=-=\epsilon<0$
where:
*$v\,$ is the orbital speed of the orbiting body,
*$r\,$ is the distance of the orbiting body from the central body,
*$a\,$ is the length of the semi-major axis,
*$\mu\,$ is the standard gravitational parameter.
Conclusions:
*For a given semi-major axis the specific orbital energy is independent of the eccentricity.

Using the virial theorem to find:
*the time-average of the specific potential energy is equal to −2ε
**the time-average of ''r''⁻¹ is ''a''⁻¹
*the time-average of the specific kinetic energy is equal to ε

Energy in terms of semi major axis

It can be helpful to know the energy in terms of the semi major axis (and the involved masses). The total energy of the orbit is given by
:$E = - G \frac$,

where a is the semi major axis.

Derivation

Since gravity is a central force, the angular momentum is constant:
:$\dot = \mathbf \times \mathbf = \mathbf \times F(r)\mathbf = 0$

At the closest and furthest approaches, the angular momentum is perpendicular to the distance from the mass orbited, therefore:
:$L = r p = r m v$.

The total energy of the orbit is given by
:$E = \fracm v^2 - G \frac$.

Substituting for v, the equation becomes
:$E = \frac\frac - G \frac$.

This is true for r being the closest / furthest distance so two simultaneous equations are made, which when solved for E:
:$E = - G \frac$

Since $r_1 = a + a \epsilon$ and $r_2 = a - a \epsilon$, where epsilon is the eccentricity of the orbit, the stated result is reached.

Flight path angle

The flight path angle is the angle between the orbiting body's velocity vector (equal to the vector tangent to the instantaneous orbit) and the local horizontal. Under standard assumptions of the conservation of angular momentum the flight path angle $\phi$ satisfies the equation:
:$h\, = r\, v\, \cos \phi$
where:
* $h\,$ is the specific relative angular momentum of the orbit,
* $v\,$ is the orbital speed of the orbiting body,
* $r\,$ is the radial distance of the orbiting body from the central body,
* $\phi \,$ is the flight path angle

$\psi$ is the angle between the orbital velocity vector and the semi-major axis. $\nu$ is the local true anomaly. $\phi = \nu + \frac - \psi$, therefore,
:$\cos \phi = \sin(\psi - \nu) = \sin\psi\cos\nu - \cos\psi\sin\nu = \frac$
:$\tan \phi = \frac$

where $e$ is the eccentricity.

The angular momentum is related to the vector cross product of position and velocity, which is proportional to the sine of the angle between these two vectors. Here $\phi$ is defined as the angle which differs by 90 degrees from this, so the cosine appears in place of the sine.

Equation of motion

From initial position and velocity

An orbit equation defines the path of an orbiting body $m_2\,\!$ around central body $m_1\,\!$ relative to $m_1\,\!$, without specifying position as a function of time. If the eccentricity is less than 1 then the equation of motion describes an elliptical orbit. Because Kepler's equation $M = E - e \sin E$ has no general closed-form solution for the Eccentric anomaly (E) in terms of the Mean anomaly (M), equations of motion as a function of time also have no closed-form solution (although numerical solutions exist for both).

However, closed-form time-independent path equations of an elliptic orbit with respect to a central body can be determined from just an initial position ($\mathbf$) and velocity ($\mathbf$).

For this case it is convenient to use the following assumptions which differ somewhat from the standard assumptions above:

:# The central body's position is at the origin and is the primary focus ($\mathbf$) of the ellipse (alternatively, the center of mass may be used instead if the orbiting body has a significant mass)
:# The central body's mass (m1) is known
:# The orbiting body's initial position($\mathbf$) and velocity($\mathbf$) are known
:# The ellipse lies within the XY-plane

The fourth assumption can be made without loss of generality because any three points (or vectors) must lie within a common plane. Under these assumptions the second focus (sometimes called the "empty" focus) must also lie within the XY-plane: $\mathbf = \left(f_x,f_y\right)$ .

Using vectors

The general equation of an ellipse under these assumptions using vectors is:

:$, \mathbf - \mathbf, + , \mathbf, = 2a \qquad\mid z=0$

where:
*$a\,\!$ is the length of the semi-major axis.
*$\mathbf = \left(f_x,f_y\right)$ is the second ("empty") focus.
*$\mathbf = \left(x,y\right)$ is any (x,y) value satisfying the equation.

The semi-major axis length (a) can be calculated as:

:$a = \frac$

where $\mu\ = Gm_1$ is the standard gravitational parameter.

The empty focus ($\mathbf = \left(f_x,f_y\right)$) can be found by first determining the Eccentricity vector:

:$\mathbf = \frac - \frac$

Where $\mathbf$ is the specific angular momentum of the orbiting body:

:$\mathbf = \mathbf \times \mathbf$

Then

:$\mathbf = -2a\mathbf$

Using XY Coordinates

This can be done in cartesian coordinates using the following procedure:

The general equation of an ellipse under the assumptions above is:

:$\sqrt + \sqrt = 2a \qquad\mid z=0$

Given:
:$r_x, r_y \quad$ the initial position coordinates
:$v_x, v_y \quad$ the initial velocity coordinates

and
:$\mu = Gm_1 \quad$ the gravitational parameter

Then:
:$h = r_x v_y - r_y v_x \quad$ specific angular momentum

:$r = \sqrt \quad$ initial distance from F1 (at the origin)

:$a = \frac \quad$ the semi-major axis length

:$e_x = \frac - \frac \quad$ the Eccentricity vector coordinates
:$e_y = \frac + \frac \quad$

Finally, the empty focus coordinates
:$f_x = - 2 a e_x \quad$
:$f_y = - 2 a e_y \quad$

Now the result values ''fx, fy'' and ''a'' can be applied to the general ellipse equation above.

Orbital parameters

The state of an orbiting body at any given time is defined by the orbiting body's position and velocity with respect to the central body, which can be represented by the three-dimensional Cartesian coordinates (position of the orbiting body represented by x, y, and z) and the similar Cartesian components of the orbiting body's velocity. This set of six variables, together with time, are called the orbital state vectors. Given the masses of the two bodies they determine the full orbit. The two most general cases with these 6 degrees of freedom are the elliptic and the hyperbolic orbit. Special cases with fewer degrees of freedom are the circular and parabolic orbit.

Because at least six variables are absolutely required to completely represent an elliptic orbit with this set of parameters, then six variables are required to represent an orbit with any set of parameters. Another set of six parameters that are commonly used are the orbital elements.

Solar System

In the Solar System, planets, asteroids, most comets, and some pieces of space debris have approximately elliptical orbits around the Sun. Strictly speaking, both bodies revolve around the same focus of the ellipse, the one closer to the more massive body, but when one body is significantly more massive, such as the sun in relation to the earth, the focus may be contained within the larger massing body, and thus the smaller is said to revolve around it. The following chart of the perihelion and aphelion of the planets, dwarf planets, and Halley's Comet demonstrates the variation of the eccentricity of their elliptical orbits. For similar distances from the sun, wider bars denote greater eccentricity. Note the almost-zero eccentricity of Earth and Venus compared to the enormous eccentricity of Halley's Comet and Eris.

Radial elliptic trajectory

A radial trajectory can be a double line segment, which is a degenerate ellipse with semi-minor axis = 0 and eccentricity = 1. Although the eccentricity is 1, this is not a parabolic orbit. Most properties and formulas of elliptic orbits apply. However, the orbit cannot be closed. It is an open orbit corresponding to the part of the degenerate ellipse from the moment the bodies touch each other and move away from each other until they touch each other again. In the case of point masses one full orbit is possible, starting and ending with a singularity. The velocities at the start and end are infinite in opposite directions and the potential energy is equal to minus infinity.

The radial elliptic trajectory is the solution of a two-body problem with at some instant zero speed, as in the case of dropping an object (neglecting air resistance).

History

The Babylonians were the first to realize that the Sun's motion along the ecliptic was not uniform, though they were unaware of why this was; it is today known that this is due to the Earth moving in an elliptic orbit around the Sun, with the Earth moving faster when it is nearer to the Sun at perihelion and moving slower when it is farther away at aphelion.

In the 17th century, Johannes Kepler discovered that the orbits along which the planets travel around the Sun are ellipses with the Sun at one focus, and described this in his first law of planetary motion. Later, Isaac Newton explained this as a corollary of his law of universal gravitation.

See also

* Apsis
* Characteristic energy
* Ellipse
* List of orbits
* Orbital eccentricity
* Orbit equation
* Parabolic trajectory

References

Sources

*
*
*

External links

Java applet animating the orbit of a satellite
in an elliptic Kepler orbit around the Earth with any value for semi-major axis and eccentricity.


Lunar photographic comparison


Solar photographic comparison
* http://www.castor2.ca

{{Portal bar, Astronomy, Stars, Spaceflight, Outer space, Solar System
Orbits