Coordination Number on:
[Wikipedia]
[Google]
[Amazon]
In

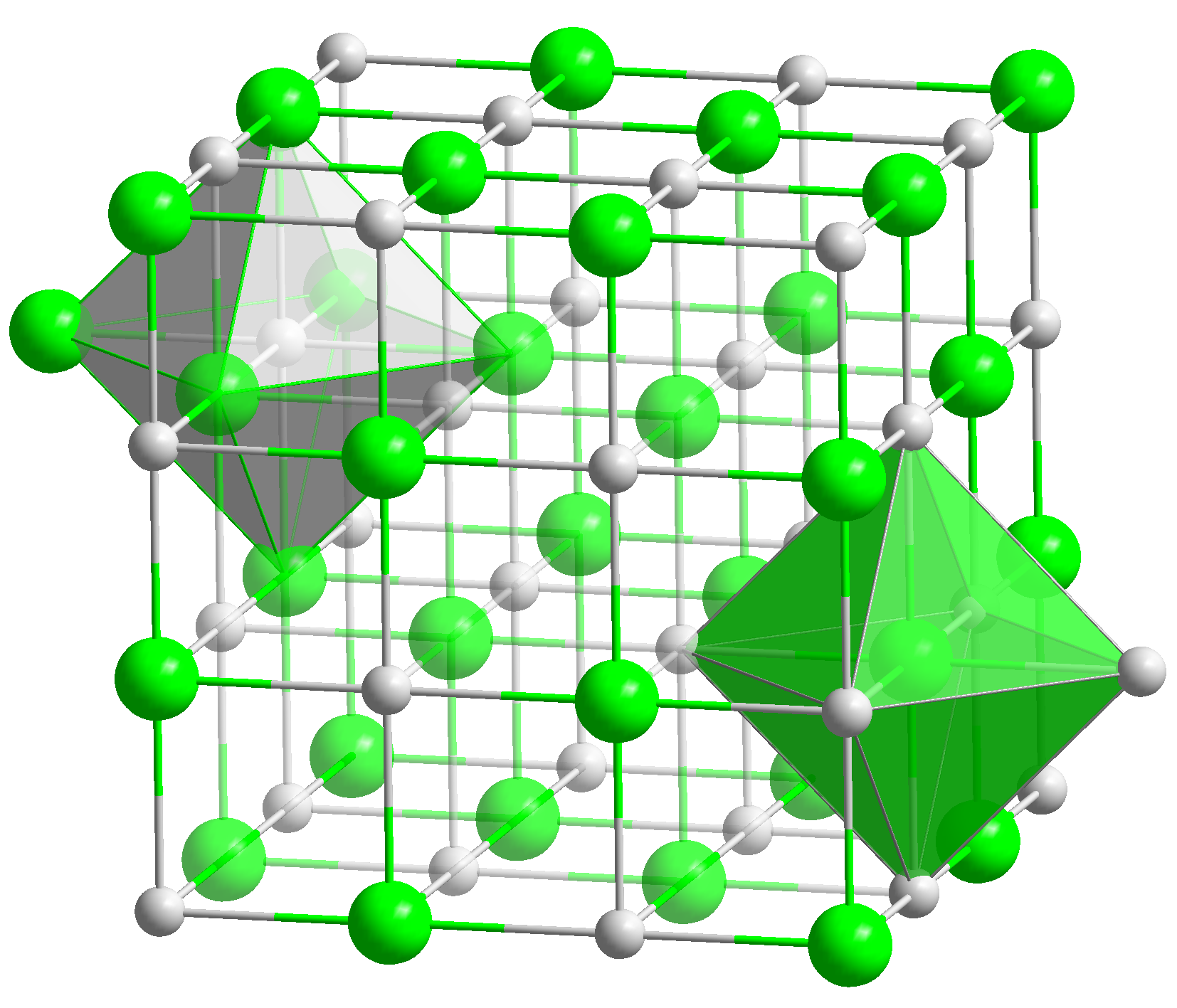 For chemical compounds with regular lattices such as
For chemical compounds with regular lattices such as
 In Nickel arsenide (NiAs) and several related compounds, the coordination number of the metal is ambiguous. The metal is bound to six As ligands, but also has two Ni---Ni contacts that could qualify as bonds.
In Nickel arsenide (NiAs) and several related compounds, the coordination number of the metal is ambiguous. The metal is bound to six As ligands, but also has two Ni---Ni contacts that could qualify as bonds. Two other examples of commonly-encountered chemicals are Fe2O3 and TiO2. Fe2O3 has a crystal structure that can be described as having a near close packed array of oxygen atoms with iron atoms filling two thirds of the octahedral holes. However each iron atom has 3 nearest neighbors and 3 others a little further away. The structure is quite complex, the oxygen atoms are coordinated to four iron atoms and the iron atoms in turn share vertices, edges and faces of the distorted octahedra. TiO2 has the
Two other examples of commonly-encountered chemicals are Fe2O3 and TiO2. Fe2O3 has a crystal structure that can be described as having a near close packed array of oxygen atoms with iron atoms filling two thirds of the octahedral holes. However each iron atom has 3 nearest neighbors and 3 others a little further away. The structure is quite complex, the oxygen atoms are coordinated to four iron atoms and the iron atoms in turn share vertices, edges and faces of the distorted octahedra. TiO2 has the
chemistry
Chemistry is the scientific study of the properties and behavior of matter. It is a physical science within the natural sciences that studies the chemical elements that make up matter and chemical compound, compounds made of atoms, molecules a ...
, crystallography
Crystallography is the branch of science devoted to the study of molecular and crystalline structure and properties. The word ''crystallography'' is derived from the Ancient Greek word (; "clear ice, rock-crystal"), and (; "to write"). In J ...
, and materials science
Materials science is an interdisciplinary field of researching and discovering materials. Materials engineering is an engineering field of finding uses for materials in other fields and industries.
The intellectual origins of materials sci ...
, the coordination number, also called ligancy, of a central atom
Atoms are the basic particles of the chemical elements. An atom consists of a atomic nucleus, nucleus of protons and generally neutrons, surrounded by an electromagnetically bound swarm of electrons. The chemical elements are distinguished fr ...
in a molecule
A molecule is a group of two or more atoms that are held together by Force, attractive forces known as chemical bonds; depending on context, the term may or may not include ions that satisfy this criterion. In quantum physics, organic chemi ...
or crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macros ...
is the number of atoms, molecules or ions bonded to it. The ion/molecule/atom surrounding the central ion/molecule/atom is called a ligand
In coordination chemistry, a ligand is an ion or molecule with a functional group that binds to a central metal atom to form a coordination complex. The bonding with the metal generally involves formal donation of one or more of the ligand's el ...
. This number is determined somewhat differently for molecules than for crystals.
For molecules and polyatomic ions the coordination number of an atom is determined by simply counting the other atoms to which it is bonded (by either single or multiple bonds). For example, r(NH3)2Cl2Br2sup>− has Cr3+ as its central cation, which has a coordination number of 6 and is described as ''hexacoordinate''. The common coordination numbers are 4, 6 and 8.
Molecules, polyatomic ions and coordination complexes
In chemistry, coordination number, defined originally in 1893 by Alfred Werner, is the total number of neighbors of a central atom in a molecule or ion. The concept is most commonly applied tocoordination complex
A coordination complex is a chemical compound consisting of a central atom or ion, which is usually metallic and is called the ''coordination centre'', and a surrounding array of chemical bond, bound molecules or ions, that are in turn known as ' ...
es.
Simple and commonplace cases
The most common coordination number for ''d-''blocktransition metal
In chemistry, a transition metal (or transition element) is a chemical element in the d-block of the periodic table (groups 3 to 12), though the elements of group 12 (and less often group 3) are sometimes excluded. The lanthanide and actinid ...
complexes is 6. The coordination number does not distinguish the geometry of such complexes, i.e. octahedral vs trigonal prismatic.
For transition metal complexes, coordination numbers range from 2 (e.g., AuI in Ph3PAuCl) to 9 (e.g., ReVII in eH9sup>2−). Metals in the ''f''-block (the lanthanoids and actinoids) can accommodate higher coordination number due to their greater ionic radii and availability of more orbitals for bonding. Coordination numbers of 8 to 12 are commonly observed for ''f''-block elements. For example, with bidentate nitrate
Nitrate is a polyatomic ion with the chemical formula . salt (chemistry), Salts containing this ion are called nitrates. Nitrates are common components of fertilizers and explosives. Almost all inorganic nitrates are solubility, soluble in wa ...
ions as ligands, CeIV and ThIV form the 12-coordinate ions e(NO3)6sup>2− ( ceric ammonium nitrate) and h(NO3)6sup>2−. When the surrounding ligands are much smaller than the central atom, even higher coordination numbers may be possible. One computational chemistry study predicted a particularly stable ion composed of a central lead
Lead () is a chemical element; it has Chemical symbol, symbol Pb (from Latin ) and atomic number 82. It is a Heavy metal (elements), heavy metal that is density, denser than most common materials. Lead is Mohs scale, soft and Ductility, malleabl ...
ion coordinated with no fewer than 15 helium atoms. Among the Frank–Kasper phases, the packing of metallic atoms can give coordination numbers of up to 16. At the opposite extreme, steric shielding can give rise to unusually low coordination numbers. An extremely rare instance of a metal adopting a coordination number of 1 occurs in the terphenyl-based arylthallium(I) complex 2,6-Tipp2C6H3Tl, where Tipp is the 2,4,6-triisopropylphenyl group.
Polyhapto ligands
Coordination numbers become ambiguous when dealing with polyhapto ligands. For π-electron ligands such as the cyclopentadienide ion 5H5sup>−, alkenes and the cyclooctatetraenide ion 8H8sup>2−, the number of adjacent atoms in the π-electron system that bind to the central atom is termed the hapticity. Inferrocene
Ferrocene is an organometallic chemistry, organometallic compound with the formula . The molecule is a Cyclopentadienyl complex, complex consisting of two Cyclopentadienyl anion, cyclopentadienyl rings sandwiching a central iron atom. It is an o ...
the hapticity, ''η'', of each cyclopentadienide anion is five, Fe(''η''5-C5H5)2. Various ways exist for assigning the contribution made to the coordination number of the central iron atom by each cyclopentadienide ligand. The contribution could be assigned as one since there is one ligand, or as five since there are five neighbouring atoms, or as three since there are three electron pairs involved. Normally the count of electron pairs is taken.
Surfaces and reconstruction
The coordination numbers are well defined for atoms in the interior of acrystal lattice
In crystallography, crystal structure is a description of ordered arrangement of atoms, ions, or molecules in a crystal, crystalline material. Ordered structures occur from intrinsic nature of constituent particles to form symmetric patterns that ...
: one counts the nearest neighbors in all directions. The number of neighbors of an interior atom is termed the bulk coordination number. For surfaces, the number of neighbors is more limited, so the surface coordination number is smaller than the bulk coordination number. Often the surface coordination number is unknown or variable. The surface coordination number is also dependent on the Miller indices of the surface. In a body-centered cubic (BCC) crystal, the bulk coordination number is 8, whereas, for the (100) surface, the surface coordination number is 4.
Experimental determination
A common way to determine the coordination number of an atom is byX-ray crystallography
X-ray crystallography is the experimental science of determining the atomic and molecular structure of a crystal, in which the crystalline structure causes a beam of incident X-rays to Diffraction, diffract in specific directions. By measuring th ...
. Related techniques include neutron
The neutron is a subatomic particle, symbol or , that has no electric charge, and a mass slightly greater than that of a proton. The Discovery of the neutron, neutron was discovered by James Chadwick in 1932, leading to the discovery of nucle ...
or electron
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up qua ...
diffraction. The coordination number of an atom can be determined straightforwardly by counting nearest neighbors.
α-Aluminium has a regular cubic close packed structure, fcc, where each aluminium atom has 12 nearest neighbors, 6 in the same plane and 3 above and below and the coordination polyhedron is a cuboctahedron. α-Iron has a body centered cubic structure where each iron atom has 8 nearest neighbors situated at the corners of a cube.
The two most common allotropes of carbon have different coordination numbers. In diamond
Diamond is a Allotropes of carbon, solid form of the element carbon with its atoms arranged in a crystal structure called diamond cubic. Diamond is tasteless, odourless, strong, brittle solid, colourless in pure form, a poor conductor of e ...
, each carbon atom is at the centre of a regular tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
formed by four other carbon atoms, the coordination number is four, as for methane. Graphite
Graphite () is a Crystallinity, crystalline allotrope (form) of the element carbon. It consists of many stacked Layered materials, layers of graphene, typically in excess of hundreds of layers. Graphite occurs naturally and is the most stable ...
is made of two-dimensional layers in which each carbon is covalently bonded to three other carbons; atoms in other layers are further away and are not nearest neighbours, giving a coordination number of 3.
 For chemical compounds with regular lattices such as
For chemical compounds with regular lattices such as sodium chloride
Sodium chloride , commonly known as Salt#Edible salt, edible salt, is an ionic compound with the chemical formula NaCl, representing a 1:1 ratio of sodium and chloride ions. It is transparent or translucent, brittle, hygroscopic, and occurs a ...
and caesium chloride
Caesium chloride or cesium chloride is the inorganic compound with the formula Caesium, CsChloride, Cl. This colorless salt is an important source of caesium ions in a variety of niche applications. Its crystal structure forms a major structural ...
, a count of the nearest neighbors gives a good picture of the environment of the ions. In sodium chloride each sodium ion has 6 chloride ions as nearest neighbours (at 276 pm) at the corners of an octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
and each chloride ion has 6 sodium atoms (also at 276 pm) at the corners of an octahedron. In caesium chloride each caesium has 8 chloride ions (at 356 pm) situated at the corners of a cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...
and each chloride has eight caesium ions (also at 356 pm) at the corners of a cube.
Complications
International Union of Crystallography, IUCR, states that the coordination number of an atom in a crystalline solid depends on the chemical bonding model and the way in which the coordination number is calculated. In some compounds the metal-ligand bonds may not all be at the same distance. For example in PbCl2, the coordination number of Pb2+ depends on which chlorides are assigned as ligands. Seven chloride ligands have Pb-Cl distances of 280–309 pm. Two chloride ligands are more distant, with a Pb-Cl distances of 370 pm. Some metals have irregular structures. For example, zinc has a distorted hexagonal close packed structure. Regular hexagonal close packing of spheres would predict that each atom has 12 nearest neighbours and atriangular orthobicupola
In geometry, the triangular orthobicupola is one of the Johnson solids (). As the name suggests, it can be constructed by attaching two triangular cupolas () along their bases. It has an equal number of squares and triangles at each vertex; howe ...
(also called an anticuboctahedron or twinned cuboctahedron) coordination polyhedron. In zinc there are only 6 nearest neighbours at 266 pm in the same close packed plane with six other, next-nearest neighbours, equidistant, three in each of the close packed planes above and below at 291 pm. The coordination number of Zn can be assigned as 12 rather than 6. Similar considerations can be applied to the regular body centred cube structure where in addition to the 8 nearest neighbors there 6 more, approximately 15% more distant, and in this case the coordination number is often considered to be 14.
 In Nickel arsenide (NiAs) and several related compounds, the coordination number of the metal is ambiguous. The metal is bound to six As ligands, but also has two Ni---Ni contacts that could qualify as bonds.
In Nickel arsenide (NiAs) and several related compounds, the coordination number of the metal is ambiguous. The metal is bound to six As ligands, but also has two Ni---Ni contacts that could qualify as bonds. Two other examples of commonly-encountered chemicals are Fe2O3 and TiO2. Fe2O3 has a crystal structure that can be described as having a near close packed array of oxygen atoms with iron atoms filling two thirds of the octahedral holes. However each iron atom has 3 nearest neighbors and 3 others a little further away. The structure is quite complex, the oxygen atoms are coordinated to four iron atoms and the iron atoms in turn share vertices, edges and faces of the distorted octahedra. TiO2 has the
Two other examples of commonly-encountered chemicals are Fe2O3 and TiO2. Fe2O3 has a crystal structure that can be described as having a near close packed array of oxygen atoms with iron atoms filling two thirds of the octahedral holes. However each iron atom has 3 nearest neighbors and 3 others a little further away. The structure is quite complex, the oxygen atoms are coordinated to four iron atoms and the iron atoms in turn share vertices, edges and faces of the distorted octahedra. TiO2 has the rutile
Rutile is an oxide mineral composed of titanium dioxide (TiO2), the most common natural form of TiO2. Rarer polymorphs of TiO2 are known, including anatase, akaogiite, and brookite.
Rutile has one of the highest refractive indices at vis ...
structure. The titanium atoms 6-coordinate, 2 atoms at 198.3 pm and 4 at 194.6 pm, in a slightly distorted octahedron. The octahedra around the titanium atoms share edges and vertices to form a 3-D network. The oxide ions are 3-coordinate in a trigonal planar configuration.
Several propositions have been made to calculate a mean or « effective » coordination number (e.c.n. or ECoN) by adding all surrounding atoms with a weighting scheme, in that the atoms are not counted as full atoms, but as fractional atoms with a number between 0 and 1; this number is closer to zero when the atom is further away. Frequently a gap can be found in the distribution of the interatomic distance of the neighboring atoms: if the shortest distance to a neighboring atom is set equal to 1, then often further atoms are found at distances between 1 and 1.3, and after them follows a gap in which no atoms are found.
According to a proposition of G. Brunner and D. Schwarzenbach an atom at the distance of 1 obtains a weight 1, the first atom beyond the gap obtains zero weight, and all intermediate atoms are included with weights that are calculated from their distances by linear interpolation:
where is the distance to the closest atom, is the distance to the first atom beyond the gap and is the distance to the ''i''-th atom in the region between and . This method is however of no help when no clear gap can be discerned.
A mathematically unique method of calculation considers the domain of influence (also called Voronoi polyhedron, Wigner-Seitz cell or Dirichlet domain). The domain is constructed by connecting the atom in question with all surrounding atoms; the set of planes perpendicular to the connecting lines and passing through their midpoints forms the domain of influence, which is a convex polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices. The term "polyhedron" may refer either to a solid figure or to its boundary su ...
. In this way, a polyhedron face can be assigned to every neighboring atom, the area of the face serving as measure for the weighting. A value of 1 is assigned to the largest face. Other formulas have also been derived, for example: