|
Radial Distribution Function
In statistical mechanics, the radial distribution function, (or pair correlation function) g(r) in a system of particles (atoms, molecules, colloids, etc.), describes how density varies as a function of distance from a reference particle. If a given particle is taken to be at the origin ''O'', and if \rho = N/V is the average number density of particles, then the local time-averaged density at a distance r from ''O'' is \rho g(r). This simplified definition holds for a homogeneous and isotropic system. A more general case will be considered below. In simplest terms it is a measure of the probability of finding a particle at a distance of r away from a given reference particle, relative to that for an ideal gas. The general algorithm involves determining how many particles are within a distance of r and r+dr away from a particle. This general theme is depicted to the right, where the red particle is our reference particle, and the blue particles are those whose centers are with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Rdf Schematic
RDF may refer to: Science and technology Computing * Resource Description Framework, a W3C metadata standard used for graphing ** RDF Schema, its language Physics * Radial distribution function, describes how density varies as a function of distance from a reference particle * Direction finding, Radio direction finding, techniques used when searching for radio sources * Random dopant fluctuation * Reduced dimensions form, a canonical mechanism for solving two-state trajectories * Relative directivity factor, a figure of merit for directional receiving antennas Other technologies * Real degree of fermentation, attenuation of alcoholic beverages * Refuse-derived fuel Art, entertainment, and media * Radical Dance Faction, a band from the United Kingdom * RDF Media, a television production company * Robotech Defense Force, a character group in the US anime television series List of Robotech characters, ''Robotech'' * ''Rapid Deployment Force: Global Conflict'', a video game Militar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Indistinguishable Particle
In quantum mechanics, indistinguishable particles (also called identical or indiscernible particles) are particles that cannot be distinguished from one another, even in principle. Species of identical particles include, but are not limited to, elementary particles (such as electrons), composite subatomic particles (such as atomic nuclei), as well as atoms and molecules. Although all known indistinguishable particles only exist at the quantum scale, there is no exhaustive list of all possible sorts of particles nor a clear-cut limit of applicability, as explored in quantum statistics. They were first discussed by Werner Heisenberg and Paul Dirac in 1926. There are two main categories of identical particles: bosons, which can share quantum states, and fermions, which cannot (as described by the Pauli exclusion principle). Examples of bosons are photons, gluons, phonons, helium-4 nuclei and all mesons. Examples of fermions are electrons, neutrinos, quarks, protons, neutrons, and h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Pair Potential
In physics, a pair potential is a function that describes the potential energy of two interacting objects solely as a function of the distance between them. Some interactions, like Coulomb's law in electrodynamics or Newton's law of universal gravitation in mechanics naturally have this form for simple spherical objects. For other types of more complex interactions or objects it is useful and common to approximate the interaction by a pair potential, for example interatomic potentials in physics and computational chemistry that use approximations like the Lennard-Jones and Morse potentials. Functional form The total energy of a system of N objects at positions \vec_i, that interact through pair potential v is given by E=\frac12\sum_^N\sum_^Nv\left(\left, \vec_i - \vec_j\\right)\ . Equivalently, this can be expressed as E=\sum_^N\sum_^Nv\left(\left, \vec_i - \vec_j\\right)\ . This expression uses the fact that interaction is symmetric between particles i and j. It also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Virial Equation
In physics and chemistry, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most modern equations of state are formulated in the Helmholtz free energy. Equations of state are useful in describing the properties of pure substances and mixtures in liquids, gases, and solid states as well as the state of matter in the interior of stars. Though there are many equations of state, none accurately predicts properties of substances under all conditions. The quest for a universal equation of state has spanned three centuries. Overview At present, there is no single equation of state that accurately predicts the properties of all substances under all conditions. An example of an equation of state correlates densities of gases and liquids to temperatures and pressures, known as the ideal gas law, which is roughly accurate fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Jean-Pierre Hansen
Jean-Pierre Hansen FRS (born 10 May 1942) is a Luxembourgish chemist and an emeritus professor of the University of Cambridge. Education Hansen gained a PhD from Paris-Sud 11 University in 1969, the same year working as a staff scientist for the French National Centre for Scientific Research. Career and research In 1970, Hansen moved to the United States to do postdoctoral work at Cornell University before moving back to France in 1973 to work as an associate professor at Pierre and Marie Curie University. He became a full professor in 1977, and in 1980 moved to Grenoble to work as a visiting scientist at Institut Laue-Langevin. In 1986 he became research director at École Normale Supérieure de Lyon, and in 1987 founded the physics laboratory there. In 1990 the French Academy of Sciences awarded him the Grand Prix de l'Etat for his work, and between 1994 and 1997 he worked as a visiting professor at the physical chemistry department of the University of Oxford; he moved Corp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Potential Of Mean Force
When examining a system computationally one may be interested in knowing how the free energy changes as a function of some inter- or intramolecular coordinate (such as the distance between two atoms or a torsional angle). The free energy surface along the chosen coordinate is referred to as the potential of mean force (PMF). If the system of interest is in a solvent, then the PMF also incorporates the solvent effects. General description The PMF can be obtained in Monte Carlo or molecular dynamics Molecular dynamics (MD) is a computer simulation method for analyzing the Motion (physics), physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamics ( ... simulations to examine how a system's energy changes as a function of some specific reaction coordinate parameter. For example, it may examine how the system's energy changes as a function of the distance between two residues, or as a protei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
David Chandler (chemist)
David Chandler (October 15, 1944 – April 18, 2017) was an American physical chemist and a professor at the University of California, Berkeley. He was a member of the United States National Academy of Sciences and a winner of the Irving Langmuir Award. He published two books and over 300 scientific articles. Biography Chandler was born in New York City in 1944. He was the Bruce H. Mahan Professor of Chemistry at the University of California, Berkeley. He received his S.B. degree in chemistry from MIT in 1966, and his Ph.D. in chemical Physics at Harvard in 1969. He began his academic career as an assistant professor in 1970 at the University of Illinois Urbana–Champaign, rising through the ranks to become a full professor in 1977. Prior to joining the Berkeley faculty in 1986, Chandler spent two years as professor of chemistry at the University of Pennsylvania and was also a fellow of St John's College, Cambridge. Chandler's primary area of research was statistical mecha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Compressibility Equation
In statistical mechanics and thermodynamics the compressibility equation refers to an equation which relates the isothermal compressibility (and indirectly the pressure) to the structure of the liquid. It reads:kT\left(\frac\right)=1+\rho \int_V \mathrm \mathbf (r)-1where \rho is the number density, g(r) is the radial distribution function and kT\left(\frac\right) is the isothermal compressibility. Using the Fourier representation of the Ornstein-Zernike equation the compressibility equation can be rewritten in the form: \frac\left(\frac\right) = \frac=\frac=1-\rho\hat(0)=1-\rho \int c(r) \mathrm \mathbf where h(r) and c(r) are the indirect and direct correlation functions respectively. The compressibility equation is one of the many integral equations in statistical mechanics In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Compressibility
In thermodynamics and fluid mechanics, the compressibility (also known as the coefficient of compressibility or, if the temperature is held constant, the isothermal compressibility) is a measure of the instantaneous relative volume change of a fluid or solid as a response to a pressure (or mean stress) change. In its simple form, the compressibility \kappa (denoted in some fields) may be expressed as :\beta =-\frac\frac, where is volume and is pressure. The choice to define compressibility as the negative of the fraction makes compressibility positive in the (usual) case that an increase in pressure induces a reduction in volume. The reciprocal of compressibility at fixed temperature is called the isothermal bulk modulus. Definition The specification above is incomplete, because for any object or system the magnitude of the compressibility depends strongly on whether the process is isentropic or isothermal. Accordingly, isothermal compressibility is defined: :\beta_T=-\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Distribution (mathematics)
Distributions, also known as Schwartz distributions are a kind of generalized function in mathematical analysis. Distributions make it possible to derivative, differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative. Distributions are widely used in the theory of partial differential equations, where it may be easier to establish the existence of distributional solutions (weak solutions) than Solution of a differential equation, classical solutions, or where appropriate classical solutions may not exist. Distributions are also important in physics and engineering where many problems naturally lead to differential equations whose solutions or initial conditions are singular, such as the Dirac delta function, Dirac delta function. A Function (mathematics), function f is normally thought of as on the in the function Domain (function), domain by "sending" a point x in the domain t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Neutron Diffraction
Neutron diffraction or elastic neutron scattering is the application of neutron scattering to the determination of the atomic and/or magnetic structure of a material. A sample to be examined is placed in a beam of Neutron temperature, thermal or cold neutron radiation, neutrons to obtain a diffraction pattern that provides information of the structure of the material. The technique is similar to X-ray diffraction but due to their different scattering properties, neutrons and X-rays provide complementary information: X-Rays are suited for superficial analysis, strong x-rays from synchrotron radiation are suited for shallow depths or thin specimens, while neutrons having high penetration depth are suited for bulk samples.Measurement of residual stress in materials using neutrons IAEA, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
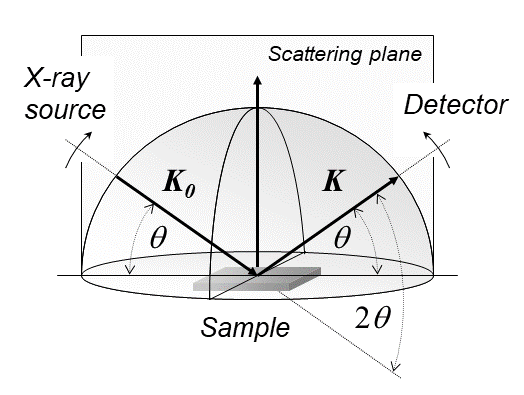 |
X-ray Diffraction
X-ray diffraction is a generic term for phenomena associated with changes in the direction of X-ray beams due to interactions with the electrons around atoms. It occurs due to elastic scattering, when there is no change in the energy of the waves. The resulting map of the directions of the X-rays far from the sample is called a diffraction pattern. It is different from X-ray crystallography which exploits X-ray diffraction to determine the arrangement of atoms in materials, and also has other components such as ways to map from experimental diffraction measurements to the positions of atoms. This article provides an overview of X-ray diffraction, starting with the early #History, history of x-rays and the discovery that they have the right spacings to be diffracted by crystals. In many cases these diffraction patterns can be #Introduction to x-ray diffraction theory, Interpreted using a single scattering or kinematical theory with conservation of energy (#Ewald's sphere, wave vecto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |