Conway Box Function

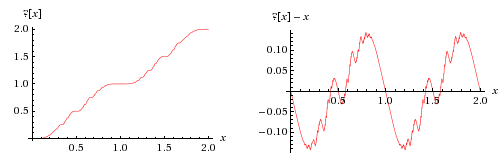
In mathematics, the Minkowski question-mark function, denoted , is a function with unusual fractal properties, defined by Hermann Minkowski in 1904. It maps quadratic irrational numbers to rational numbers on the unit interval, via an expression relating the continued fraction expansions of the quadratics to the binary expansions of the rationals, given by Arnaud Denjoy in 1938. It also maps rational numbers to dyadic rationals, as can be seen by a recursive definition closely related to the Stern–Brocot tree.

Definition and intuition

One way to define the question-mark function involves the correspondence between two different ways of representing fractional numbers using finite or infinite binary sequences. Most familiarly, a string of 0's and 1's with a single point mark ".", like "11.001001000011111..." can be interpreted as the binary representation of a number. In this case this number is
$2+1+\frac18+\frac1+\cdots=\pi.$
There is a different way of interpreting the same sequence, however, using continued fractions.
Interpreting the part before the point mark as a binary number in the same way, replace each consecutive block of 0's or 1's after the point by its run length, in this case generating the sequence ;2,1,2,1,4,5,\dots/math>. Then, use this sequence as the coefficients of a continued fraction:
$3+\frac\approx 3.365$

The question-mark function reverses this process: it translates the continued-fraction of a given real number into a run-length encoded binary sequence, and then reinterprets that sequence as a binary number. For instance, for the example above, $\operatorname(3.365\dots)=\pi$. To define this formally, if an irrational number $x$ has the (non-terminating) continued-fraction representation
x=a_0+\frac= _0;a_1,a_2,\dots/math>
then the value of the question-mark function on $x$ is defined as the value of the infinite series
$\operatorname(x) = a_0 + 2 \sum_^\infty \frac.$
In the same way, if a rational number $x$ has the terminating continued-fraction representation _0;a_1,a_2,\dots,a_m/math> then
the value of the question-mark function on $x$ is a finite sum,
$\operatorname(x) = a_0 + 2 \sum_^m \frac.$

Analogously to the way the question-mark function reinterprets continued fractions as binary numbers, the Cantor function can be understood as reinterpreting ternary numbers as binary numbers.

Self-symmetry

The question mark is clearly visually self-similar. A monoid of self-similarities may be generated by two operators and acting on the unit square and defined as follows:
\begin
S(x, y) &= \left( \frac x , \frac y 2 \right), \\ px R(x, y) &= (1 - x, 1 - y).
\end

Visually, shrinks the unit square to its bottom-left quarter, while performs a point reflection through its center.

A point on the graph of has coordinates for some in the unit interval. Such a point is transformed by and into another point of the graph, because satisfies the following identities for all :
\begin
\operatorname\left(\frac\right) &= \frac, \\ px \operatorname(1 - x) &= 1 - \operatorname(x).
\end

These two operators may be repeatedly combined, forming a monoid. A general element of the monoid is then
$S^ R S^ R S^ \cdots$

for positive integers . Each such element describes a self-similarity of the question-mark function. This monoid is sometimes called the '' period-doubling monoid'', and all period-doubling fractal curves have a self-symmetry described by it (the de Rham curve, of which the question mark is a special case, is a category of such curves). The elements of the monoid are in correspondence with the rationals, by means of the identification of with the continued fraction . Since both
$S : x \mapsto \frac$
and
$T : x \mapsto 1 - x$
are linear fractional transformations with integer coefficients, the monoid may be regarded as a subset of the modular group .

Quadratic irrationals

The question mark function provides a one-to-one mapping from the non-dyadic rationals to the quadratic irrationals, thus allowing an explicit proof of countability of the latter. These can, in fact, be understood to correspond to the periodic orbits for the dyadic transformation. This can be explicitly demonstrated in just a few steps.

Dyadic symmetry

Define two moves: a left move and a right move, valid on the unit interval $0\le x\le 1$ as
$L_D(x) = \frac$ and $L_C(x) = \frac$
and
$R_D(x) = \frac$ and $R_C(x) = \frac$
The question mark function then obeys a left-move symmetry
$L_D \circ ? = ? \circ L_C$
and a right-move symmetry
$R_D \circ ? = ? \circ R_C$
where $\circ$ denotes function composition. These can be arbitrary concatenated. Consider, for example, the sequence of left-right moves $LRLLR.$ Adding the subscripts C and D, and, for clarity, dropping the composition operator $\circ$ in all but a few places, one has:
$L_D R_D L_D L_D R_D \circ ? = ? \circ L_C R_C L_C L_C R_C$
Arbitrary finite-length strings in the letters L and R correspond to the dyadic rationals, in that every dyadic rational can be written as both $y=n/2^m$ for integer ''n'' and ''m'' and as finite length of bits $y=0.b_1b_2b_3\cdots b_m$ with $b_k\in \.$ Thus, every dyadic rational is in one-to-one correspondence with some self-symmetry of the question mark function.

Some notational rearrangements can make the above slightly easier to express. Let $g_0$ and $g_1$ stand for L and R. Function composition extends this to a monoid, in that one can write $g_=g_0g_1g_0$ and generally, $g_Ag_B=g_$ for some binary strings of digits ''A'', ''B'', where ''AB'' is just the ordinary concatenation of such strings. The dyadic monoid ''M'' is then the monoid of all such finite-length left-right moves. Writing $\gamma\in M$ as a general element of the monoid, there is a corresponding self-symmetry of the question mark function:
$\gamma_D\circ ?= ?\circ \gamma_C$

Isomorphism

An explicit mapping between the rationals and the dyadic rationals can be obtained providing a reflection operator
$r(x)=1-x$
and noting that both
$r\circ R_D\circ r = L_D$ and $r\circ R_C\circ r = L_C$
Since $r^2=1$ is the identity, an arbitrary string of left-right moves can be re-written as a string of left moves only, followed by a reflection, followed by more left moves, a reflection, and so on, that is, as $L^rL^rL^\cdots$ which is clearly isomorphic to $S^TS^TS^\cdots$ from above. Evaluating some explicit sequence of $L_D,R_D$ at the function argument $x=1$ gives a dyadic rational; explicitly, it is equal to $y=0.b_1b_2b_3\cdots b_m$ where each $b_k\in\$ is a binary bit, zero corresponding to a left move and one corresponding to a right move. The equivalent sequence of $L_C,R_C$ moves, evaluated at $x=1$ gives a rational number $p/q.$ It is explicitly the one provided by the continued fraction p/q= _1,a_2,a_3,\cdots,a_j/math> keeping in mind that it is a rational because the sequence $(a_1,a_2,a_3,\cdots,a_j)$ was of finite length. This establishes a one-to-one correspondence between the dyadic rationals and the rationals.

Periodic orbits of the dyadic transform

Consider now the periodic orbits of the dyadic transformation. These correspond to bit-sequences consisting of a finite initial "chaotic" sequence of bits $b_0,b_1,b_2,\cdots, b_$, followed by a repeating string $b_k,b_,b_,\cdots, b_$ of length $m$. Such repeating strings correspond to a rational number. This is easily made explicit. Write
$y=\sum_^ b_2^$
one then clearly has
$\sum_^\infty b_2^ = y\sum_^\infty 2^ = \frac$
Tacking on the initial non-repeating sequence, one clearly has a rational number. In fact, ''every'' rational number can be expressed in this way: an initial "random" sequence, followed by a cycling repeat. That is, the periodic orbits of the map are in one-to-one correspondence with the rationals.

Periodic orbits as continued fractions

Such periodic orbits have an equivalent periodic continued fraction, per the isomorphism established above. There is an initial "chaotic" orbit, of some finite length, followed by the a repeating sequence. The repeating sequence generates a periodic continued fraction satisfying $x=[a_n,a_,a_,\cdots,a_,x].$ This continued fraction has the form
$x = \frac$
with the $\alpha,\beta,\gamma,\delta$ being integers, and satisfying $\alpha \delta-\beta \gamma=\pm 1.$ Explicit values can be obtained by writing
$S\mapsto \begin 1 & 0\\ 1 & 1\end$
for the shift, so that
$S^n\mapsto \begin 1 & 0\\ n & 1\end$
while the reflection is given by
$T\mapsto \begin -1 & 1\\ 0 & 1\end$
so that $T^2=I$. Both of these matrices are unimodular, arbitrary products remain unimodular, and result in a matrix of the form
$S^TS^T\cdots TS^ = \begin \alpha & \beta\\ \gamma & \delta\end$
giving the precise value of the continued fraction. As all of the matrix entries are integers, this matrix belongs to the projective modular group $PSL(2,\mathbb).$

Solving explicitly, one has that $\gamma x^2 + (\delta-\alpha)x-\beta=0.$ It is not hard to verify that the solutions to this meet the definition of quadratic irrationals. In fact, every quadratic irrational can be expressed in this way. Thus the quadratic irrationals are in one-to-one correspondence with the periodic orbits of the dyadic transform, which are in one-to-one correspondence with the (non-dyadic) rationals, which are in one-to-one correspondence with the dyadic rationals. The question mark function provides the correspondence in each case.

Properties of

The question-mark function is a strictly increasing and continuous, but not absolutely continuous function. The derivative is defined almost everywhere, and can take on only two values, 0 (its value almost everywhere, including at all rational numbers) and $+\infty$. There are several constructions for a measure that, when integrated, yields the question-mark function. One such construction is obtained by measuring the density of the Farey numbers on the real number line. The question-mark measure is the prototypical example of what are sometimes referred to as multi-fractal measures.

The question-mark function maps rational numbers to dyadic rational numbers, meaning those whose base two representation terminates, as may be proven by induction from the recursive construction outlined above. It maps quadratic irrationals to non-dyadic rational numbers. In both cases it provides an order isomorphism between these sets, making concrete Cantor's isomorphism theorem according to which every two unbounded countable dense linear orders are order-isomorphic. It is an odd function, and satisfies the functional equation ; consequently is an odd periodic function with period one. If is irrational, then is either algebraic of degree greater than two, or transcendental.

The question-mark function has fixed points at 0, and 1, and at least two more, symmetric about the midpoint. One is approximately 0.42037.
It was conjectured by Moshchevitin that they were the only 5 fixed points.

In 1943, Raphaël Salem raised the question of whether the Fourier–Stieltjes coefficients of the question-mark function vanish at infinity. In other words, he wanted to know whether or not
$\lim_\int_0^1 e^ \, \operatorname(x)=0.$

This was answered affirmatively by Jordan and Sahlsten, as a special case of a result on Gibbs measures.

The graph of Minkowski question mark function is a special case of fractal curves known as de Rham curves.

Algorithm

The recursive definition naturally lends itself to an algorithm for computing the function to any desired degree of accuracy for any real number, as the following C function demonstrates. The algorithm descends the Stern–Brocot tree in search of the input , and sums the terms of the binary expansion of on the way. As long as the loop invariant remains satisfied there is no need to reduce the fraction , since it is already in lowest terms. Another invariant is . The for loop in this program may be analyzed somewhat like a while loop, with the conditional break statements in the first three lines making out the condition. The only statements in the loop that can possibly affect the invariants are in the last two lines, and these can be shown to preserve the truth of both invariants as long as the first three lines have executed successfully without breaking out of the loop. A third invariant for the body of the loop (up to floating point precision) is , but since is halved at the beginning of the loop before any conditions are tested, our conclusion is only that at the termination of the loop.

To prove termination, it is sufficient to note that the sum q + s increases by at least 1 with every iteration of the loop, and that the loop will terminate when this sum is too large to be represented in the primitive C data type long. However, in practice, the conditional break when y + d

y is what ensures the termination of the loop in a reasonable amount of time.

/* Minkowski's question-mark function */
double minkowski(double x)

Probability distribution

Restricting the Minkowski question mark function to ?: ,1→ ,1 it can be used as the cumulative distribution function of a singular distribution on the unit interval. This distribution is symmetric about its midpoint, with raw moments of about ''m''₁ = 0.5, ''m''₂ = 0.290926, ''m''₃ = 0.186389 and ''m''₄ = 0.126992, and so a mean and median of 0.5, a standard deviation of about 0.2023, a skewness of 0, and an excess kurtosis about -1.147.

See also

* Pompeiu derivative

References

Notes

Historical sources

*
*

Bibliography

*
*
*
*
*
*
*; reprinted by Dover Publications, 1997
*
*
*

Further reading

*
*
*
*
*
*
*

External links

An extensive bibliography list

*{{mathworld, urlname=MinkowskisQuestionMarkFunction, title=Minkowski's Question Mark Function, mode=cs2

Simple IEEE 754 implementation in C++

De Rham curves
Continued fractions
Special functions
Theory of continuous functions
Articles with example C code
Hermann Minkowski