Contraction Hierarchy

In computer science, the method of contraction hierarchies is a speed-up technique for finding the shortest-path in a graph. The most intuitive applications are car-navigation systems: a user wants to drive from $A$ to $B$ using the quickest possible route. The metric optimized here is the travel time. Intersections are represented by vertices, the road sections connecting them by edges. The edge weights represent the time it takes to drive along this segment of the road. A path from $A$ to $B$ is a sequence of edges (road sections); the shortest path is the one with the minimal sum of edge weights among all possible paths. The shortest path in a graph can be computed using Dijkstra's algorithm but, given that road networks consist of tens of millions of vertices, this is impractical. Contraction hierarchies is a speed-up method optimized to exploit properties of graphs representing road networks. The speed-up is achieved by creating shortcuts in a preprocessing phase which are then used during a shortest-path query to skip over "unimportant" vertices. This is based on the observation that road networks are highly hierarchical. Some intersections, for example highway junctions, are "more important" and higher up in the hierarchy than for example a junction leading into a dead end. Shortcuts can be used to save the precomputed distance between two important junctions such that the algorithm doesn't have to consider the full path between these junctions at query time. Contraction hierarchies do not know about which roads humans consider "important" (e.g. highways), but they are provided with the graph as input and are able to assign importance to vertices using heuristics.

Contraction hierarchies are not only applied to speed-up algorithms in car-navigation systems but also in web-based route planners, traffic simulation, and logistics optimization. Implementations of the algorithm are publicly available as open source software.

Algorithm

The contraction hierarchies (CH) algorithm is a two-phase approach to the shortest path problem consisting of a preprocessing phase and a query phase. As road networks change rather infrequently, more time (seconds to hours) can be used to once precompute some calculations before queries are to be answered. Using this precomputed data, many queries can be answered taking very little time (microseconds) each. CHs rely on shortcuts to achieve this speedup. A shortcut connects two vertices $u$ and $v$ not adjacent in the original graph. Its edge weight is the sum of the edge weights on the shortest $u$-$v$ path.

Consider two large cities connected by a highway. Between these two cities, there is a multitude of junctions leading to small villages and suburbs. Most drivers want to get from one city to the other – maybe as part of a larger route – and not take one of the exits on the way. In the graph representing this road layout, each intersection is represented by a node and edges are created between neighboring intersections. To calculate the distance between these two cities, the algorithm has to traverse all the edges along the way, adding up their length. Precomputing this distance once and storing it in an additional edge created between the two large cities will save calculations each time this highway has to be evaluated in a query. This additional edge is called a "shortcut" and has no counterpart in the real world. The contraction hierarchies algorithm has no knowledge about road types but is able to determine which shortcuts have to be created using the graph alone as input.

Preprocessing phase

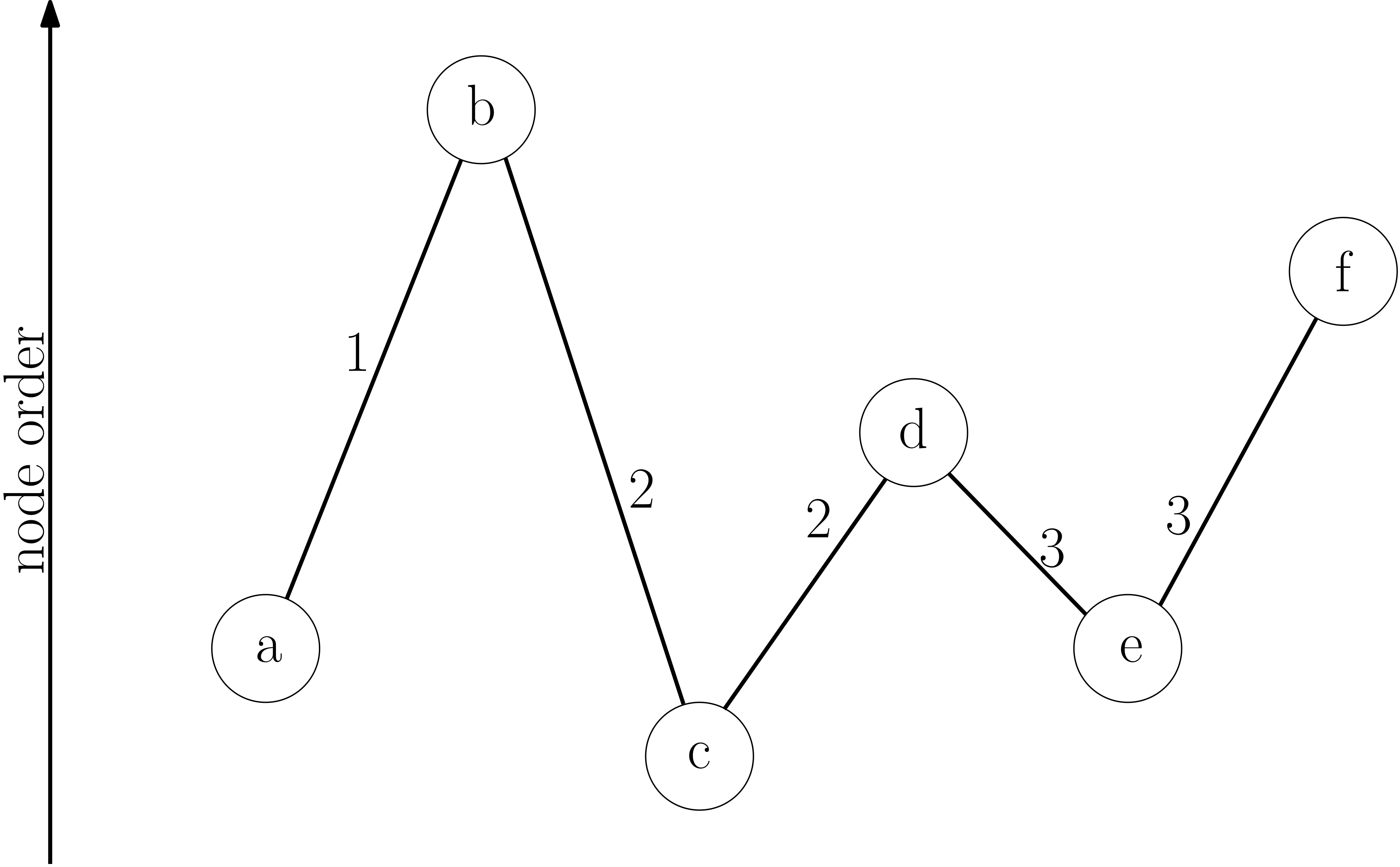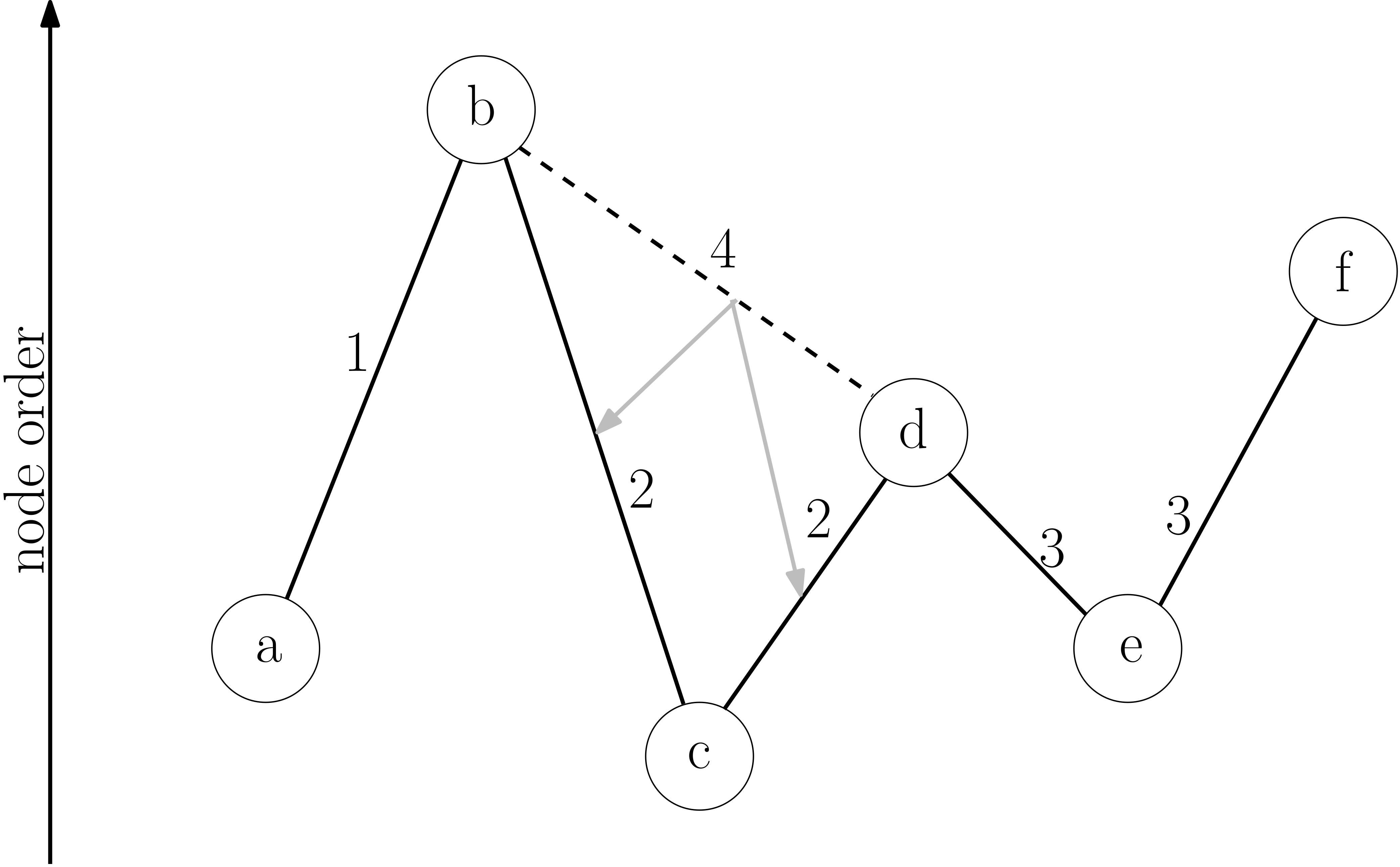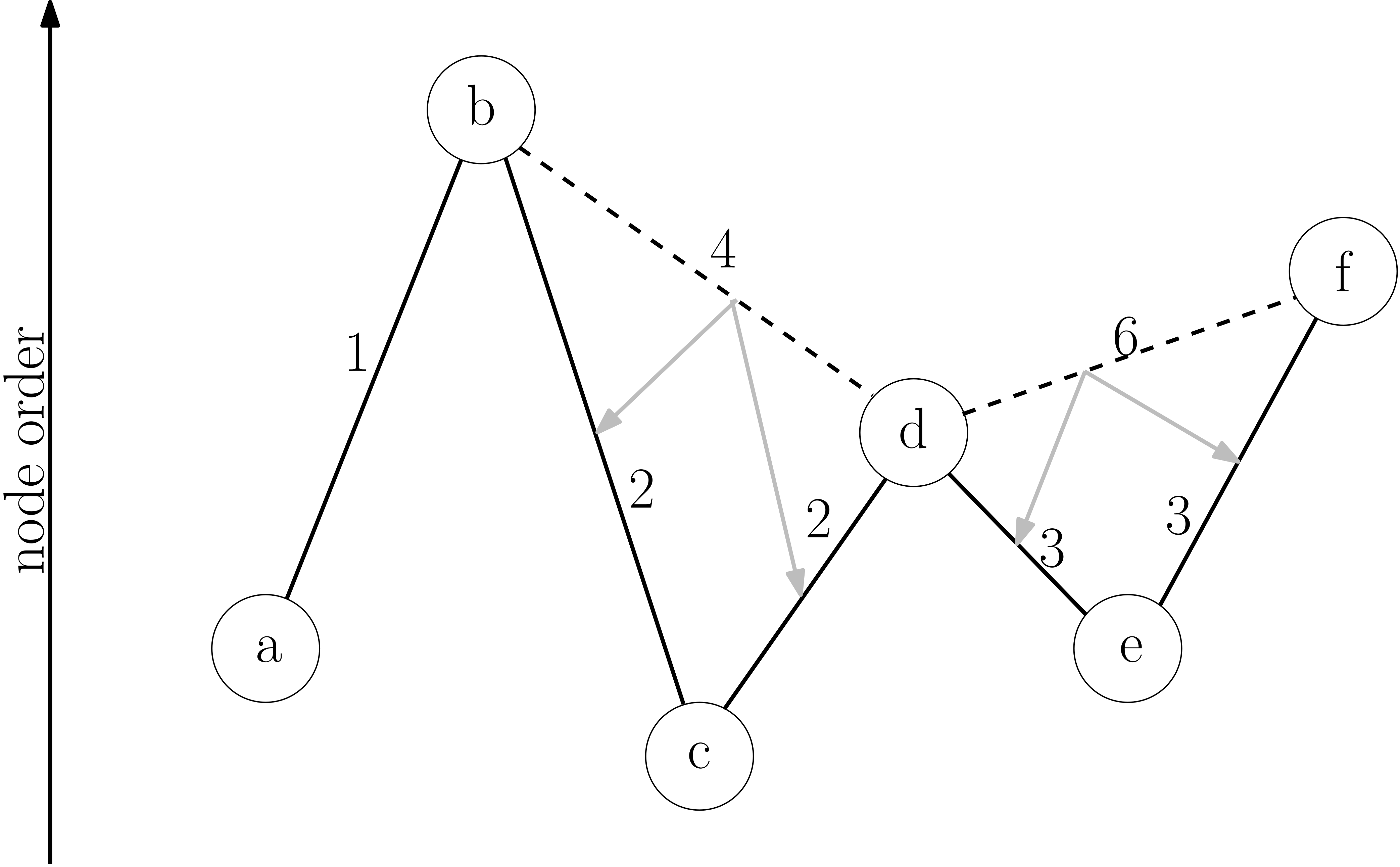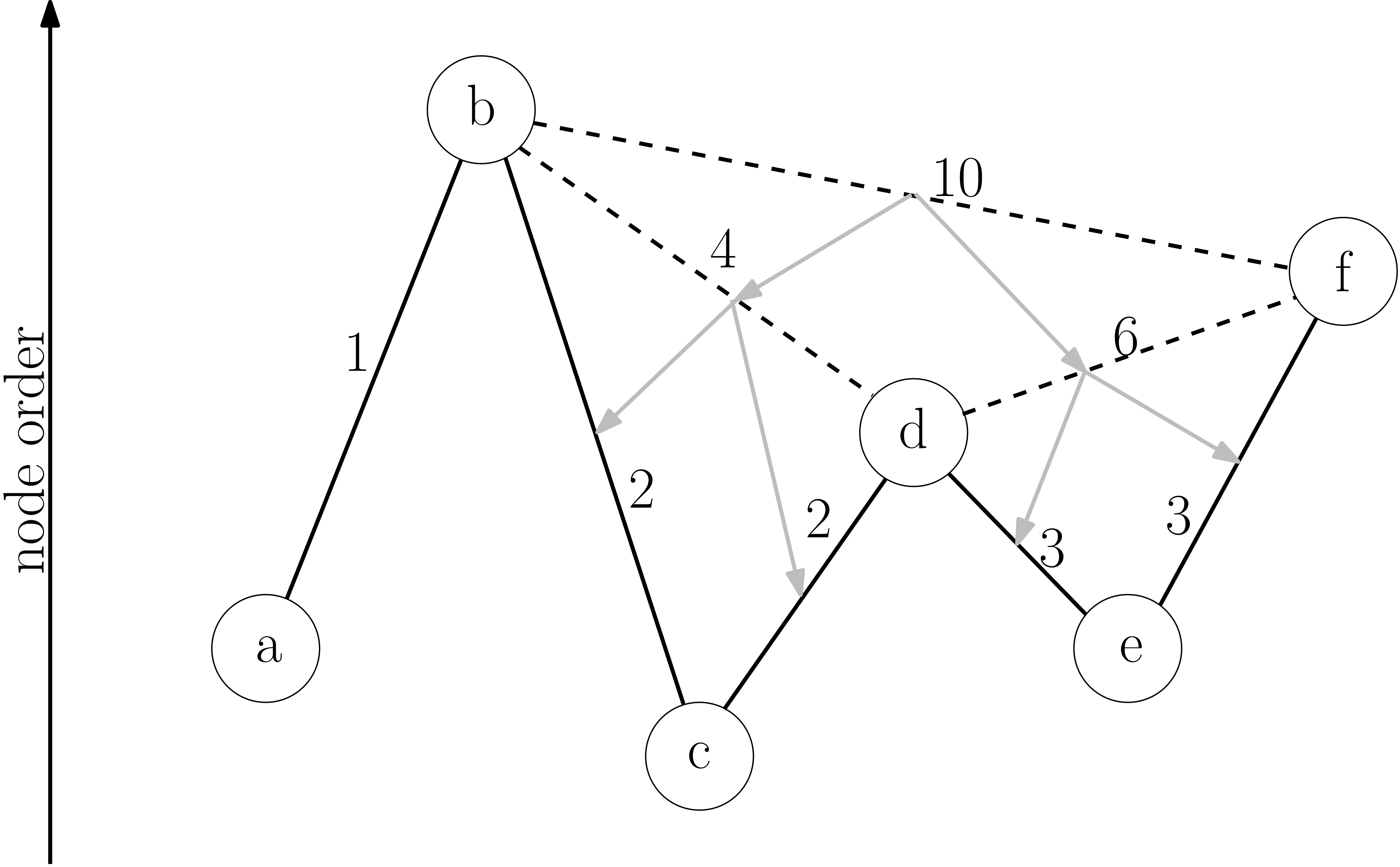
The CH algorithm relies on shortcuts created in the preprocessing phase to reduce the search space – that is the number of vertices CH has to look at, at query time. To achieve this, iterative vertex contractions are performed. When contracting a vertex $v$ it is temporarily removed from the graph $G$, and a shortcut is created between each pair $\$ of neighboring vertices if the shortest path from $u$ to $w$ contains $v$. The process of determining if the shortest path between $u$ and $w$ contains $v$ is called witness search. It can be performed for example by computing a path from $u$ to $w$ using a forward search using only not yet contracted nodes.

Node order

The vertices of the input graph have to be contracted in a way which minimizes the number of edges added to the graph by contractions. As optimal node ordering is NP-complete, heuristics are used.

''Bottom-up'' and ''top-down'' heuristics exist. On one hand, the computationally cheaper bottom-up heuristics decide the order in which to contract the vertices in a greedy fashion; this means the order is not known in advance but rather the next node is selected for contraction after the previous contraction has been completed. Top-down heuristics on the other hand precompute the whole node ordering before the first node is contracted. This yields better results but needs more preprocessing time.

In ''bottom-up'' heuristics, a combination of factors is used to select the next vertex for contraction. As the number of shortcuts is the primary factor that determines preprocessing and query runtime, we want to keep it as small as possible. The most important term by which to select the next node for contraction is therefore the net number of edges added when contracting a node $x$. This is defined as $A(x)-, \,$ where $A(x)$ is the number of shortcuts that would be created if $x$ were to be contracted and $, \,$ is the number of edges incident to $x$. Using this criterion alone, a linear path would result in a linear hierarchy (many levels) and no created shortcuts. By considering the number of nearby vertices that are already contracted, a uniform contraction and a flat hierarchy (less levels) is achieved. This can, for example, be done by maintaining a counter for each node that is incremented each time a neighboring vertex is contracted. Nodes with lower counters are then preferred to nodes with higher counters.

''Top-down'' heuristics, on the other hand, yield better results but need more preprocessing time. They classify vertices that are part of many shortest paths as more important than those that are only needed for a few shortest paths. This can be approximated using nested dissections. To compute a nested dissection, one recursively separates a graph into two parts, which are themselves then separated into two parts and so on. That is, find a subset of nodes $S \subseteq V$ which when removed from the graph $G$ separate $G$ into two disjunct pieces $G_1, G_2$ of approximately equal size such that $S \cup G_1 \cup G_2 = G$. Place all nodes $v \in S$ ''last'' in the node ordering and then recursively compute the nested dissection for $G_1$ and $G_2$, the intuition being that all queries from one half of the graph to the other half of the graph need to pass through the small separator and therefore nodes in this separator are of high importance. Nested dissections can be efficiently calculated on road networks because of their small separators.

Query phase

In the query phase, a bidirectional search is performed starting from the starting node $s$ and the target node $t$ on the original graph augmented by the shortcuts created in the preprocessing phase. The most important vertex on the shortest path between $s$ and $t$ will be either $s$ or $t$ themselves or more important than both $s$ and $t$. Therefore the vertex $u$ minimizing $\mathrm(s, u) + \mathrm(u, t)$ is on the shortest $s-t$ path in the original graph and $\mathrm(s, u) + \mathrm(u, t) = \mathrm(s, t)$ holds. This, in combination with how shortcuts are created, means that both forward and backward search only need to relax edges leading to more important nodes (upwards) in the hierarchy which keeps the search space small. In all up-(down-up)-down paths, the inner (down-up) can be skipped, because a shortcut has been created in the preprocessing stage.

Path retrieval

A CH query, as described above, yields the time or distance from $s$ to $t$ but not the actual path. To obtain the list of edges (roads) on the shortest path, the shortcuts taken have to be unpacked. Each shortcut is the concatenation of two edges: either two edges of the original graph, or two shortcuts, or one original edge and one shortcut. Storing the middle vertex of each shortcut during contraction enables linear-time recursive unpacking of the shortest route.

Customized contraction hierarchies

If the edge weights are changed more often than the network topology, CH can be extended to a three-phase approach by including a customization phase between the preprocessing and query phase. This can be used for example to switch between shortest distance and shortest time or include current traffic information as well as user preferences like avoiding certain types of roads (ferries, highways, ...). In the preprocessing phase, most of the runtime is spent on computing the order in which the nodes are contracted. This sequence of contraction operations in the preprocessing phase can be saved for when they are later needed in the customization phase. Each time the metric is customized, the contractions can then be efficiently applied in the stored order using the custom metric. Additionally, depending on the new edge weights it may be necessary to recompute some shortcuts. For this to work, the contraction order has to be computed using metric-independent nested dissections.

Extensions and applications

CHs as described above search for a shortest path from one starting node to one target node. This is called ''one-to-one'' shortest path and is used for example in car-navigation systems. Other applications include matching GPS traces to road segments and speeding up traffic simulators which have to consider the likely routes taken by all drivers in a network. In route prediction one tries to estimate where a vehicle is likely headed by calculating how well its current and past positions agree with a shortest path from its starting point to any possible target. This can be efficiently done using CHs.

In ''one-to-many'' scenarios, a starting node $s$ and a set of target nodes $T$ are given and the distance $\mathrm(s, t)$ for all $t \in T$ has to be computed. The most prominent application for one-to-many queries are point-of-interest searches. Typical examples include finding the closest gas station, restaurant or post office using actual travel time instead of geographical distance as metric.

In the ''many-to-many'' shortest path scenario, a set of starting nodes $S$ and a set of target nodes $T$ are given and the distance $\mathrm(s_i, t_i)$ for all $(s_i, t_j) \in S \times T$ has to be computed. This is used for example in logistic applications. CHs can be extended to many-to-many queries in the following manner. First, perform a backward upward search from each $t_j \in T$. For each vertex $u$ scanned during this search, one stores $\mathrm(t_j, u)$ in a bucket $\beta (u)$. Then, one runs a forward upward search from each $s_i \in S$, checking for each non-empty bucket, whether the route over the corresponding vertex improves any best distance. That is, if $\mathrm(s_i, u) + \mathrm(u, t_j) < \mathrm(s_i, t_j)$ for any $(s_i, t_j) \in S \times T$.

Some applications even require ''one-to-all'' computations, i.e., finding the distances from a source vertex $s$ to all other vertices in the graph. As Dijkstra’s algorithm visits each edge exactly once and therefore runs in linear time it is theoretically optimal. Dijkstra’s algorithm, however, is hard to parallelize and is not cache-optimal because of its bad locality. CHs can be used for a more cache-optimal implementation. For this, a forward upward search from $s$ followed by a downward scan over all nodes in the shortcut-enriched graph is performed. The later operation scans through memory in a linear fashion, as the nodes are processed in decreasing order of importance and can therefore be placed in memory accordingly. Note, that this is possible because the order in which the nodes are processed in the second phase is independent of the source node $s$.

In production, car-navigation systems should be able to compute fastest travel routes using predicted traffic information and display alternative routes. Both can be done using CHs. The former is called routing with time-dependent networks where the travel time of a given edge is no longer constant but rather a function of the time of day when entering the edge. Alternative routes need to be smooth-looking, significantly different from the shortest path but not significantly longer.

CHs can be extended to optimize multiple metrics at the same time; this is called ''multi-criteria'' route planning. For example one could minimize both travel cost and time. Another example are electric vehicles for which the available battery charge constrains the valid routes as the battery may not run empty.

Theory

A number of bounds have been established on the preprocessing and query performance of contraction hierarchies. In the following let $n$ be the number of vertices in the graph, $m$ the number of edges, $h$ the highway dimension, $D$ the graph diameter, $td$ is the tree-depth and $tw$ is the tree-width.

The first analysis of contraction hierarchy performance relies in part on a quantity known as the ''highway dimension''. While the definition of this quantity is technical, intuitively a graph has a small highway dimension if for every $r>0$ there is a sparse set of vertices $S_r$ such that every shortest path of length greater than $r$ includes a vertex from $S_r$. Calculating the exact value of the highway dimension is NP-hard, but for grids it is known that the highway dimension $h\in\Theta(\sqrt)$.

An alternative analysis was presented in the Customizable Contraction Hierarchy line of work. Query running times can be bounded by $O(td^2)$. As the tree-depth can be bounded in terms of the tree-width, $O((tw \log n)^2)$ is also a valid upper bound. The main source is but the consequences for the worst case running times are better detailed in.

Preprocessing Performance

Query Performance

References

{{reflist

External links

Open source implementations

* https://www.graphhopper.com/
* https://github.com/ifsttar/Tempus
* https://github.com/RoutingKit/RoutingKit
* http://project-osrm.org/
*http://www.opentripplanner.org/

Graph algorithms
Search algorithms
Routing algorithms