Connected (graph Theory) on:
[Wikipedia]
[Google]
[Amazon]

 In
In
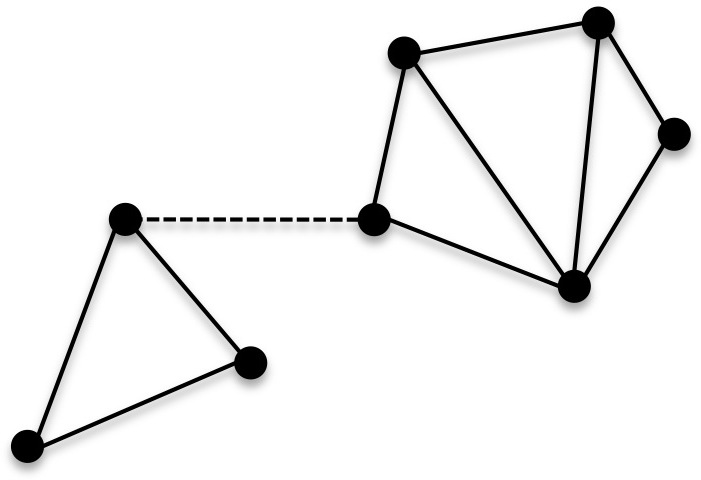
 In an undirected graph , two '' vertices'' and are called connected if contains a path from to . Otherwise, they are called disconnected. If the two vertices are additionally connected by a path of length , i.e. by a single edge, the vertices are called adjacent.
A graph is said to be connected if every pair of vertices in the graph is connected. This means that there is a path between every pair of vertices. An undirected graph that is not connected is called disconnected. An undirected graph ''G'' is therefore disconnected if there exist two vertices in ''G'' such that no path in ''G'' has these vertices as endpoints. A graph with just one vertex is connected. An edgeless graph with two or more vertices is disconnected.
A directed graph is called weakly connected if replacing all of its directed edges with undirected edges produces a connected (undirected) graph. It is unilaterally connected or unilateral (also called semiconnected) if it contains a directed path from to or a directed path from to for every pair of vertices . It is strongly connected, or simply strong, if it contains a directed path from to and a directed path from to for every pair of vertices .
In an undirected graph , two '' vertices'' and are called connected if contains a path from to . Otherwise, they are called disconnected. If the two vertices are additionally connected by a path of length , i.e. by a single edge, the vertices are called adjacent.
A graph is said to be connected if every pair of vertices in the graph is connected. This means that there is a path between every pair of vertices. An undirected graph that is not connected is called disconnected. An undirected graph ''G'' is therefore disconnected if there exist two vertices in ''G'' such that no path in ''G'' has these vertices as endpoints. A graph with just one vertex is connected. An edgeless graph with two or more vertices is disconnected.
A directed graph is called weakly connected if replacing all of its directed edges with undirected edges produces a connected (undirected) graph. It is unilaterally connected or unilateral (also called semiconnected) if it contains a directed path from to or a directed path from to for every pair of vertices . It is strongly connected, or simply strong, if it contains a directed path from to and a directed path from to for every pair of vertices .
 In
In mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements (nodes or edges) that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network.
Connected vertices and graphs
Components and cuts
A connected component is a maximal connected subgraph of an undirected graph. Each vertex belongs to exactly one connected component, as does each edge. A graph is connected if and only if it has exactly one connected component. The strong components are the maximal strongly connected subgraphs of a directed graph. A vertex cut or separating set of a connected graph is a set of vertices whose removal renders disconnected. The vertex connectivity (where is not a complete graph) is the size of a minimal vertex cut. A graph is called '-vertex-connected or '-connected if its vertex connectivity is or greater. More precisely, any graph (complete or not) is said to be ''-vertex-connected'' if it contains at least vertices, but does not contain a set of vertices whose removal disconnects the graph; and is defined as the largest such that is -connected. In particular, a complete graph with vertices, denoted , has no vertex cuts at all, but . A vertex cut for two vertices and is a set of vertices whose removal from the graph disconnects and . The local connectivity is the size of a smallest vertex cut separating and . Local connectivity is symmetric for undirected graphs; that is, . Moreover, except for complete graphs, equals the minimum of over all nonadjacent pairs of vertices . -connectivity is also called '' biconnectivity'' and -connectivity is also called ''triconnectivity''. A graph which is connected but not -connected is sometimes called ''separable''. Analogous concepts can be defined for edges. In the simple case in which cutting a single, specific edge would disconnect the graph, that edge is called a '' bridge''. More generally, an edge cut of is a set of edges whose removal renders the graph disconnected. The '' edge-connectivity'' is the size of a smallest edge cut, and the local edge-connectivity of two vertices is the size of a smallest edge cut disconnecting from . Again, local edge-connectivity is symmetric. A graph is called ''-edge-connected'' if its edge connectivity is or greater. A graph is said to be ''maximally connected'' if its connectivity equals its minimum degree. A graph is said to be ''maximally edge-connected'' if its edge-connectivity equals its minimum degree.Super- and hyper-connectivity
A graph is said to be ''super-connected'' or ''super-κ'' if every minimum vertex cut isolates a vertex. A graph is said to be ''hyper-connected'' or ''hyper-κ'' if the deletion of each minimum vertex cut creates exactly two components, one of which is an isolated vertex. A graph is ''semi-hyper-connected'' or ''semi-hyper-κ'' if any minimum vertex cut separates the graph into exactly two components. More precisely: a connected graph is said to be ''super-connected'' or ''super-κ'' if all minimum vertex-cuts consist of the vertices adjacent with one (minimum-degree) vertex. A connected graph is said to be ''super-edge-connected'' or ''super-λ'' if all minimum edge-cuts consist of the edges incident on some (minimum-degree) vertex. A cutset of is called a non-trivial cutset if does not contain the neighborhood of any vertex . Then the ''superconnectivity'' κ1 of G is: : κ1(G) = min. A non-trivial edge-cut and the ''edge-superconnectivity'' λ1(G) are defined analogously.Menger's theorem
One of the most important facts about connectivity in graphs is Menger's theorem, which characterizes the connectivity and edge-connectivity of a graph in terms of the number of independent paths between vertices. If and are vertices of a graph , then a collection of paths between and is called independent if no two of them share a vertex (other than and themselves). Similarly, the collection is edge-independent if no two paths in it share an edge. The number of mutually independent paths between and is written as , and the number of mutually edge-independent paths between and is written as . Menger's theorem asserts that for distinct vertices ''u'',''v'', equals , and if ''u'' is also not adjacent to ''v'' then equals . This fact is actually a special case of the max-flow min-cut theorem.Computational aspects
The problem of determining whether two vertices in a graph are connected can be solved efficiently using a search algorithm, such as breadth-first search. More generally, it is easy to determine computationally whether a graph is connected (for example, by using a disjoint-set data structure), or to count the number of connected components. A simple algorithm might be written in pseudo-code as follows: #Begin at any arbitrary node of the graph, #Proceed from that node using either depth-first or breadth-first search, counting all nodes reached. #Once the graph has been entirely traversed, if the number of nodes counted is equal to the number of nodes of , the graph is connected; otherwise it is disconnected. By Menger's theorem, for any two vertices and in a connected graph , the numbers and can be determined efficiently using the max-flow min-cut algorithm. The connectivity and edge-connectivity of can then be computed as the minimum values of and , respectively. In computational complexity theory, SL is the class of problemslog-space reducible
In computational complexity theory, a log-space reduction is a reduction computable by a deterministic Turing machine using logarithmic space. Conceptually, this means it can keep a constant number of pointers into the input, along with a logari ...
to the problem of determining whether two vertices in a graph are connected, which was proved to be equal to L by Omer Reingold in 2004. Hence, undirected graph connectivity may be solved in space.
The problem of computing the probability that a Bernoulli random graph is connected is called network reliability and the problem of computing whether two given vertices are connected the ST-reliability problem. Both of these are #P-hard.
Number of connected graphs
The number of distinct connected labeled graphs with ''n'' nodes is tabulated in the On-Line Encyclopedia of Integer Sequences as sequence . The first few non-trivial terms areExamples
* The vertex- and edge-connectivities of a disconnected graph are both . * -connectedness is equivalent to connectedness for graphs of at least 2 vertices. * The complete graph on vertices has edge-connectivity equal to . Every other simple graph on vertices has strictly smaller edge-connectivity. * In a tree, the local edge-connectivity between every pair of vertices is .Bounds on connectivity
* The vertex-connectivity of a graph is less than or equal to its edge-connectivity. That is, . Both are less than or equal to the minimum degree of the graph, since deleting all neighbors of a vertex of minimum degree will disconnect that vertex from the rest of the graph. * For a vertex-transitive graph of degree , we have: . * For a vertex-transitive graph of degree , or for any (undirected) minimal Cayley graph of degree , or for any symmetric graph of degree , both kinds of connectivity are equal: .Other properties
* Connectedness is preserved by graph homomorphisms. * If is connected then its line graph is also connected. * A graph is -edge-connected if and only if it has an orientation that is strongly connected. * Balinski's theorem states that the polytopal graph (-skeleton
A skeleton is the structural frame that supports the body of an animal. There are several types of skeletons, including the exoskeleton, which is the stable outer shell of an organism, the endoskeleton, which forms the support structure inside ...
) of a -dimensional convex polytope is a -vertex-connected graph. Steinitz's previous theorem that any 3-vertex-connected planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross ...
is a polytopal graph (Steinitz theorem
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar gra ...
) gives a partial converse.
* According to a theorem of G. A. Dirac, if a graph is -connected for , then for every set of vertices in the graph there is a cycle that passes through all the vertices in the set.. The converse is true when .
See also
* Algebraic connectivity * Cheeger constant (graph theory) * Dynamic connectivity, Disjoint-set data structure * Expander graph * Strength of a graphReferences
{{reflist