cissoid of Diocles on:
[Wikipedia]
[Google]
[Amazon]

 In
In
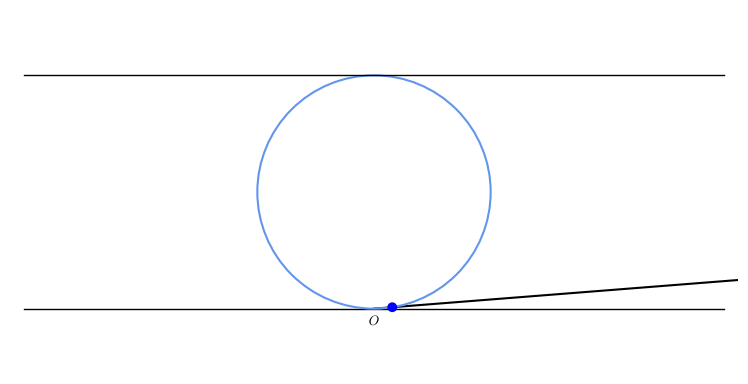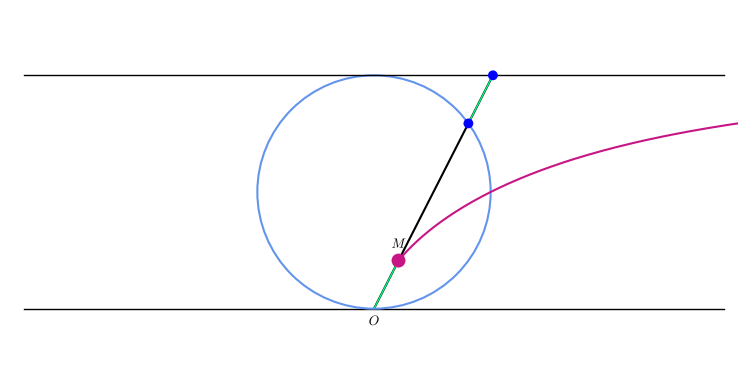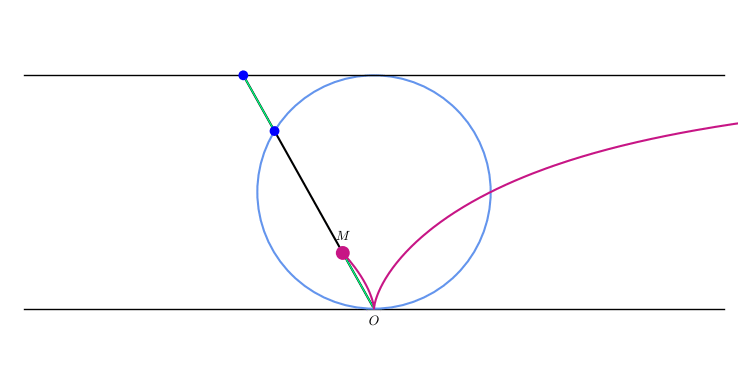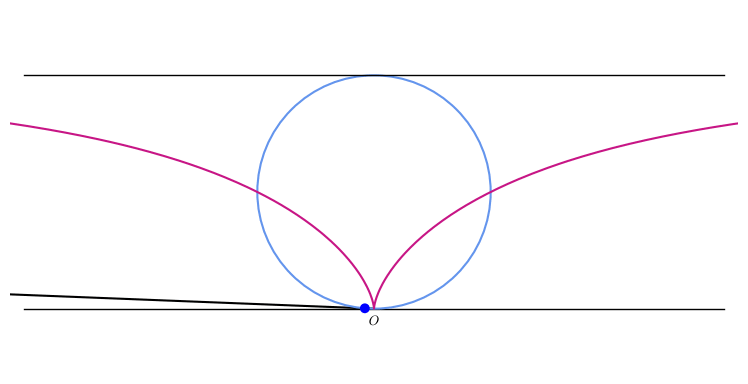
 A compass-and-straightedge construction of various points on the cissoid proceeds as follows. Given a line and a point not on , construct the line through parallel to . Choose a variable point on , and construct , the orthogonal projection of on , then , the orthogonal projection of on . Then the cissoid is the locus of points .
To see this, let be the origin and the line as above. Let be the point ; then is and the equation of the line is . The line through perpendicular to is
:
To find the point of intersection , set in this equation to get
:
which are the parametric equations given above.
While this construction produces arbitrarily many points on the cissoid, it cannot trace any continuous segment of the curve.
A compass-and-straightedge construction of various points on the cissoid proceeds as follows. Given a line and a point not on , construct the line through parallel to . Choose a variable point on , and construct , the orthogonal projection of on , then , the orthogonal projection of on . Then the cissoid is the locus of points .
To see this, let be the origin and the line as above. Let be the point ; then is and the equation of the line is . The line through perpendicular to is
:
To find the point of intersection , set in this equation to get
:
which are the parametric equations given above.
While this construction produces arbitrarily many points on the cissoid, it cannot trace any continuous segment of the curve.
 The following construction was given by
The following construction was given by
 Diocles did not really solve the Delian problem. The reason is that the cissoid of Diocles cannot be constructed perfectly, at least not with compass and straightedge. To construct the cissoid of Diocles, one would construct a finite number of its individual points, then connect all these points to form a curve. (An example of this construction is shown on the right.) The problem is that there is no well-defined way to connect the points. If they are connected by line segments, then the construction will be well-defined, but it will not be an exact cissoid of Diocles, but only an approximation. Likewise, if the dots are connected with circular arcs, the construction will be well-defined, but incorrect. Or one could simply draw a curve directly, trying to eyeball the shape of the curve, but the result would only be imprecise guesswork.
Once the finite set of points on the cissoid have been drawn, then line will probably not intersect one of these points exactly, but will pass between them, intersecting the cissoid of Diocles at some point whose exact location has not been constructed, but has only been approximated. An alternative is to keep adding constructed points to the cissoid which get closer and closer to the intersection with line , but the number of steps may very well be infinite, and the Greeks did not recognize approximations as limits of infinite steps (so they were very puzzled by
Diocles did not really solve the Delian problem. The reason is that the cissoid of Diocles cannot be constructed perfectly, at least not with compass and straightedge. To construct the cissoid of Diocles, one would construct a finite number of its individual points, then connect all these points to form a curve. (An example of this construction is shown on the right.) The problem is that there is no well-defined way to connect the points. If they are connected by line segments, then the construction will be well-defined, but it will not be an exact cissoid of Diocles, but only an approximation. Likewise, if the dots are connected with circular arcs, the construction will be well-defined, but incorrect. Or one could simply draw a curve directly, trying to eyeball the shape of the curve, but the result would only be imprecise guesswork.
Once the finite set of points on the cissoid have been drawn, then line will probably not intersect one of these points exactly, but will pass between them, intersecting the cissoid of Diocles at some point whose exact location has not been constructed, but has only been approximated. An alternative is to keep adding constructed points to the cissoid which get closer and closer to the intersection with line , but the number of steps may very well be infinite, and the Greeks did not recognize approximations as limits of infinite steps (so they were very puzzled by
 The
The
"Cissoid of Diocles" at Visual Dictionary Of Special Plane Curves
"Cissoïde de Dioclès ou Cissoïde Droite" at Encyclopédie des Formes Mathématiques Remarquables
(in French)
"The Cissoid" ''An elementary treatise on cubic and quartic curves'' Alfred Barnard Basset (1901) Cambridge pp. 85ff
{{DEFAULTSORT:Cissoid Of Diocles Cubic curves Articles containing proofs Roulettes (curve) Greek mathematics
 In
In geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, the cissoid of Diocles (; named for Diocles) is a cubic plane curve
In mathematics, a cubic plane curve is a plane algebraic curve defined by a cubic equation
:
applied to homogeneous coordinates for the projective plane; or the inhomogeneous version for the affine space determined by setting in such an ...
notable for the property that it can be used to construct two mean proportionals to a given ratio
In mathematics, a ratio () shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
. In particular, it can be used to double a cube. It can be defined as the cissoid
In geometry, a cissoid () is a plane curve generated from two given curves , and a point (the pole). Let be a variable line passing through and intersecting at and at . Let be the point on so that \overline = \overline. (There are actua ...
of a circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
and a line tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points o ...
to it with respect to the point on the circle opposite to the point of tangency. In fact, the curve family of cissoids is named for this example and some authors refer to it simply as ''the'' cissoid. It has a single cusp
A cusp is the most pointed end of a curve. It often refers to cusp (anatomy), a pointed structure on a tooth.
Cusp or CUSP may also refer to:
Mathematics
* Cusp (singularity), a singular point of a curve
* Cusp catastrophe, a branch of bifu ...
at the pole, and is symmetric about the diameter of the circle which is the line of tangency of the cusp. The line is an asymptote
In analytic geometry, an asymptote () of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the ''x'' or ''y'' coordinates tends to infinity. In projective geometry and related contexts, ...
. It is a member of the conchoid of de Sluze
In algebraic geometry, the conchoids of de Sluze are a family of plane curves studied in 1662 by Walloon mathematician René François Walter, baron de Sluze.
The curves are defined by the polar equation
:r=\sec\theta+a\cos\theta \,.
In cartes ...
family of curves and in form it resembles a tractrix
In geometry, a tractrix (; plural: tractrices) is the curve along which an object moves, under the influence of friction, when pulled on a horizontal plane by a line segment attached to a pulling point (the ''tractor'') that moves at a right angl ...
.
Construction and equations
Let the radius of be . By translation and rotation, we may take to be the origin and the center of the circle to be (''a'', 0), so is . Then the polar equations of and are: : By construction, the distance from the origin to a point on the cissoid is equal to the difference between the distances between the origin and the corresponding points on and . In other words, the polar equation of the cissoid is : Applying some trigonometric identities, this is equivalent to : Let in the above equation. Then : are parametric equations for the cissoid. Converting the polar form to Cartesian coordinates produces :Construction by double projection
Newton's construction
Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed ...
. Let be a line and a point not on . Let be a right angle which moves so that equals the distance from to and remains on , while the other leg slides along . Then the midpoint of describes the curve.
To see this, let the distance between and be . By translation and rotation, take and the line . Let and let be the angle between and the -axis; this is equal to the angle between and . By construction, , so the distance from to is . In other words . Also, is the -coordinate of if it is rotated by angle , so . After simplification, this produces parametric equations
:
Change parameters by replacing with its complement to get
:
or, applying double angle formulas,
:
But this is polar equation
:
given above with .
Note that, as with the double projection construction, this can be adapted to produce a mechanical device that generates the curve.
Delian problem
The Greek geometer Diocles used the cissoid to obtain two mean proportionals to a givenratio
In mathematics, a ratio () shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
. This means that given lengths and , the curve can be used to find and so that is to as is to as is to , i.e. , as discovered by Hippocrates of Chios
Hippocrates of Chios (; c. 470 – c. 421 BC) was an ancient Greek mathematician, geometer, and astronomer.
He was born on the isle of Chios, where he was originally a merchant. After some misadventures (he was robbed by either pirates or ...
. As a special case, this can be used to solve the Delian problem: how much must the length of a cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...
be increased in order to double
Double, The Double or Dubble may refer to:
Mathematics and computing
* Multiplication by 2
* Double precision, a floating-point representation of numbers that is typically 64 bits in length
* A double number of the form x+yj, where j^2=+1
* A ...
its volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch) ...
? Specifically, if is the side of a cube, and , then the volume of a cube of side is
:
so is the side of a cube with double the volume of the original cube. Note however that this solution does not fall within the rules of compass and straightedge construction
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an ideali ...
since it relies on the existence of the cissoid.
Let and be given. It is required to find so that , giving and as the mean proportionals. Let the cissoid
:
be constructed as above, with the origin, the point , and the line , also as given above. Let be the point of intersection of with . From the given length , mark on so that . Draw and let be the point where it intersects the cissoid. Draw and let it intersect at . Then is the required length.
To see this, rewrite the equation of the curve as
:
and let , so is the perpendicular to through .
From the equation of the curve,
:
From this,
:
By similar triangles and . So the equation becomes
:
so
:
as required.
 Diocles did not really solve the Delian problem. The reason is that the cissoid of Diocles cannot be constructed perfectly, at least not with compass and straightedge. To construct the cissoid of Diocles, one would construct a finite number of its individual points, then connect all these points to form a curve. (An example of this construction is shown on the right.) The problem is that there is no well-defined way to connect the points. If they are connected by line segments, then the construction will be well-defined, but it will not be an exact cissoid of Diocles, but only an approximation. Likewise, if the dots are connected with circular arcs, the construction will be well-defined, but incorrect. Or one could simply draw a curve directly, trying to eyeball the shape of the curve, but the result would only be imprecise guesswork.
Once the finite set of points on the cissoid have been drawn, then line will probably not intersect one of these points exactly, but will pass between them, intersecting the cissoid of Diocles at some point whose exact location has not been constructed, but has only been approximated. An alternative is to keep adding constructed points to the cissoid which get closer and closer to the intersection with line , but the number of steps may very well be infinite, and the Greeks did not recognize approximations as limits of infinite steps (so they were very puzzled by
Diocles did not really solve the Delian problem. The reason is that the cissoid of Diocles cannot be constructed perfectly, at least not with compass and straightedge. To construct the cissoid of Diocles, one would construct a finite number of its individual points, then connect all these points to form a curve. (An example of this construction is shown on the right.) The problem is that there is no well-defined way to connect the points. If they are connected by line segments, then the construction will be well-defined, but it will not be an exact cissoid of Diocles, but only an approximation. Likewise, if the dots are connected with circular arcs, the construction will be well-defined, but incorrect. Or one could simply draw a curve directly, trying to eyeball the shape of the curve, but the result would only be imprecise guesswork.
Once the finite set of points on the cissoid have been drawn, then line will probably not intersect one of these points exactly, but will pass between them, intersecting the cissoid of Diocles at some point whose exact location has not been constructed, but has only been approximated. An alternative is to keep adding constructed points to the cissoid which get closer and closer to the intersection with line , but the number of steps may very well be infinite, and the Greeks did not recognize approximations as limits of infinite steps (so they were very puzzled by Zeno's paradoxes
Zeno's paradoxes are a series of philosophical arguments presented by the ancient Greek philosopher Zeno of Elea (c. 490–430 BC), primarily known through the works of Plato, Aristotle, and later commentators like Simplicius of Cilicia. Zeno de ...
).
One could also construct a cissoid of Diocles by means of a mechanical tool specially designed for that purpose, but this violates the rule of only using compass and straightedge. This rule was established for reasons of logical — axiomatic — consistency. Allowing construction by new tools would be like adding new axiom
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy or ...
s, but axioms are supposed to be simple and self-evident, but such tools are not. So by the rules of classical, synthetic geometry
Synthetic geometry (sometimes referred to as axiomatic geometry or even pure geometry) is geometry without the use of coordinates. It relies on the axiomatic method for proving all results from a few basic properties initially called postulates ...
, Diocles did not solve the Delian problem, which actually can not be solved by such means.
As a pedal curve
 The
The pedal curve
A pedal (from the Latin ''wikt:pes#Latin, pes'' ''pedis'', "foot") is a lever designed to be operated by foot and may refer to:
Computers and other equipment
* Footmouse, a foot-operated computer mouse
* In medical transcription, a pedal is us ...
of a parabola with respect to its vertex is a cissoid of Diocles. The geometrical properties of pedal curves in general produce several alternate methods of constructing the cissoid. It is the envelopes of circles whose centers lie on a parabola and which pass through the vertex of the parabola. Also, if two congruent parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactl ...
s are set vertex-to-vertex and one is rolled along the other; the vertex of the rolling parabola will trace the cissoid.
Inversion
The cissoid of Diocles can also be defined as theinverse curve
In inversive geometry, an inverse curve of a given curve is the result of applying an inverse operation to . Specifically, with respect to a fixed circle with center and radius the inverse of a point is the point for which lies on the ray ...
of a parabola with the center of inversion at the vertex. To see this, take the parabola to be ''x'' = ''y''2, in polar coordinate or:
:
The inverse curve is thus:
:
which agrees with the polar equation of the cissoid above.
References
* *"Cissoid of Diocles" at Visual Dictionary Of Special Plane Curves
"Cissoïde de Dioclès ou Cissoïde Droite" at Encyclopédie des Formes Mathématiques Remarquables
(in French)
"The Cissoid" ''An elementary treatise on cubic and quartic curves'' Alfred Barnard Basset (1901) Cambridge pp. 85ff
{{DEFAULTSORT:Cissoid Of Diocles Cubic curves Articles containing proofs Roulettes (curve) Greek mathematics