Chinese mathematics on:
[Wikipedia]
[Google]
[Amazon]
Mathematics emerged independently in China by the 11th century BCE. The Chinese independently developed a







 In the third century
In the third century 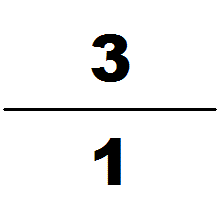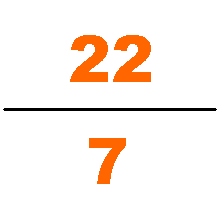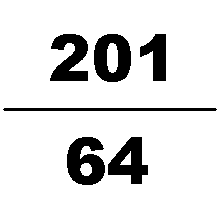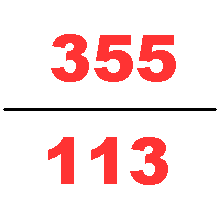 In the fourth century, another influential mathematician named Zu Chongzhi, introduced the ''Da Ming Li.'' This calendar was specifically calculated to predict many cosmological cycles that will occur in a period of time. Very little is really known about his life. Today, the only sources are found in Book of Sui, we now know that Zu Chongzhi was one of the generations of mathematicians. He used Liu Hui's pi-algorithm applied to a 12288-gon and obtained a value of pi to 7 accurate decimal places (between 3.1415926 and 3.1415927), which would remain the most accurate approximation of π available for the next 900 years. He also applied He Chengtian's interpolation for approximating irrational number with fraction in his astronomy and mathematical works, he obtained as a good fraction approximate for pi; Yoshio Mikami commented that neither the Greeks, nor the Hindus nor Arabs knew about this fraction approximation to pi, not until the Dutch mathematician Adrian Anthoniszoom rediscovered it in 1585, "the Chinese had therefore been possessed of this the most extraordinary of all fractional values over a whole millennium earlier than Europe".
Along with his son, Zu Geng, Zu Chongzhi applied the Cavalieri's principle to find an accurate solution for calculating the volume of the sphere. Besides containing formulas for the volume of the sphere, his book also included formulas of cubic equations and the accurate value of pi. His work, ''Zhui Shu'' was discarded out of the syllabus of mathematics during the Song dynasty and lost. Many believed that ''Zhui Shu'' contains the formulas and methods for
In the fourth century, another influential mathematician named Zu Chongzhi, introduced the ''Da Ming Li.'' This calendar was specifically calculated to predict many cosmological cycles that will occur in a period of time. Very little is really known about his life. Today, the only sources are found in Book of Sui, we now know that Zu Chongzhi was one of the generations of mathematicians. He used Liu Hui's pi-algorithm applied to a 12288-gon and obtained a value of pi to 7 accurate decimal places (between 3.1415926 and 3.1415927), which would remain the most accurate approximation of π available for the next 900 years. He also applied He Chengtian's interpolation for approximating irrational number with fraction in his astronomy and mathematical works, he obtained as a good fraction approximate for pi; Yoshio Mikami commented that neither the Greeks, nor the Hindus nor Arabs knew about this fraction approximation to pi, not until the Dutch mathematician Adrian Anthoniszoom rediscovered it in 1585, "the Chinese had therefore been possessed of this the most extraordinary of all fractional values over a whole millennium earlier than Europe".
Along with his son, Zu Geng, Zu Chongzhi applied the Cavalieri's principle to find an accurate solution for calculating the volume of the sphere. Besides containing formulas for the volume of the sphere, his book also included formulas of cubic equations and the accurate value of pi. His work, ''Zhui Shu'' was discarded out of the syllabus of mathematics during the Song dynasty and lost. Many believed that ''Zhui Shu'' contains the formulas and methods for
 Four outstanding mathematicians arose during the
Four outstanding mathematicians arose during the
 The '' Jade Mirror of the Four Unknowns'' was written by Zhu Shijie in 1303 AD and marks the peak in the development of Chinese algebra. The four elements, called heaven, earth, man and matter, represented the four unknown quantities in his algebraic equations. It deals with simultaneous equations and with equations of degrees as high as fourteen. The author uses the method of ''fan fa'', today called Horner's method, to solve these equations.
There are many summation series equations given without proof in the ''Mirror''. A few of the summation series are:
The '' Jade Mirror of the Four Unknowns'' was written by Zhu Shijie in 1303 AD and marks the peak in the development of Chinese algebra. The four elements, called heaven, earth, man and matter, represented the four unknown quantities in his algebraic equations. It deals with simultaneous equations and with equations of degrees as high as fourteen. The author uses the method of ''fan fa'', today called Horner's method, to solve these equations.
There are many summation series equations given without proof in the ''Mirror''. A few of the summation series are:
 Instead, mathematical progress became focused on computational tools. In 15 century, abacus came into its ''suan pan'' form. Easy to use and carry, both fast and accurate, it rapidly overtook rod calculus as the preferred form of computation. ''Zhusuan'', the arithmetic calculation through abacus, inspired multiple new works. ''Suanfa Tongzong'' (General Source of Computational Methods), a 17-volume work published in 1592 by Cheng Dawei, remained in use for over 300 years. Zhu Zaiyu, Prince of Zheng used 81 position abacus to calculate the square root and cubic root of 2 to 25 figure accuracy, a precision that enabled his development of the equal-temperament system.
In the late 16th century, Matteo Ricci decided to published Western scientific works in order to establish a position at the Imperial Court. With the assistance of Xu Guangqi, he was able to translate Euclid's ''Elements'' using the same techniques used to teach classical Buddhist texts. Other missionaries followed in his example, translating Western works on special functions (trigonometry and logarithms) that were neglected in the Chinese tradition. However, contemporary scholars found the emphasis on proofs — as opposed to solved problems — baffling, and most continued to work from classical texts alone.
Instead, mathematical progress became focused on computational tools. In 15 century, abacus came into its ''suan pan'' form. Easy to use and carry, both fast and accurate, it rapidly overtook rod calculus as the preferred form of computation. ''Zhusuan'', the arithmetic calculation through abacus, inspired multiple new works. ''Suanfa Tongzong'' (General Source of Computational Methods), a 17-volume work published in 1592 by Cheng Dawei, remained in use for over 300 years. Zhu Zaiyu, Prince of Zheng used 81 position abacus to calculate the square root and cubic root of 2 to 25 figure accuracy, a precision that enabled his development of the equal-temperament system.
In the late 16th century, Matteo Ricci decided to published Western scientific works in order to establish a position at the Imperial Court. With the assistance of Xu Guangqi, he was able to translate Euclid's ''Elements'' using the same techniques used to teach classical Buddhist texts. Other missionaries followed in his example, translating Western works on special functions (trigonometry and logarithms) that were neglected in the Chinese tradition. However, contemporary scholars found the emphasis on proofs — as opposed to solved problems — baffling, and most continued to work from classical texts alone.
Early mathematics texts
(Chinese) - Chinese Text Project
Overview of Chinese mathematics
Primer of Mathematics
by Zhu Shijie {{DEFAULTSORT:Chinese mathematics Chinese mathematics,
real number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every re ...
system that includes significantly large and negative number
In mathematics, a negative number is the opposite (mathematics), opposite of a positive real number. Equivalently, a negative number is a real number that is inequality (mathematics), less than 0, zero. Negative numbers are often used to represe ...
s, more than one numeral system
A numeral system is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner.
The same sequence of symbols may represent differe ...
( binary and decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers (''decimal fractions'') of th ...
), algebra
Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic ope ...
, geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example ...
and trigonometry
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The fiel ...
.
Since the Han dynasty
The Han dynasty was an Dynasties of China, imperial dynasty of China (202 BC9 AD, 25–220 AD) established by Liu Bang and ruled by the House of Liu. The dynasty was preceded by the short-lived Qin dynasty (221–206 BC ...
, as diophantine approximation
In number theory, the study of Diophantine approximation deals with the approximation of real numbers by rational numbers. It is named after Diophantus of Alexandria.
The first problem was to know how well a real number can be approximated ...
being a prominent numerical method
In numerical analysis, a numerical method is a mathematical tool designed to solve numerical problems. The implementation of a numerical method with an appropriate convergence check in a programming language is called a numerical algorithm.
Mathem ...
, the Chinese made substantial progress on polynomial evaluation. Algorithms like regula falsi and expressions like simple continued fraction
A simple or regular continued fraction is a continued fraction with numerators all equal one, and denominators built from a sequence \ of integer numbers. The sequence can be finite or infinite, resulting in a finite (or terminated) continued fr ...
s are widely used and have been well-documented ever since. They deliberately find the principal ''n''th root of positive numbers and the roots of equations. The major texts from the period, '' The Nine Chapters on the Mathematical Art'' and the '' Book on Numbers and Computation'' gave detailed processes for solving various mathematical problems in daily life. All procedures were computed using a counting board in both texts, and they included inverse element
In mathematics, the concept of an inverse element generalises the concepts of opposite () and reciprocal () of numbers.
Given an operation denoted here , and an identity element denoted , if , one says that is a left inverse of , and that ...
s as well as Euclidean division
In arithmetic, Euclidean division – or division with remainder – is the process of dividing one integer (the dividend) by another (the divisor), in a way that produces an integer quotient and a natural number remainder strictly smaller than ...
s. The texts provide procedures similar to that of Gaussian elimination
In mathematics, Gaussian elimination, also known as row reduction, is an algorithm for solving systems of linear equations. It consists of a sequence of row-wise operations performed on the corresponding matrix of coefficients. This method can a ...
and Horner's method for linear algebra
Linear algebra is the branch of mathematics concerning linear equations such as
:a_1x_1+\cdots +a_nx_n=b,
linear maps such as
:(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n,
and their representations in vector spaces and through matrix (mathemat ...
. The achievement of Chinese algebra reached a zenith in the 13th century during the Yuan dynasty
The Yuan dynasty ( ; zh, c=元朝, p=Yuáncháo), officially the Great Yuan (; Mongolian language, Mongolian: , , literally 'Great Yuan State'), was a Mongol-led imperial dynasty of China and a successor state to the Mongol Empire after Div ...
with the development of ''tian yuan shu
''Tian yuan shu'' () is a Chinese system of algebra for polynomial equations. Some of the earliest existing writings were created in the 13th century during the Yuan dynasty. However, the tianyuanshu method was known much earlier, in the Song dy ...
''.
As a result of obvious linguistic and geographic barriers, as well as content, Chinese mathematics and the mathematics of the ancient Mediterranean world are presumed to have developed more or less independently up to the time when ''The Nine Chapters on the Mathematical Art'' reached its final form, while the ''Book on Numbers and Computation'' and ''Huainanzi
The ''Huainanzi'' is an ancient Chinese text made up of essays from scholarly debates held at the court of Liu An, Prince of Huainan, before 139 BCE. Compiled as a handbook for an enlightened sovereign and his court, the work attempts to defi ...
'' are roughly contemporary with classical Greek mathematics. Some exchange of ideas across Asia through known cultural exchanges from at least Roman times is likely. Frequently, elements of the mathematics of early societies correspond to rudimentary results found later in branches of modern mathematics such as geometry or number theory. The Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
for example, has been attested to the time of the Duke of Zhou
Dan, Duke Wen of Zhou, commonly known as the Duke of Zhou, was a member of the royal family of the early Zhou dynasty who played a major role in consolidating the kingdom established by his elder brother King Wu. He was renowned for acting as ...
. Knowledge of Pascal's triangle
In mathematics, Pascal's triangle is an infinite triangular array of the binomial coefficients which play a crucial role in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Bla ...
has also been shown to have existed in China centuries before Pascal, such as the Song-era polymath Shen Kuo
Shen Kuo (; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and Art name#China, pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁),Yao (2003), 544. was a Chinese polymath, scientist, and statesman of the Song dynasty (960� ...
.
Pre-imperial era


Shang dynasty
The Shang dynasty (), also known as the Yin dynasty (), was a Chinese royal dynasty that ruled in the Yellow River valley during the second millennium BC, traditionally succeeding the Xia dynasty and followed by the Western Zhou d ...
(1600–1050 BC). One of the oldest surviving mathematical works is the ''I Ching
The ''I Ching'' or ''Yijing'' ( ), usually translated ''Book of Changes'' or ''Classic of Changes'', is an ancient Chinese divination text that is among the oldest of the Chinese classics. The ''I Ching'' was originally a divination manual in ...
'', which greatly influenced written literature during the Zhou dynasty
The Zhou dynasty ( ) was a royal dynasty of China that existed for 789 years from until 256 BC, the longest span of any dynasty in Chinese history. During the Western Zhou period (771 BC), the royal house, surnamed Ji, had military ...
(1050–256 BC). For mathematics, the book included a sophisticated use of hexagram
, can be seen as a compound polygon, compound composed of an upwards (blue here) and downwards (pink) facing equilateral triangle, with their intersection as a regular hexagon (in green).
A hexagram (Greek language, Greek) or sexagram (Latin l ...
s. Leibniz pointed out, the I Ching (Yi Jing) contained elements of binary number
A binary number is a number expressed in the Radix, base-2 numeral system or binary numeral system, a method for representing numbers that uses only two symbols for the natural numbers: typically "0" (zero) and "1" (one). A ''binary number'' may ...
s.
Since the Shang period, the Chinese had already fully developed a decimal system. Since early times, Chinese understood basic arithmetic
Arithmetic is an elementary branch of mathematics that deals with numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms.
...
(which dominated far eastern history), algebra, equations, and negative numbers with counting rods
Counting rods (筭) are small bars, typically 3–14 cm (1" to 6") long, that were used by mathematicians for calculation in ancient East Asia. They are placed either horizontally or vertically to represent any integer or rational number.
...
. Although the Chinese were more focused on arithmetic and advanced algebra for astronomical
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest include ...
uses, they were also the first to develop negative numbers, algebraic geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; th ...
, and the usage of decimals.
Math was one of the Six Arts students were required to master during the Zhou dynasty
The Zhou dynasty ( ) was a royal dynasty of China that existed for 789 years from until 256 BC, the longest span of any dynasty in Chinese history. During the Western Zhou period (771 BC), the royal house, surnamed Ji, had military ...
(1122–256 BCE). Learning them all perfectly was required to be a perfect gentleman, comparable to the concept of a " renaissance man". Six Arts have their roots in the Confucian philosophy.
The oldest existent work on geometry in China comes from the philosophical Mohist canon , compiled by the followers of Mozi (470–390 BCE). The ''Mo Jing'' described various aspects of many fields associated with physical science, and provided a small wealth of information on mathematics as well. It provided an 'atomic' definition of the geometric point, stating that a line is separated into parts, and the part which has no remaining parts (i.e. cannot be divided into smaller parts) and thus forms the extreme end of a line is a point. Much like Euclid
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely domina ...
's first and third definitions and Plato
Plato ( ; Greek language, Greek: , ; born BC, died 348/347 BC) was an ancient Greek philosopher of the Classical Greece, Classical period who is considered a foundational thinker in Western philosophy and an innovator of the writte ...
's 'beginning of a line', the ''Mo Jing'' stated that "a point may stand at the end (of a line) or at its beginning like a head-presentation in childbirth. (As to its invisibility) there is nothing similar to it." Similar to the atomists of Democritus
Democritus (, ; , ''Dēmókritos'', meaning "chosen of the people"; – ) was an Ancient Greece, Ancient Greek Pre-Socratic philosophy, pre-Socratic philosopher from Abdera, Thrace, Abdera, primarily remembered today for his formulation of an ...
, the ''Mo Jing'' stated that a point is the smallest unit, and cannot be cut in half, since 'nothing' cannot be halved." It stated that two lines of equal length will always finish at the same place," while providing definitions for the ''comparison of lengths'' and for ''parallels''," along with principles of space and bounded space. It also described the fact that planes without the quality of thickness cannot be piled up since they cannot mutually touch. The book provided word recognition for circumference, diameter, and radius, along with the definition of volume.
The history of mathematical development lacks some evidence. There are still debates about certain mathematical classics. For example, the ''Zhoubi Suanjing
The ''Zhoubi Suanjing'', also known by many other names, is an ancient Chinese astronomical and mathematical work. The ''Zhoubi'' is most famous for its presentation of Chinese cosmology and a form of the Pythagorean theorem. It claims to pr ...
'' dates around 1200–1000 BC, yet many scholars believed it was written between 300 and 250 BCE. The ''Zhoubi Suanjing'' contains an in-depth proof of the ''Gougu Theorem'' (a special case of the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
), but focuses more on astronomical calculations. However, the recent archaeological discovery of the Tsinghua Bamboo Slips, dated , has revealed some aspects of pre-Qin mathematics, such as the first known decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers (''decimal fractions'') of th ...
multiplication table.
The abacus
An abacus ( abaci or abacuses), also called a counting frame, is a hand-operated calculating tool which was used from ancient times in the ancient Near East, Europe, China, and Russia, until the adoption of the Hindu–Arabic numeral system. A ...
was first mentioned in the second century BC, alongside 'calculation with rods' (''suan zi'') in which small bamboo sticks are placed in successive squares of a checkerboard.
Qin dynasty
Not much is known aboutQin dynasty
The Qin dynasty ( ) was the first Dynasties of China, imperial dynasty of China. It is named for its progenitor state of Qin, a fief of the confederal Zhou dynasty (256 BC). Beginning in 230 BC, the Qin under King Ying Zheng enga ...
mathematics, or before, due to the burning of books and burying of scholars
The burning of books and burying of scholars was the purported Book burning, burning of texts in 213 BCE and live burial of 460 Confucian scholars in 212 BCE ordered by Chinese emperor Qin Shi Huang. The events were alleged to have destroye ...
, circa 213–210 BC. Knowledge of this period can be determined from civil projects and historical evidence. The Qin dynasty created a standard system of weights. Civil projects of the Qin dynasty were significant feats of human engineering. Emperor Qin Shi Huang
Qin Shi Huang (, ; February 25912 July 210 BC), born Ying Zheng () or Zhao Zheng (), was the founder of the Qin dynasty and the first emperor of China. He is widely regarded as the first ever supreme leader of a unitary state, unitary d ...
ordered many men to build large, life-sized statues for the palace tomb along with other temples and shrines, and the shape of the tomb was designed with geometric skills of architecture. It is certain that one of the greatest feats of human history, the Great Wall of China
The Great Wall of China (, literally "ten thousand ''li'' long wall") is a series of fortifications in China. They were built across the historical northern borders of ancient Chinese states and Imperial China as protection against vario ...
, required many mathematical techniques. All Qin dynasty buildings and grand projects used advanced computation formulas for volume, area and proportion.
Qin bamboo cash purchased at the antiquarian market of Hong Kong
Hong Kong)., Legally Hong Kong, China in international treaties and organizations. is a special administrative region of China. With 7.5 million residents in a territory, Hong Kong is the fourth most densely populated region in the wor ...
by the Yuelu Academy, according to the preliminary reports, contains the earliest epigraphic sample of a mathematical treatise.
Han dynasty
In the Han dynasty, numbers were developed into a place value decimal system and used on a counting board with a set ofcounting rods
Counting rods (筭) are small bars, typically 3–14 cm (1" to 6") long, that were used by mathematicians for calculation in ancient East Asia. They are placed either horizontally or vertically to represent any integer or rational number.
...
called rod calculus, consisting of only nine symbols with a blank space on the counting board representing zero. Negative numbers and fractions were also incorporated into solutions of the great mathematical texts of the period. The mathematical texts of the time, the '' Book on Numbers and Computation'' and '' Jiuzhang suanshu'' solved basic arithmetic problems such as addition, subtraction, multiplication and division. Furthermore, they gave the processes for square and cubed root extraction, which eventually was applied to solving quadratic equations up to the third order. Both texts also made substantial progress in Linear Algebra, namely solving systems of equations with multiple unknowns. The value of pi is taken to be equal to three in both texts. However, the mathematicians Liu Xin (d. 23) and Zhang Heng
Zhang Heng (; AD 78–139), formerly romanization of Chinese, romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Han dynasty#Eastern Han (25–220 AD), Eastern Han dynasty. Educated in the capital citi ...
(78–139) gave more accurate approximations for pi than Chinese of previous centuries had used. Mathematics was developed to solve practical problems in the time such as division of land or problems related to division of payment. The Chinese did not focus on theoretical proofs based on geometry or algebra in the modern sense of proving equations to find area or volume. The Book of Computations and The Nine Chapters on the Mathematical Art provide numerous practical examples that would be used in daily life.
''Book on Numbers and Computation''
The '' Book on Numbers and Computation'' is approximately seven thousand characters in length, written on 190 bamboo strips. It was discovered together with other writings in 1984 whenarchaeologist
Archaeology or archeology is the study of human activity through the recovery and analysis of material culture. The archaeological record consists of Artifact (archaeology), artifacts, architecture, biofact (archaeology), biofacts or ecofacts, ...
s opened a tomb at Zhangjiashan in Hubei
Hubei is a province of China, province in Central China. It has the List of Chinese provincial-level divisions by GDP, seventh-largest economy among Chinese provinces, the second-largest within Central China, and the third-largest among inland ...
province. From documentary evidence this tomb is known to have been closed in 186 BC, early in the Western Han dynasty
The Han dynasty was an Dynasties of China, imperial dynasty of China (202 BC9 AD, 25–220 AD) established by Liu Bang and ruled by the House of Liu. The dynasty was preceded by the short-lived Qin dynasty (221–206 BC ...
. While its relationship to the Nine Chapters is still under discussion by scholars, some of its contents are clearly paralleled there. The text of the ''Suan shu shu'' is however much less systematic than the Nine Chapters, and appears to consist of a number of more or less independent short sections of text drawn from a number of sources.
The Book of Computations contains many perquisites to problems that would be expanded upon in The Nine Chapters on the Mathematical Art. An example of the elementary mathematics in the ''Suàn shù shū'', the square root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4 ...
is approximated by using false position method which says to "combine the excess and deficiency as the divisor; (taking) the deficiency numerator multiplied by the excess denominator and the excess numerator times the deficiency denominator, combine them as the dividend." Furthermore, The Book of Computations solves systems of two equations and two unknowns using the same false position method.
''The Nine Chapters on the Mathematical Art''
'' The Nine Chapters on the Mathematical Art'' dates archeologically to 179 CE, though it is traditionally dated to 1000 BCE, but it was written perhaps as early as 300–200 BCE. Although the author(s) are unknown, they made a major contribution in the eastern world. Problems are set up with questions immediately followed by answers and procedure. There are no formal mathematical proofs within the text, just a step-by-step procedure. The commentary of Liu Hui provided geometrical and algebraic proofs to the problems given within the text. ''The Nine Chapters on the Mathematical Art'' was one of the most influential of all Chinese mathematical books and it is composed of 246 problems. It was later incorporated into ''The Ten Computational Canons'', which became the core of mathematical education in later centuries. This book includes 246 problems on surveying, agriculture, partnerships, engineering, taxation, calculation, the solution of equations, and the properties of right triangles. ''The Nine Chapters'' made significant additions to solving quadratic equations in a way similar to Horner's method. It also made advanced contributions to ''fangcheng'', or what is now known as linear algebra. Chapter seven solvessystem of linear equations
In mathematics, a system of linear equations (or linear system) is a collection of two or more linear equations involving the same variable (math), variables.
For example,
: \begin
3x+2y-z=1\\
2x-2y+4z=-2\\
-x+\fracy-z=0
\end
is a system of th ...
with two unknowns using the false position method, similar to The Book of Computations. Chapter eight deals with solving determinate and indeterminate simultaneous linear equations using positive and negative numbers, with one problem dealing with solving four equations in five unknowns. The Nine Chapters solves systems of equations using methods similar to the modern Gaussian elimination
In mathematics, Gaussian elimination, also known as row reduction, is an algorithm for solving systems of linear equations. It consists of a sequence of row-wise operations performed on the corresponding matrix of coefficients. This method can a ...
and back substitution.
The version of ''The Nine Chapters'' that has served as the foundation for modern renditions was a result of the efforts of the scholar Dai Zhen. Transcribing the problems directly from ''Yongle Encyclopedia'', he then proceeded to make revisions to the original text, along with the inclusion his own notes explaining his reasoning behind the alterations. His finished work would be first published in 1774, but a new revision would be published in 1776 to correct various errors as well as include a version of ''The Nine Chapters'' from the Southern Song that contained the commentaries of Lui Hui and Li Chunfeng. The final version of Dai Zhen's work would come in 1777, titled ''Ripple Pavilion'', with this final rendition being widely distributed and coming to serve as the standard for modern versions of ''The Nine Chapters''. However, this version has come under scrutiny from Guo Shuchen, alleging that the edited version still contains numerous errors and that not all of the original amendments were done by Dai Zhen himself.
Calculation of pi
Problems in The Nine Chapters on the Mathematical Art take pi to be equal to three in calculating problems related to circles and spheres, such as spherical surface area. There is no explicit formula given within the text for the calculation of pi to be three, but it is used throughout the problems of both The Nine Chapters on the Mathematical Art and the Artificer's Record, which was produced in the same time period. Historians believe that this figure of pi was calculated using the 3:1 relationship between the circumference and diameter of a circle. Some Han mathematicians attempted to improve this number, such as Liu Xin, who is believed to have estimated pi to be 3.154. Later, Liu Hui attempted to improve the calculation by calculating pi to be 3.141024. Liu calculated this number by using polygons inside a hexagon as a lower limit compared to a circle. Zu Chongzhi later discovered the calculation of pi to be 3.1415926 < π < 3.1415927 by using polygons with 24,576 sides. This calculation would be discovered in Europe during the 16th century. There is no explicit method or record of how he calculated this estimate.Division and root extraction
Basic arithmetic processes such as addition, subtraction, multiplication and division were present before the Han dynasty. ''The Nine Chapters on the Mathematical Art'' take these basic operations for granted and simply instruct the reader to perform them. Han mathematicians calculated square and cube roots in a similar manner as division, and problems on division and root extraction both occur in Chapter Four of ''The Nine Chapters on the Mathematical Art''. Calculating the square and cube roots of numbers is done through successive approximation, the same as division, and often uses similar terms such as dividend (''shi'') and divisor (''fa'') throughout the process. This process of successive approximation was then extended to solving quadratics of the second and third order, such as , using a method similar to Horner's method. The method was not extended to solve quadratics of the nth order during the Han dynasty; however, this method was eventually used to solve these equations.Linear algebra
''The Book of Computations'' is the first known text to solve systems of equations with two unknowns. There are a total of three sets of problems within ''The Book of Computations'' involving solving systems of equations with the false position method, which again are put into practical terms. Chapter Seven of ''The Nine Chapters on the Mathematical Art'' also deals with solving a system of two equations with two unknowns with the false position method. To solve for the greater of the two unknowns, the false position method instructs the reader to cross-multiply the minor terms or ''zi'' (which are the values given for the excess and deficit) with the major terms ''mu''. To solve for the lesser of the two unknowns, simply add the minor terms together. Chapter Eight of ''The Nine Chapters on the Mathematical Art'' deals with solving infinite equations with infinite unknowns. This process is referred to as the "fangcheng procedure" throughout the chapter. Many historians chose to leave the term ''fangcheng'' untranslated due to conflicting evidence of what the term means. Many historians translate the word tolinear algebra
Linear algebra is the branch of mathematics concerning linear equations such as
:a_1x_1+\cdots +a_nx_n=b,
linear maps such as
:(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n,
and their representations in vector spaces and through matrix (mathemat ...
today. In this chapter, the process of Gaussian elimination and back-substitution are used to solve systems of equations with many unknowns. Problems were done on a counting board and included the use of negative numbers as well as fractions. The counting board was effectively a matrix
Matrix (: matrices or matrixes) or MATRIX may refer to:
Science and mathematics
* Matrix (mathematics), a rectangular array of numbers, symbols or expressions
* Matrix (logic), part of a formula in prenex normal form
* Matrix (biology), the m ...
, where the top line is the first variable of one equation and the bottom was the last.
Liu Hui's commentary on ''The Nine Chapters on the Mathematical Art''
Liu Hui
Liu Hui () was a Chinese mathematician who published a commentary in 263 CE on ''Jiu Zhang Suan Shu ( The Nine Chapters on the Mathematical Art).'' He was a descendant of the Marquis of Zixiang of the Eastern Han dynasty and lived in the state ...
's commentary on ''The Nine Chapters on the Mathematical Art'' is the earliest edition of the original text available. Hui is believed by most to be a mathematician shortly after the Han dynasty. Within his commentary, Hui qualified and proved some of the problems from either an algebraic or geometrical standpoint. For instance, throughout ''The Nine Chapters on the Mathematical Art'', the value of pi is taken to be equal to three in problems regarding circles or spheres. In his commentary, Liu Hui finds a more accurate estimation of pi using the method of exhaustion
The method of exhaustion () is a method of finding the area of a shape by inscribing inside it a sequence of polygons (one at a time) whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the differ ...
. The method involves creating successive polygons within a circle so that eventually the area of a higher-order polygon will be identical to that of the circle. From this method, Liu Hui asserted that the value of pi is about 3.14. Liu Hui also presented a geometric proof of square and cubed root extraction similar to the Greek method, which involved cutting a square or cube in any line or section and determining the square root through symmetry of the remaining rectangles.
Three Kingdoms, Jin, and Sixteen Kingdoms

 In the third century
In the third century Liu Hui
Liu Hui () was a Chinese mathematician who published a commentary in 263 CE on ''Jiu Zhang Suan Shu ( The Nine Chapters on the Mathematical Art).'' He was a descendant of the Marquis of Zixiang of the Eastern Han dynasty and lived in the state ...
wrote his commentary on the Nine Chapters and also wrote Haidao Suanjing which dealt with using Pythagorean theorem (already known by the 9 chapters), and triple, quadruple triangulation for surveying; his accomplishment in the mathematical surveying exceeded those accomplished in the west by a millennium. He was the first Chinese mathematician to calculate ''π''=3.1416 with his ''π'' algorithm. He discovered the usage of Cavalieri's principle to find an accurate formula for the volume of a cylinder, and also developed elements of the infinitesimal calculus
Calculus is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the calculus of ...
during the 3rd century CE.
linear
In mathematics, the term ''linear'' is used in two distinct senses for two different properties:
* linearity of a '' function'' (or '' mapping'');
* linearity of a '' polynomial''.
An example of a linear function is the function defined by f(x) ...
, matrix algebra, algorithm for calculating the value of ''π'', formula for the volume of the sphere. The text should also associate with his astronomical methods of interpolation, which would contain knowledge, similar to our modern mathematics.
A mathematical manual called ''Sunzi mathematical classic'' dated between 200 and 400 CE contained the most detailed step by step description of multiplication
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division (mathematics), division. The result of a multiplication operation is called a ''Product (mathem ...
and division algorithm with counting rods. Intriguingly, ''Sunzi'' may have influenced the development of place-value systems and place-value systems and the associated Galley division in the West. European sources learned place-value techniques in the 13th century, from a Latin translation an early-9th-century work by Al-Khwarizmi
Muhammad ibn Musa al-Khwarizmi , or simply al-Khwarizmi, was a mathematician active during the Islamic Golden Age, who produced Arabic-language works in mathematics, astronomy, and geography. Around 820, he worked at the House of Wisdom in B ...
. Khwarizmi's presentation is almost identical to the division algorithm in ''Sunzi'', even regarding stylistic matters (for example, using blank spaces to represent trailing zeros); the similarity suggests that the results may not have been an independent discovery. Islamic commentators on Al-Khwarizmi's work believed that it primarily summarized Hindu knowledge; Al-Khwarizmi's failure to cite his sources makes it difficult to determine whether those sources had in turn learned the procedure from China.
In the fifth century the manual called " Zhang Qiujian suanjing" discussed linear and quadratic equations. By this point the Chinese had the concept of negative numbers.
Tang dynasty
By theTang dynasty
The Tang dynasty (, ; zh, c=唐朝), or the Tang Empire, was an Dynasties of China, imperial dynasty of China that ruled from 618 to 907, with an Wu Zhou, interregnum between 690 and 705. It was preceded by the Sui dynasty and followed ...
study of mathematics was fairly standard in the great schools. The Ten Computational Canons was a collection of ten Chinese mathematical works, compiled by early Tang dynasty mathematician Li Chunfeng (李淳風 602–670), as the official mathematical texts for imperial examinations in mathematics. The Sui dynasty
The Sui dynasty ( ) was a short-lived Dynasties of China, Chinese imperial dynasty that ruled from 581 to 618. The re-unification of China proper under the Sui brought the Northern and Southern dynasties era to a close, ending a prolonged peri ...
and Tang dynasty ran the "School of Computations".
Wang Xiaotong was a great mathematician in the beginning of the Tang dynasty
The Tang dynasty (, ; zh, c=唐朝), or the Tang Empire, was an Dynasties of China, imperial dynasty of China that ruled from 618 to 907, with an Wu Zhou, interregnum between 690 and 705. It was preceded by the Sui dynasty and followed ...
, and he wrote a book: Jigu Suanjing (''Continuation of Ancient Mathematics''), where numerical solutions which general cubic equations appear for the first time.
The Tibetans obtained their first knowledge of mathematics (arithmetic) from China during the reign of Nam-ri srong btsan, who died in 630.
The table of sines by the Indian mathematician, Aryabhata
Aryabhata ( ISO: ) or Aryabhata I (476–550 CE) was the first of the major mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy. His works include the '' Āryabhaṭīya'' (which mentions that in 3600 ' ...
, were translated into the Chinese mathematical book of the '' Kaiyuan Zhanjing'', compiled in 718 AD during the Tang dynasty. Although the Chinese excelled in other fields of mathematics such as solid geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, binomial theorem
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, the power expands into a polynomial with terms of the form , where the exponents and a ...
, and complex algebraic formulas, early forms of trigonometry
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The fiel ...
were not as widely appreciated as in the contemporary Indian and Islamic mathematics.
Yi Xing
Yixing (, 683–727) was a Buddhist monk of the Tang dynasty, recognized for his accomplishments as an astronomer, a reformer of the calendar system, a specialist in the ''I Ching, Yijing'' (易經), and a distinguished Buddhist figure with exp ...
, the mathematician and Buddhist monk was credited for calculating the tangent table. Instead, the early Chinese used an empirical
Empirical evidence is evidence obtained through sense experience or experimental procedure. It is of central importance to the sciences and plays a role in various other fields, like epistemology and law.
There is no general agreement on how t ...
substitute known as ''chong cha'', while practical use of plane trigonometry in using the sine, the tangent, and the secant were known. Yi Xing was famed for his genius, and was known to have calculated the number of possible positions on a go board game (though without a symbol for zero he had difficulties expressing the number).
Song and Yuan dynasties
Northern Song dynasty
The Song dynasty ( ) was an imperial dynasty of China that ruled from 960 to 1279. The dynasty was founded by Emperor Taizu of Song, who usurped the throne of the Later Zhou dynasty and went on to conquer the rest of the Ten Kingdoms, endin ...
mathematician Jia Xian developed an additive multiplicative method for extraction of square root and cubic root which implemented the "Horner" rule.
 Four outstanding mathematicians arose during the
Four outstanding mathematicians arose during the Song dynasty
The Song dynasty ( ) was an Dynasties of China, imperial dynasty of China that ruled from 960 to 1279. The dynasty was founded by Emperor Taizu of Song, who usurped the throne of the Later Zhou dynasty and went on to conquer the rest of the Fiv ...
and Yuan dynasty
The Yuan dynasty ( ; zh, c=元朝, p=Yuáncháo), officially the Great Yuan (; Mongolian language, Mongolian: , , literally 'Great Yuan State'), was a Mongol-led imperial dynasty of China and a successor state to the Mongol Empire after Div ...
, particularly in the twelfth and thirteenth centuries: Yang Hui, Qin Jiushao
Qin Jiushao (, ca. 1202–1261), courtesy name Daogu (道古), was a Chinese mathematician, meteorologist, inventor, politician, and writer. He is credited for discovering Horner's method as well as inventing Tianchi basins, a type of rain gau ...
, Li Zhi (Li Ye), and Zhu Shijie. Yang Hui, Qin Jiushao, Zhu Shijie all used the Horner- Ruffini method six hundred years earlier to solve certain types of simultaneous equations, roots, quadratic, cubic, and quartic equations. Yang Hui was also the first person in history to discover and prove "Pascal's Triangle
In mathematics, Pascal's triangle is an infinite triangular array of the binomial coefficients which play a crucial role in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Bla ...
", along with its binomial proof (although the earliest mention of the Pascal's triangle in China exists before the eleventh century AD). Li Zhi on the other hand, investigated on a form of algebraic geometry based on tiān yuán shù. His book; Ceyuan haijing revolutionized the idea of inscribing a circle into triangles, by turning this geometry problem by algebra instead of the traditional method of using Pythagorean theorem. Guo Shoujing of this era also worked on spherical trigonometry for precise astronomical calculations. At this point of mathematical history, a lot of modern western mathematics were already discovered by Chinese mathematicians. Things grew quiet for a time until the thirteenth century Renaissance of Chinese math. This saw Chinese mathematicians solving equations with methods Europe would not know until the eighteenth century. The high point of this era came with Zhu Shijie's two books '' Suanxue qimeng'' and the '' Jade Mirror of the Four Unknowns''. In one case he reportedly gave a method equivalent to Gauss
Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, Geodesy, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observat ...
's pivotal condensation.
Qin Jiushao
Qin Jiushao (, ca. 1202–1261), courtesy name Daogu (道古), was a Chinese mathematician, meteorologist, inventor, politician, and writer. He is credited for discovering Horner's method as well as inventing Tianchi basins, a type of rain gau ...
(1261) was the first to introduce the zero symbol into Chinese mathematics." Before this innovation, blank spaces were used instead of zeros in the system of counting rods
Counting rods (筭) are small bars, typically 3–14 cm (1" to 6") long, that were used by mathematicians for calculation in ancient East Asia. They are placed either horizontally or vertically to represent any integer or rational number.
...
. One of the most important contribution of Qin Jiushao was his method of solving high order numerical equations. Referring to Qin's solution of a 4th order equation, Yoshio Mikami put it: "Who can deny the fact of Horner's illustrious process being used in China at least nearly six long centuries earlier than in Europe?" Qin also solved a 10th order equation.
Pascal's triangle
In mathematics, Pascal's triangle is an infinite triangular array of the binomial coefficients which play a crucial role in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Bla ...
was first illustrated in China by Yang Hui in his book ''Xiangjie Jiuzhang Suanfa'' (詳解九章算法), although it was described earlier around 1100 by Jia Xian. Although the ''Introduction to Computational Studies'' (算學啓蒙) written by Zhu Shijie (fl.
''Floruit'' ( ; usually abbreviated fl. or occasionally flor.; from Latin for 'flourished') denotes a date or period during which a person was known to have been alive or active. In English, the unabbreviated word may also be used as a noun indic ...
13th century) in 1299 contained nothing new in Chinese algebra, it had a great impact on the development of Japanese mathematics.
Algebra
''Ceyuan haijing''
'' Ceyuan haijing'' (), or ''Sea-Mirror of the Circle Measurements'', is a collection of 692 formula and 170 problems related to inscribed circle in a triangle, written by Li Zhi (or Li Ye) (1192–1272 AD). He usedTian yuan shu
''Tian yuan shu'' () is a Chinese system of algebra for polynomial equations. Some of the earliest existing writings were created in the 13th century during the Yuan dynasty. However, the tianyuanshu method was known much earlier, in the Song dy ...
to convert intricated geometry problems into pure algebra problems. He then used ''fan fa'', or Horner's method, to solve equations of degree as high as six, although he did not describe his method of solving equations. "Li Chih (or Li Yeh, 1192–1279), a mathematician of Peking who was offered a government post by Khublai Khan in 1206, but politely found an excuse to decline it. His ''Ts'e-yuan hai-ching'' (''Sea-Mirror of the Circle Measurements'') includes 170 problems dealing with ..ome of the problems leading to polynomial equations of sixth degree. Although he did not describe his method of solution of equations, it appears that it was not very different from that used by Chu Shih-chieh and Horner. Others who used the Horner method were Ch'in Chiu-shao (ca. 1202 – ca.1261) and Yang Hui (fl. ca. 1261–1275).
''Jade Mirror of the Four Unknowns''
 The '' Jade Mirror of the Four Unknowns'' was written by Zhu Shijie in 1303 AD and marks the peak in the development of Chinese algebra. The four elements, called heaven, earth, man and matter, represented the four unknown quantities in his algebraic equations. It deals with simultaneous equations and with equations of degrees as high as fourteen. The author uses the method of ''fan fa'', today called Horner's method, to solve these equations.
There are many summation series equations given without proof in the ''Mirror''. A few of the summation series are:
The '' Jade Mirror of the Four Unknowns'' was written by Zhu Shijie in 1303 AD and marks the peak in the development of Chinese algebra. The four elements, called heaven, earth, man and matter, represented the four unknown quantities in his algebraic equations. It deals with simultaneous equations and with equations of degrees as high as fourteen. The author uses the method of ''fan fa'', today called Horner's method, to solve these equations.
There are many summation series equations given without proof in the ''Mirror''. A few of the summation series are:
''Mathematical Treatise in Nine Sections''
The '' Mathematical Treatise in Nine Sections'', was written by the wealthy governor and minister Ch'in Chiu-shao () and with the invention of a method of solving simultaneous congruences, it marks the high point in Chinese indeterminate analysis.Magic squares and magic circles
The earliest knownmagic square
In mathematics, especially History of mathematics, historical and recreational mathematics, a square array of numbers, usually positive integers, is called a magic square if the sums of the numbers in each row, each column, and both main diago ...
s of order greater than three are attributed to Yang Hui (fl. ca. 1261–1275), who worked with magic squares of order as high as ten. "The same "Horner" device was used by Yang Hui, about whose life almost nothing is known and who work has survived only in part. Among his contributions that are extant are the earliest Chinese magic squares of order greater than three, including two each of orders four through eight and one each of orders nine and ten." He also worked with magic circle.
Trigonometry
The embryonic state oftrigonometry
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The fiel ...
in China slowly began to change and advance during the Song dynasty (960–1279), where Chinese mathematicians began to express greater emphasis for the need of spherical trigonometry in calendar science and astronomical calculations. The polymath
A polymath or polyhistor is an individual whose knowledge spans many different subjects, known to draw on complex bodies of knowledge to solve specific problems. Polymaths often prefer a specific context in which to explain their knowledge, ...
and official Shen Kuo
Shen Kuo (; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and Art name#China, pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁),Yao (2003), 544. was a Chinese polymath, scientist, and statesman of the Song dynasty (960� ...
(1031–1095) used trigonometric functions to solve mathematical problems of chords and arcs. Joseph W. Dauben notes that in Shen's "technique of intersecting circles" formula, he creates an approximation of the arc of a circle ''s'' by ''s'' = ''c'' + 2''v''2/''d'', where ''d'' is the diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions a ...
, ''v'' is the versine, ''c'' is the length of the chord ''c'' subtending the arc. Sal Restivo writes that Shen's work in the lengths of arcs of circles provided the basis for spherical trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the edge (geometry), sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, ge ...
developed in the 13th century by the mathematician and astronomer Guo Shoujing (1231–1316).. Gauchet and Needham state Guo used spherical trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the edge (geometry), sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, ge ...
in his calculations to improve the Chinese calendar
The traditional Chinese calendar, dating back to the Han dynasty, is a lunisolar calendar that blends solar, lunar, and other cycles for social and agricultural purposes. While modern China primarily uses the Gregorian calendar for officia ...
and astronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest includ ...
. Along with a later 17th-century Chinese illustration of Guo's mathematical proofs, Needham writes:
Despite the achievements of Shen and Guo's work in trigonometry, another substantial work in Chinese trigonometry would not be published again until 1607, with the dual publication of ''Euclid's Elements
The ''Elements'' ( ) is a mathematics, mathematical treatise written 300 BC by the Ancient Greek mathematics, Ancient Greek mathematician Euclid.
''Elements'' is the oldest extant large-scale deductive treatment of mathematics. Drawing on the w ...
'' by Chinese official and astronomer Xu Guangqi (1562–1633) and the Italian Jesuit Matteo Ricci (1552–1610).
Ming dynasty
After the overthrow of theYuan dynasty
The Yuan dynasty ( ; zh, c=元朝, p=Yuáncháo), officially the Great Yuan (; Mongolian language, Mongolian: , , literally 'Great Yuan State'), was a Mongol-led imperial dynasty of China and a successor state to the Mongol Empire after Div ...
, China became suspicious of Mongol-favored knowledge. The court turned away from math and physics in favor of botany
Botany, also called plant science, is the branch of natural science and biology studying plants, especially Plant anatomy, their anatomy, Plant taxonomy, taxonomy, and Plant ecology, ecology. A botanist or plant scientist is a scientist who s ...
and pharmacology
Pharmacology is the science of drugs and medications, including a substance's origin, composition, pharmacokinetics, pharmacodynamics, therapeutic use, and toxicology. More specifically, it is the study of the interactions that occur betwee ...
. Imperial examination
The imperial examination was a civil service examination system in History of China#Imperial China, Imperial China administered for the purpose of selecting candidates for the Civil service#China, state bureaucracy. The concept of choosing bureau ...
s included little mathematics, and what little they included ignored recent developments. Martzloff writes:
Correspondingly, scholars paid less attention to mathematics; preeminent mathematicians such as Gu Yingxiang and Tang Shunzhi appear to have been ignorant of the 'increase multiply' method. Without oral interlocutors to explicate them, the texts rapidly became incomprehensible; worse yet, most problems could be solved with more elementary methods. To the average scholar, then, ''tianyuan'' seemed numerology. When Wu Jing collated all the mathematical works of previous dynasties into ''The Annotations of Calculations in the Nine Chapters on the Mathematical Art'', he omitted ''Tian yuan shu'' and the increase multiply method.
Qing dynasty
Under theKangxi Emperor
The Kangxi Emperor (4 May 165420 December 1722), also known by his temple name Emperor Shengzu of Qing, personal name Xuanye, was the third emperor of the Qing dynasty, and the second Qing emperor to rule over China proper. His reign of 61 ...
, who learned Western mathematics from the Jesuits and was open to outside knowledge and ideas, Chinese mathematics enjoyed a brief period of official support. At Kangxi's direction, Mei Goucheng and three other outstanding mathematicians compiled a 53-volume work titled ''Shuli Jingyun'' ("The Essence of Mathematical Study") which was printed in 1723, and gave a systematic introduction to western mathematical knowledge. At the same time, Mei Goucheng also developed to ''Meishi Congshu Jiyang'' he Compiled works of Mei ''Meishi Congshu Jiyang'' was an encyclopedic summary of nearly all schools of Chinese mathematics at that time, but it also included the cross-cultural works of Mei Wending (1633–1721), Goucheng's grandfather. The enterprise sought to alleviate the difficulties for Chinese mathematicians working on Western mathematics in tracking down citations.
In 1773, the Qianlong Emperor
The Qianlong Emperor (25 September 17117 February 1799), also known by his temple name Emperor Gaozong of Qing, personal name Hongli, was the fifth Emperor of China, emperor of the Qing dynasty and the fourth Qing emperor to rule over China pr ...
decided to compile the '' Complete Library of the Four Treasuries'' (or ''Siku Quanshu''). Dai Zhen (1724–1777) selected and proofread '' The Nine Chapters on the Mathematical Art'' from ''Yongle Encyclopedia
The ''Yongle Encyclopedia'' () or ''Yongle Dadian'' () is a Chinese ''leishu'' encyclopedia commissioned by the Yongle Emperor (1402–1424) of the Ming dynasty in 1403 and completed by 1408. It comprised 22,937 manuscript rolls in 11,095 vol ...
'' and several other mathematical works from Han and Tang dynasties. The long-missing mathematical works from Song and Yuan dynasties such as ''Si-yüan yü-jian'' and '' Ceyuan haijing'' were also found and printed, which directly led to a wave of new research. The most annotated works were ''Jiuzhang suanshu xicaotushuo'' (The Illustrations of Calculation Process for ''The Nine Chapters on the Mathematical Art'' ) contributed by Li Huang and Siyuan yujian xicao (The Detailed Explanation of Si-yuan yu-jian) by Luo Shilin.
Western influences
In 1840, the First Opium War forced China to open its door and look at the outside world, which also led to an influx of western mathematical studies at a rate unrivaled in the previous centuries. In 1852, the Chinese mathematician Li Shanlan and the British missionary Alexander Wylie co-translated the later nine volumes of ''Elements'' and 13 volumes on ''Algebra''. With the assistance of Joseph Edkins, more works on astronomy and calculus soon followed. Chinese scholars were initially unsure whether to approach the new works: was study of Western knowledge a form of submission to foreign invaders? But by the end of the century, it became clear that China could only begin to recover its sovereignty by incorporating Western works. Chinese scholars, taught in Western missionary schools, from (translated) Western texts, rapidly lost touch with the indigenous tradition. Those who were self-trained or in traditionalist circles nevertheless continued to work within the traditional framework of algorithmic mathematics without resorting to Western symbolism. Yet, as Martzloff notes, "from 1911 onwards, solely Western mathematics has been practised in China."In modern China
Chinese mathematics experienced a great surge of revival following the establishment of a modern Chinese republic in 1912. Ever since then, modern Chinese mathematicians have made numerous achievements in various mathematical fields. Some famous modern ethnic Chinese mathematicians include: * Shiing-Shen Chern was widely regarded as a leader ingeometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
and one of the greatest mathematicians of the 20th century and was awarded the Wolf Prize for his contributions to mathematics.
* Ky Fan made contributions to fixed point theory, in addition to influencing nonlinear functional analysis, which have found wide application in mathematical economics and game theory, potential theory, calculus of variations, and differential equations.
* Shing-Tung Yau
Shing-Tung Yau (; ; born April 4, 1949) is a Chinese-American mathematician. He is the director of the Yau Mathematical Sciences Center at Tsinghua University and professor emeritus at Harvard University. Until 2022, Yau was the William Caspar ...
, a Fields Medal
The Fields Medal is a prize awarded to two, three, or four mathematicians under 40 years of age at the International Congress of Mathematicians, International Congress of the International Mathematical Union (IMU), a meeting that takes place e ...
laureate, has influenced both physics and mathematics, and he has been active at the interface between geometry and theoretical physics
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain, and predict List of natural phenomena, natural phenomena. This is in contrast to experimental p ...
and subsequently awarded the for his contributions.
* Terence Tao, a Fields Medal
The Fields Medal is a prize awarded to two, three, or four mathematicians under 40 years of age at the International Congress of Mathematicians, International Congress of the International Mathematical Union (IMU), a meeting that takes place e ...
laureate and child prodigy
A child prodigy is, technically, a child under the age of 10 who produces meaningful work in some domain at the level of an adult expert. The term is also applied more broadly to describe young people who are extraordinarily talented in some f ...
of Chinese heritage, was the youngest participant in the history of the International Mathematical Olympiad
The International Mathematical Olympiad (IMO) is a mathematical olympiad for pre-university students, and is the oldest of the International Science Olympiads. It is widely regarded as the most prestigious mathematical competition in the wor ...
at the age of 10, winning a bronze, silver, and gold medal. He remains the youngest winner of each of the three medals in the Olympiad's history.
* Yitang Zhang, a number theorist who established the first finite bound on gaps between prime numbers.
* Chen Jingrun, a number theorist who proved that every sufficiently large even number can be written as the sum of either two primes, or a prime and a semiprime, which is now called Chen's theorem
In number theory, Chen's theorem states that every sufficiently large parity (mathematics), even number can be written as the sum of either two prime number, primes, or a prime and a semiprime (the product of two primes).
It is a weakened form o ...
. His work was important for research of Goldbach's conjecture
Goldbach's conjecture is one of the oldest and best-known list of unsolved problems in mathematics, unsolved problems in number theory and all of mathematics. It states that every even and odd numbers, even natural number greater than 2 is the ...
.
People's Republic of China
In 1949, at the beginning of the founding of the People's Republic of China, the government paid great attention to the cause of science although the country was in a predicament of lack of funds. The Chinese Academy of Sciences was established in November 1949. The Institute of Mathematics was formally established in July 1952. Then, the Chinese Mathematical Society and its founding journals restored and added other special journals. In the 18 years after 1949, the number of published papers accounted for more than three times the total number of articles before 1949. Many of them not only filled the gaps in China's past, but also reached the world's advanced level. During the chaos of theCultural Revolution
The Cultural Revolution, formally known as the Great Proletarian Cultural Revolution, was a Social movement, sociopolitical movement in the China, People's Republic of China (PRC). It was launched by Mao Zedong in 1966 and lasted until his de ...
, the sciences declined. In the field of mathematics, in addition to Chen Jingrun, Hua Luogeng, Zhang Guanghou and other mathematicians struggling to continue their work. After the catastrophe, with the publication of Guo Moruo's literary "Spring of Science", Chinese sciences and mathematics experienced a revival. In 1977, a new mathematical development plan was formulated in Beijing, the work of the mathematics society was resumed, the journal was re-published, the academic journal was published, the mathematics education was strengthened, and basic theoretical research was strengthened.
An important mathematical achievement of the Chinese mathematician in the direction of the power system is how Xia Zhihong proved the Painleve conjecture in 1988. When there are some initial states of ''N'' celestial bodies, one of the celestial bodies ran to infinity or speed in a limited time. Infinity is reached, that is, there are non-collision singularities. The Painleve conjecture is an important conjecture in the field of power systems proposed in 1895. A very important recent development for the 4-body problem is that Xue Jinxin and Dolgopyat proved a non-collision singularity in a simplified version of the 4-body system around 2013.
In addition, in 2007, Shen Weixiao and Kozlovski, Van-Strien proved the Real Fatou conjecture: Real hyperbolic polynomials are dense in the space of real polynomials with fixed degree. This conjecture can be traced back to Fatou in the 1920s, and later Smale posed it in the 1960s. The proof of Real Fatou conjecture is one of the most important developments in conformal dynamics in the past decade.
IMO performance
In comparison to other participating countries at theInternational Mathematical Olympiad
The International Mathematical Olympiad (IMO) is a mathematical olympiad for pre-university students, and is the oldest of the International Science Olympiads. It is widely regarded as the most prestigious mathematical competition in the wor ...
, China has highest team scores and has won the all-members-gold IMO with a full team the most number of times.
In education
The first reference to a book being used in learning mathematics in China is dated to the second century CE ( Hou Hanshu: 24, 862; 35,1207). Ma Xu, who is a youth , and Zheng Xuan (127–200) both studied the ''Nine Chapters on Mathematical procedures''. Christopher Cullen claims that mathematics, in a manner akin to medicine, was taught orally. The stylistics of the '' Suàn shù shū'' from Zhangjiashan suggest that the text was assembled from various sources and then underwent codification.See also
*Chinese astronomy
Astronomy in China has a long history stretching from the Shang dynasty, being refined over a period of more than 3,000 years. The Ancient China, ancient Chinese people have identified stars from 1300 BCE, as Chinese star names later categori ...
* History of mathematics
The history of mathematics deals with the origin of discoveries in mathematics and the History of mathematical notation, mathematical methods and notation of the past. Before the modern age and the worldwide spread of knowledge, written examples ...
** Indian mathematics
** Islamic mathematics
** Japanese mathematics
* List of Chinese discoveries
* List of Chinese mathematicians
*Chinese numerology, Numbers in Chinese culture
References
Citations
Works cited
* * * * * * * * * * * * * * * * *External links
Early mathematics texts
(Chinese) - Chinese Text Project
Overview of Chinese mathematics
Primer of Mathematics
by Zhu Shijie {{DEFAULTSORT:Chinese mathematics Chinese mathematics,