HOME

TheInfoList



Click Here for Items Related To - Cantor function
OR:
Cantor function on:   [Wikipedia]   [Google]   [Amazon]

In
mathematics Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, the Cantor function is an example of a
function Function or functionality may refer to: Computing * Function key, a type of key on computer keyboards * Function model, a structured representation of processes in a system * Function object or functor or functionoid, a concept of object-orie ...
that is
continuous Continuity or continuous may refer to: Mathematics * Continuity (mathematics), the opposing concept to discreteness; common examples include ** Continuous probability distribution or random variable in probability and statistics ** Continuous ...
, but not
absolutely continuous In calculus and real analysis, absolute continuity is a smoothness property of functions that is stronger than continuity and uniform continuity. The notion of absolute continuity allows one to obtain generalizations of the relationship betwe ...
. It is a notorious
counterexample A counterexample is any exception to a generalization. In logic a counterexample disproves the generalization, and does so rigorously in the fields of mathematics and philosophy. For example, the fact that "student John Smith is not lazy" is a c ...
in analysis, because it challenges naive intuitions about continuity,
derivative In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...
, and measure. Although it is continuous everywhere, and has zero derivative almost everywhere, its value still goes from 0 to 1 as its argument goes from 0 to 1. Thus, while the function seems like a constant one that cannot grow, it does indeed monotonically grow. It is also called the Cantor ternary function, the Lebesgue function, Lebesgue's singular function, the Cantor–Vitali function, the Devil's staircase, the Cantor staircase function, and the Cantor–Lebesgue function. introduced the Cantor function and mentioned that Scheeffer pointed out that it was a
counterexample A counterexample is any exception to a generalization. In logic a counterexample disproves the generalization, and does so rigorously in the fields of mathematics and philosophy. For example, the fact that "student John Smith is not lazy" is a c ...
to an extension of the
fundamental theorem of calculus The fundamental theorem of calculus is a theorem that links the concept of derivative, differentiating a function (mathematics), function (calculating its slopes, or rate of change at every point on its domain) with the concept of integral, inte ...
claimed by Harnack. The Cantor function was discussed and popularized by , , and .


Definition

To define the Cantor function c: ,1to ,1/math>, let x be any number in ,1/math> and obtain c(x) by the following steps: #Express x in base 3, using digits 0, 1, 2. #If the base-3 representation of x contains a 1, replace every digit strictly after the first 1 with 0. #Replace any remaining 2s with 1s. #Interpret the result as a binary number. The result is c(x). For example: *\tfrac14 has the ternary representation 0.02020202... There are no 1s so the next stage is still 0.02020202... This is rewritten as 0.01010101... This is the binary representation of \tfrac13, so c(\tfrac14)=\tfrac13. *\tfrac15 has the ternary representation 0.01210121... The digits after the first 1 are replaced by 0s to produce 0.01000000... This is not rewritten since it has no 2s. This is the binary representation of \tfrac14, so c(\tfrac15)=\tfrac14. *\tfrac has the ternary representation 0.21102 (or 0.211012222...). The digits after the first 1 are replaced by 0s to produce 0.21. This is rewritten as 0.11. This is the binary representation of \tfrac34, so c(\tfrac)=\tfrac34. Equivalently, if \mathcal is the
Cantor set In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and mentioned by German mathematician Georg Cantor in 1883. Throu ...
on ,1 then the Cantor function c: ,1to ,1/math> can be defined as c(x) =\begin \displaystyle \sum_^\infty \frac, & \displaystyle \text x = \sum_^\infty \frac\in\mathcal\ \text\ a_n\in\; \\ \displaystyle \sup_ c(y), & \displaystyle \text x\in ,1\setminus \mathcal. \end This formula is well-defined, since every member of the Cantor set has a ''unique'' base 3 representation that only contains the digits 0 or 2. (For some members of \mathcal, the ternary expansion is repeating with trailing 2's and there is an alternative non-repeating expansion ending in 1. For example, \tfrac13 = 0.13 = 0.02222...3 is a member of the Cantor set). Since c(0)=0 and c(1)=1, and c is monotonic on \mathcal, it is clear that 0\le c(x)\le 1 also holds for all x\in ,1smallsetminus\mathcal.


Properties

The Cantor function challenges naive intuitions about continuity and measure; though it is continuous everywhere and has zero derivative
almost everywhere In measure theory (a branch of mathematical analysis), a property holds almost everywhere if, in a technical sense, the set for which the property holds takes up nearly all possibilities. The notion of "almost everywhere" is a companion notion to ...
, c(x) goes from 0 to 1 as uniformly continuous In mathematics, a real function f of real numbers is said to be uniformly continuous if there is a positive real number \delta such that function values over any function domain interval of the size \delta are as close to each other as we want. In ...
(precisely, it is
Hölder continuous Hölder: * ''Hölder, Hoelder'' as surname * Hölder condition * Hölder's inequality In mathematical analysis, Hölder's inequality, named after Otto Hölder, is a fundamental inequality (mathematics), inequality between Lebesgue integration, in ...
of exponent \alpha = \log_3(2)) but not
absolutely continuous In calculus and real analysis, absolute continuity is a smoothness property of functions that is stronger than continuity and uniform continuity. The notion of absolute continuity allows one to obtain generalizations of the relationship betwe ...
. It is constant on intervals of the form (0.''x''1''x''2''x''3...''x''n022222..., 0.''x''1''x''2''x''3...''x''n200000...), and every point not in the Cantor set is in one of these intervals, so its derivative is 0 outside of the Cantor set. On the other hand, it has no
derivative In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...
at any point in an
uncountable In mathematics, an uncountable set, informally, is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger tha ...
subset of the
Cantor set In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and mentioned by German mathematician Georg Cantor in 1883. Throu ...
containing the interval endpoints described above. The Cantor function can also be seen as the
cumulative probability distribution function In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x. Ever ...
of the 1/2-1/2 Bernoulli measure ''μ'' supported on the Cantor set: c(x)=\mu( ,x. This probability distribution, called the
Cantor distribution The Cantor distribution is the probability distribution whose cumulative distribution function is the Cantor function. This distribution has neither a probability density function nor a probability mass function, since although its cumulative ...
, has no discrete part. That is, the corresponding measure is atomless. This is why there are no jump discontinuities in the function; any such jump would correspond to an atom in the measure. However, no non-constant part of the Cantor function can be represented as an integral of a
probability density function In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a Function (mathematics), function whose value at any given sample (or point) in the sample space (the s ...
; integrating any putative
probability density function In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a Function (mathematics), function whose value at any given sample (or point) in the sample space (the s ...
that is not
almost everywhere In measure theory (a branch of mathematical analysis), a property holds almost everywhere if, in a technical sense, the set for which the property holds takes up nearly all possibilities. The notion of "almost everywhere" is a companion notion to ...
zero over any interval will give positive probability to some interval to which this distribution assigns probability zero. In particular, as pointed out, the function is not the integral of its derivative even though the derivative exists almost everywhere. The Cantor function is the standard example of a singular function. The Cantor function is also a standard example of a function with
bounded variation In mathematical analysis, a function of bounded variation, also known as ' function, is a real number, real-valued function (mathematics), function whose total variation is bounded (finite): the graph of a function having this property is well beh ...
but, as mentioned above, is not absolutely continuous. However, every absolutely continuous function is continuous with bounded variation. The Cantor function is non-decreasing, and so in particular its graph defines a
rectifiable curve Arc length is the distance between two points along a section of a curve. Development of a formulation of arc length suitable for applications to mathematics and the sciences is a problem in vector calculus and in differential geometry. In the ...
. showed that the arc length of its graph is 2. Note that the graph of any nondecreasing function such that f(0)=0 and f(1)=1 has length not greater than 2. In this sense, the Cantor function is extremal.


Lack of absolute continuity

The
Lebesgue measure In measure theory, a branch of mathematics, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of higher dimensional Euclidean '-spaces. For lower dimensions or , it c ...
of the
Cantor set In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and mentioned by German mathematician Georg Cantor in 1883. Throu ...
is 0. Therefore, for any positive ''ε'' < 1 and any ''δ'' > 0, there exists a finite sequence of
pairwise disjoint In set theory in mathematics and Logic#Formal logic, formal logic, two Set (mathematics), sets are said to be disjoint sets if they have no element (mathematics), element in common. Equivalently, two disjoint sets are sets whose intersection (se ...
sub-intervals with total length < ''δ'' over which the Cantor function cumulatively rises more than ''ε''. In fact, for every ''δ'' > 0 there are finitely many pairwise disjoint intervals (''xk'',''yk'') (1 ≤ ''k'' ≤ ''M'') with \sum\limits_^M (y_k-x_k)<\delta and \sum\limits_^M (c(y_k)-c(x_k))=1.


Alternative definitions


Iterative construction

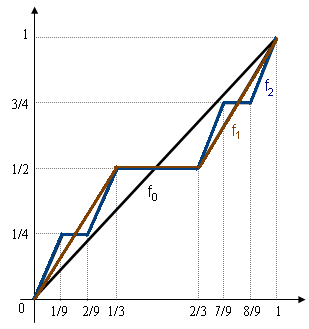Below we define a sequence (f_n)_n of functions on the unit interval that converges to the Cantor function. Let f_0(x) = x. Then, for every integer n \geq 0, the next function f_(x) will be defined in terms of f_n(x) as follows:f_(x) = \begin \displaystyle \frac f_n(3 x) &\text 0 \leq x \leq \frac \\ \displaystyle \frac &\text \frac \leq x \leq \frac \\ \displaystyle \frac + \frac f_n(3 x - 2) &\text \frac \leq x \leq 1 \endThe three definitions are compatible at the end-points \tfrac and \tfrac, because f_n(0) = 0 and f_n(1) = 1 for every n, by induction. One may check that (f_n)_n converges pointwise to the Cantor function defined above. Furthermore, the convergence is uniform. Indeed, separating into three cases, according to the definition of f_, one sees that :\max_ , f_(x) - f_n(x), \le \frac 1 2 \, \max_ , f_(x) - f_(x), , \quad n \ge 1. If f denotes the limit function, it follows that, for every n \geq 0, :\max_ , f(x) - f_n(x), \le 2^ \, \max_ , f_1(x) - f_0(x), .


Fractal volume

The Cantor function is closely related to the
Cantor set In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and mentioned by German mathematician Georg Cantor in 1883. Throu ...
. The Cantor set ''C'' can be defined as the set of those numbers in the interval , 1that do not contain the digit 1 in their base-3 (triadic) expansion, except if the 1 is followed by zeros only (in which case the tail 1000\ldots can be replaced by 0222\ldots to get rid of any 1). It turns out that the Cantor set is a
fractal In mathematics, a fractal is a Shape, geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scale ...
with (uncountably) infinitely many points (zero-dimensional volume), but zero length (one-dimensional volume). Only the ''D''-dimensional volume H_D (in the sense of a Hausdorff-measure) takes a finite value, where D = \log_3(2) is the fractal dimension of ''C''. We may define the Cantor function alternatively as the ''D''-dimensional volume of sections of the Cantor set : f(x)=H_D(C \cap (0,x)).


Self-similarity

The Cantor function possesses several
symmetries Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is invariant under some transformations ...
. For 0\le x\le 1, there is a reflection symmetry :c(x)=1-c(1-x) and a pair of magnifications, one on the left and one on the right: :c\left(\frac\right) = \frac and :c\left(\frac\right) = \frac The magnifications can be cascaded; they generate the
dyadic monoid In mathematics, the modular group is the projective special linear group \operatorname(2,\mathbb Z) of 2\times 2 matrices with integer coefficients and determinant 1, such that the matrices A and -A are identified. The modular group acts on th ...
. This is exhibited by defining several helper functions. Define the reflection as :r(x)=1-x The first self-symmetry can be expressed as :r\circ c = c\circ r where the symbol \circ denotes function composition. That is, (r\circ c)(x)=r(c(x))=1-c(x) and likewise for the other cases. For the left and right magnifications, write the left-mappings :L_D(x)= \frac and L_C(x)= \frac Then the Cantor function obeys :L_D \circ c = c \circ L_C Similarly, define the right mappings as :R_D(x)= \frac and R_C(x)= \frac Then, likewise, :R_D \circ c = c \circ R_C The two sides can be mirrored one onto the other, in that :L_D \circ r = r\circ R_D and likewise, :L_C \circ r = r\circ R_C These operations can be stacked arbitrarily. Consider, for example, the sequence of left-right moves LRLLR. Adding the subscripts C and D, and, for clarity, dropping the composition operator \circ in all but a few places, one has: :L_D R_D L_D L_D R_D \circ c = c \circ L_C R_C L_C L_C R_C Arbitrary finite-length strings in the letters L and R correspond to the dyadic rationals, in that every dyadic rational can be written as both y=n/2^m for integer ''n'' and ''m'' and as finite length of bits y=0.b_1b_2b_3\cdots b_m with b_k\in \. Thus, every dyadic rational is in one-to-one correspondence with some self-symmetry of the Cantor function. Some notational rearrangements can make the above slightly easier to express. Let g_0 and g_1 stand for L and R. Function composition extends this to a
monoid In abstract algebra, a monoid is a set equipped with an associative binary operation and an identity element. For example, the nonnegative integers with addition form a monoid, the identity element being . Monoids are semigroups with identity ...
, in that one can write g_=g_0g_1g_0 and generally, g_Ag_B=g_ for some binary strings of digits ''A'', ''B'', where ''AB'' is just the ordinary
concatenation In formal language theory and computer programming, string concatenation is the operation of joining character strings end-to-end. For example, the concatenation of "snow" and "ball" is "snowball". In certain formalizations of concatenati ...
of such strings. The dyadic monoid ''M'' is then the monoid of all such finite-length left-right moves. Writing \gamma\in M as a general element of the monoid, there is a corresponding self-symmetry of the Cantor function: :\gamma_D\circ c= c\circ \gamma_C The dyadic monoid itself has several interesting properties. It can be viewed as a finite number of left-right moves down an infinite
binary tree In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the ''left child'' and the ''right child''. That is, it is a ''k''-ary tree with . A recursive definition using set theor ...
; the infinitely distant "leaves" on the tree correspond to the points on the Cantor set, and so, the monoid also represents the self-symmetries of the Cantor set. In fact, a large class of commonly occurring fractals are described by the dyadic monoid; additional examples can be found in the article on
de Rham curve In mathematics, a de Rham curve is a continuous fractal curve obtained as the image of the Cantor space, or, equivalently, from the base-two expansion of the real numbers in the unit interval. Many well-known fractal curves, including the Cantor ...
s. Other fractals possessing self-similarity are described with other kinds of monoids. The dyadic monoid is itself a sub-monoid of the
modular group In mathematics, the modular group is the projective special linear group \operatorname(2,\mathbb Z) of 2\times 2 matrices with integer coefficients and determinant 1, such that the matrices A and -A are identified. The modular group acts on ...
SL(2,\mathbb). Note that the Cantor function bears more than a passing resemblance to
Minkowski's question-mark function In mathematics, Minkowski's question-mark function, denoted , is a function with unusual fractal properties, defined by Hermann Minkowski in 1904. It maps quadratic irrational numbers to rational numbers on the unit interval, via an expressio ...
. In particular, it obeys the exact same symmetry relations, although in an altered form.


Generalizations

Let : y=\sum_^\infty b_k 2^ be the dyadic (binary) expansion of the real number 0 ≤ ''y'' ≤ 1 in terms of binary digits ''b''''k'' ∈ . This expansion is discussed in greater detail in the article on the
dyadic transformation The dyadic transformation (also known as the dyadic map, bit shift map, 2''x'' mod 1 map, Bernoulli map, doubling map or sawtooth map) is the mapping (i.e., recurrence relation) : T: , 1) \to [0, 1)^\infty : x \mapsto (x_0, x_1, x_2, ...
. Then consider the function : C_z(y)=\sum_^\infty b_k z^. For ''z'' = 1/3, the inverse of the function ''x'' = 2 ''C''1/3(''y'') is the Cantor function. That is, ''y'' = ''y''(''x'') is the Cantor function. In general, for any ''z'' < 1/2, ''C''''z''(''y'') looks like the Cantor function turned on its side, with the width of the steps getting wider as ''z'' approaches zero. As mentioned above, the Cantor function is also the cumulative distribution function of a measure on the Cantor set. Different Cantor functions, or Devil's Staircases, can be obtained by considering different atom-less probability measures supported on the Cantor set or other fractals. While the Cantor function has derivative 0 almost everywhere, current research focuses on the question of the size of the set of points where the upper right derivative is distinct from the lower right derivative, causing the derivative to not exist. This analysis of differentiability is usually given in terms of fractal dimension, with the Hausdorff dimension the most popular choice. This line of research was started in the 1990s by Darst, who showed that the Hausdorff dimension of the set of non-differentiability of the Cantor function is the square of the dimension of the Cantor set, (\log_3(2))^2. Subsequently Falconer showed that this squaring relationship holds for all Ahlfors's regular, singular measures, i.e.\dim_H\left\=\left(\dim_H\operatorname(\mu)\right)^2Later, Troscheit obtain a more comprehensive picture of the set where the derivative does not exist for more general normalized Gibb's measures supported on self-conformal and self-similar sets.
Hermann Minkowski Hermann Minkowski (22 June 1864 – 12 January 1909) was a mathematician and professor at the University of Königsberg, the University of Zürich, and the University of Göttingen, described variously as German, Polish, Lithuanian-German, o ...
's question mark function loosely resembles the Cantor function visually, appearing as a "smoothed out" form of the latter; it can be constructed by passing from a continued fraction expansion to a binary expansion, just as the Cantor function can be constructed by passing from a ternary expansion to a binary expansion. The question mark function has the interesting property of having vanishing derivatives at all rational numbers.


See also

*
Dyadic transformation The dyadic transformation (also known as the dyadic map, bit shift map, 2''x'' mod 1 map, Bernoulli map, doubling map or sawtooth map) is the mapping (i.e., recurrence relation) : T: , 1) \to , 1)^\infty : x \mapsto (x_0, x_1, x_2, ...
* Weierstrass function, a function that is continuous everywhere but differentiable nowhere.


Notes


References

* * Reprinted in: E. Zermelo (Ed.), Gesammelte Abhandlungen Mathematischen und Philosophischen Inhalts, Springer, New York, 1980. * * * * * * * * *


External links


''Cantor ternary function'' at Encyclopaedia of Mathematics

Cantor Function
by Douglas Rivers, the Wolfram Demonstrations Project. * {{fractals, state=collapsed Fractals Measure theory Special functions Georg Cantor De Rham curves