CIE XYZ Color Space

In 1931, the International Commission on Illumination (CIE) published the CIE 1931 color spaces which define the relationship between the visible spectrum and human color vision. The CIE color spaces are mathematical models that comprise a "standard observer", which is a static idealization of the color vision of a normal human. A useful application of the CIEXYZ colorspace is that a mixture of two colors in some proportion lies on the straight line between those two colors. One disadvantage is that it is not perceptually uniform. This disadvantage is remedied in subsequent color models such as CIELUV and CIELAB, but these and modern color models still use the CIE 1931 color spaces as a foundation.

The CIE (from the French name " Commission Internationale de l'éclairage" - International Commission on Illumination) developed and maintains many of the standards in use today relating to colorimetry. The CIE color spaces were created using data from a series of experiments, where human test subjects adjusted red, green, and blue primary colors to find a visual match to a second, pure color. The original experiments were conducted in the mid-1920s by William David Wright using ten observers and John Guild using seven observers. The experimental results were combined, creating the CIE RGB color space. The CIE XYZ color space was derived from CIE RGB in an effort to simplify the math.

These color spaces are fundamental tools for measuring color for industry, including inks, dyes, and paints, illumination, color imaging, etc. The CIE color spaces contributed to the development of color television, the creation of instruments for maintaining consistent color in manufacturing processes, and other methods of color management.

Background

Color vision

Normal human color vision is trichromatic, which is enabled by three classes of cone cells (L, M & S). Each cone class contains a slightly different photopsin with a different spectral sensitivity. The spectral sensitivities are summarized by their peak wavelengths, which are at long ("L", ), medium ("M", ), and short ("S", ) wavelengths, sometimes shorthanded inexactly as red, green and blue cones, respectively. The differential excitation levels of these three cones comprise the tristimulus values, denoted "L", "M", and "S", and are the parameters that define the 3-dimensional "LMS color space", which is one of many color spaces devised to quantify human color vision. In principle, any human color sensation can be described by a set of tristimulus values. A continuous spectral power distribution of light $S(\lambda)$ is converted to the discrete tristimulus values (in this case $L$, $M$ & $S$) by integrating over a spectral sensitivity of one of the cone classes ($\overline(\lambda)$, $\overline(\lambda)$, or $\overline(\lambda)$):
:\begin
L &= \int_0^\infty S(\lambda)\,\overline(\lambda)\,d\lambda, \\ muM &= \int_0^\infty S(\lambda)\,\overline(\lambda)\,d\lambda, \\ muS &= \int_0^\infty S(\lambda)\,\overline(\lambda)\,d\lambda.
\end

These are all inner products and can be thought of as a projection of an infinite-dimensional spectrum to a three-dimensional color. This LMS color model is refined to the LMS color space when the spectral sensitivity " primaries" are defined according to the standard observer. The LMS color space can be further transformed into similar three-dimensional color spaces, such as RGB, XYZ, HSV or cognates thereof. The tristimulus values associated with a color space can be conceptualized as amounts of three primary colors in a trichromatic, additive color model. In some color spaces, including the LMS and XYZ spaces, the primary colors used are not real colors in the sense that they cannot be generated in any spectral power distribution of light.

Metamerism and Grassmann's laws

Since a lot of information is lost during the conversion (projection) of a continuous light spectrum to tristimulus values, it follows that there are disparate spectra that can stimulate the same tristimulus values. These disparate spectra are known as metamers. For example, a monochromatic (yellow) light is ''metameric'' with a dichromatic light spectrum comprising 2 parts monochromatic (green) light and 1 part monochromatic (red) light (accounting for luminosity). In 1853, Hermann Grassmann developed Grassmann's laws, which aimed to describe color mixing algebraically. These laws laid the theoretical framework necessary for color experiments performed by Hermann von Helmholtz (remembered for popularizing the trichromatic theory) and James Clerk Maxwell in the 1850's, and later in the experiments used to develop the CIE 1931 color spaces. The laws can be summarized in three principles:
* Additivity: if a third light (z) is added equally to two metamers (a & b), the results are metamers (i.e. if a = b then a + z = b + z).
* Proportionality: if the luminances of two metamers are equally increased or reduced by some constant (m), the results are metamers (i.e. if a = b then a*m = b*m).
* Transitivity: If one of two metamers is metameric with a third color, then all colors are metameric (i.e. If a = b and b = c, then a = c)
These laws assume that human color vision is linear, which is approximately true, but non-linear effects (such as the Helmholtz–Kohlrausch effect) are not considered in the CIE 1931 color model.

Origin

The CIE 1931 color spaces are 4 interrelated color spaces with the same origin. In the 1920s, two independent experiments on human color perception were conducted by W. David Wright with ten observers, and John Guild with seven observers. How their results laid the foundation of the CIE 1931 color spaces is described in this section.

CIE standard observer

These experiments sought to quantify the typical human chromatic response (color perception) and define it as the standard (colorimetric) observer. The standard observer is defined by the 3 color matching functions in one of the CIE 1931 color spaces. Due to the design of the experiments, the standard observer has the following constraints:
* Due to the distribution of cones in the eye, the tristimulus values depend on the observer's field of view. The standard observer was limited to stimuli subtending the 2° arc inside the fovea of the retina. This angle was chosen owing to the belief that the color-sensitive cones resided within a 2° arc of the fovea. This original observer is often referred to as the ''2° Standard Observer'', in contrast to a later (and less commonly used) alternative using 10° stimuli and referred to as the ''10° standard observer'', which is discussed later.
* It is applicable for brightnesses that range from mid-mesopic to photopic light.
* It is applicable only to additive color mixing, not subtractive color mixing.

Color matching

The Wright–Guild color matching experiments were conducted using a circular color screen split into equal semicircles (a bipartite field). The screen was positioned at a distance from the subject (observer) such that its diameter subtended 2° of the subject's vision. In one half of the screen, a test (target) color was projected, while on the other half an observer-adjustable color was projected. The adjustable color was a mixture of three monochromatic primary colors, each with adjustable brightness. The subject would alter the brightness of each of the three primary beams until the halves appeared metameric.

If the test color were simply a monochromatic color at wavelength λ, and if it could be matched by a combination of the three primaries at relative intensities $\bar(\lambda)$, $\bar(\lambda)$, and $\bar(\lambda)$ respectively, then a tabulation of these values at various λ will estimate three functions of wavelength. These are the RGB color-matching functions. Any spectral distribution can be thought of as a combination of a number of monochromatic sources at varying intensities, so that (by Grassmann's laws) integrating the color-matching functions with that spectral distribution will yield the intensities of the three primaries necessary to match it. The problem is that the three primaries can only produce colors which lie within their gamut the triangle in color space formed by the primaries, which never touches the monochromatic locus nor the purple line except at the three primaries. In other words, there is no monochromatic target that can be matched by a combination of the three primaries, except at the wavelengths of the three primaries themselves. Matching a monochromatic target would require one of the primaries to have a negative brightness. While this is physically impossible, it can be approximated (relying on Grassmann's laws) by adding the negative primary to the target field instead of the adjustment field, thereby allowing a match to be made with negative primary brightness.

For wavelengths between the blue and green primaries, some red primary must be added to the target, resulting in negative values of $\bar(\lambda)$. Likewise, between the green and red primaries, some blue must be added to the target, resulting in negative values of $\bar(\lambda)$. For wavelengths below the wavelength of the blue primary, or above the wavelength of the red primary, some green must be added and $\bar(\lambda)$ will be negative. For every spectral color, except those defined by the primary colors, there will always be two positive color-matching functions and one negative (as long as the primaries are all monochromatic). It can be seen (in the chromaticity diagram to the right) that the deviation of the boundaries of the triangular CIE RGB gamut align well with the spectral locus of the ''xy'' chromaticity diagram, except between the blue and green primaries, where rather large amounts of the red primary must be added to the test field, and it is in this band that the red color-matching function has the most significant negative values.

CIE RGB color space

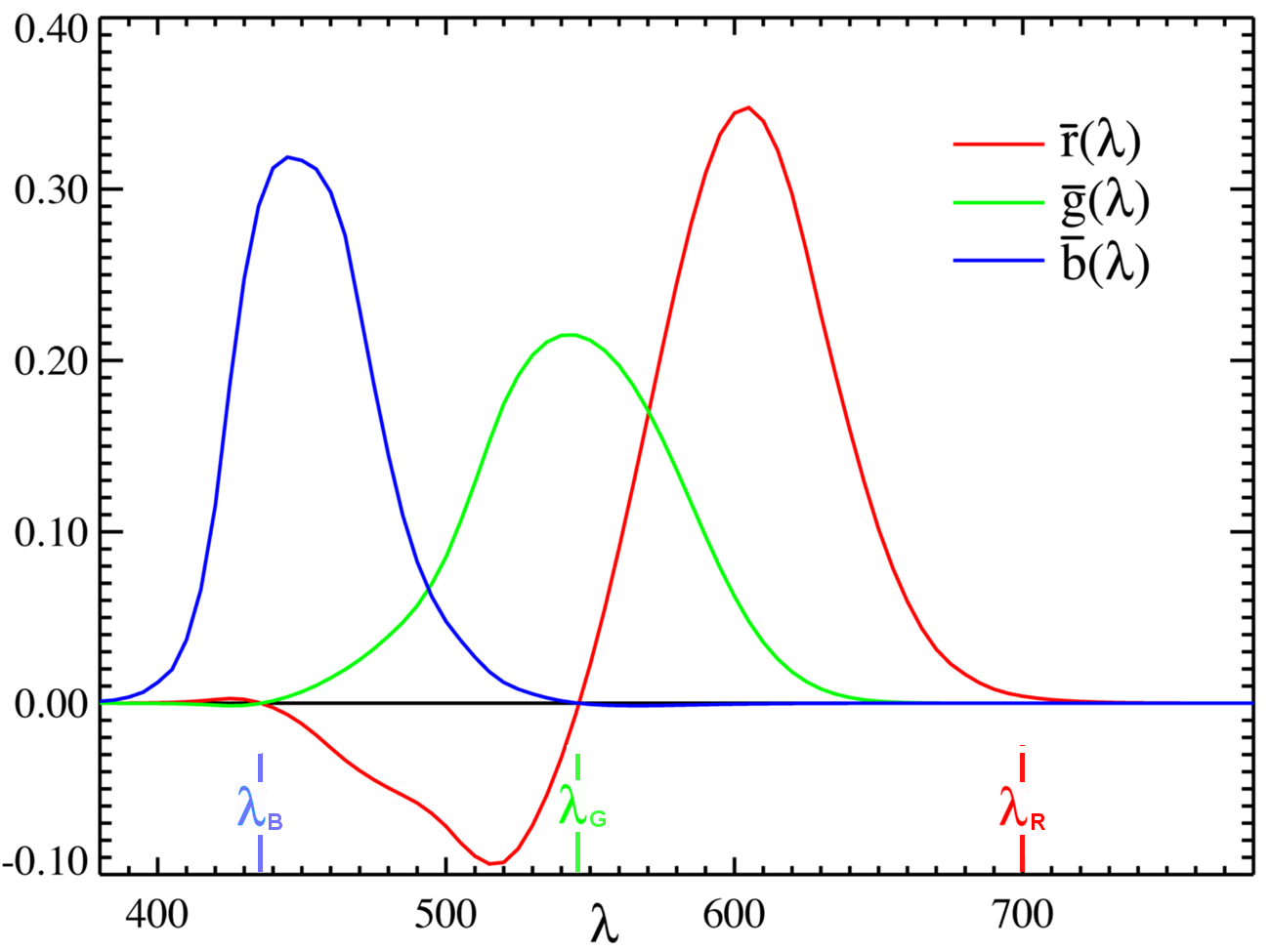
The CIE RGB color space is one of many RGB color spaces, each distinguished by their particular set of primary colors. Although Wright and Guild's experiments were carried out using various primaries at various intensities, and although they used a number of different observers, all of their results were summarized by the standardized CIE RGB color matching functions $\overline(\lambda)$, $\overline(\lambda)$, and $\overline(\lambda)$, obtained using three monochromatic primaries at standardized wavelengths of (red), (green) and (blue). The primaries with wavelengths and were chosen because they are easily reproducible monochromatic lines of a mercury vapor discharge. The wavelength, which in 1931 was difficult to reproduce as a monochromatic beam, was chosen because the eye's perception of color is rather unchanging at this wavelength, and therefore small errors in wavelength of this primary would have little effect on the results. The (un-normalized) color matching functions are the amounts of primaries needed to match the monochromatic target color. These functions are shown in the plot on the right. Note how $\overline(\lambda)$ and $\overline(\lambda)$ are zero at , $\overline(\lambda)$ and $\overline(\lambda)$ are zero at and $\overline(\lambda)$ and $\overline(\lambda)$ are zero at , since in these cases the test color is exactly equal to the non-zero primary.

The color matching functions and primaries were settled upon by a CIE special commission after considerable deliberation. and The cut-offs at the short- and long-wavelength side of the diagram are chosen somewhat arbitrarily; the human eye can actually see light with wavelengths up to about , but with a sensitivity that is many thousand times lower than for green light. These color matching functions define what is known as the "1931 CIE standard observer". Rather than specify the brightness of each primary, the curves are normalized to have constant area beneath them. This area is fixed to a particular value by specifying that:
:$\int_0^\infty \overline(\lambda)\,d\lambda = \int_0^\infty \overline(\lambda)\,d\lambda = \int_0^\infty \overline(\lambda)\,d\lambda.$

The resulting normalized color matching functions are then scaled in the r:g:b ratio of 1:4.5907:0.0601 for source luminance and 72.0962:1.3791:1 for source radiance to reproduce the true color matching functions. By proposing that the primaries be standardized, the CIE established an international system of objective color notation.

Given these scaled color matching functions, the RGB tristimulus values for
a color with a spectral power distribution $S(\lambda)$ would then be given by:
:\begin
R &= \int_0^\infty S(\lambda)\,\overline(\lambda)\,d\lambda, \\ muG &= \int_0^\infty S(\lambda)\,\overline(\lambda)\,d\lambda, \\ muB &= \int_0^\infty S(\lambda)\,\overline(\lambda)\,d\lambda.
\end

These are all inner products and can be thought of as a projection of an infinite-dimensional spectrum to a three-dimensional color.

CIE XYZ color space

After the definition of the RGB model of human vision using the CIE RGB matching functions, the CIE special commission wished to derive another color space from the CIE RGB color space. It was assumed that Grassmann's law held, and the new space would be related to the CIE RGB space by a linear transformation. The new space would be defined in terms of three new color matching functions
$\overline(\lambda)$, $\overline(\lambda)$, and $\overline(\lambda)$, which would be chosen as having the following desirable properties:

# The new color matching functions were to be everywhere greater than or equal to zero. In 1931, computations were done by hand or slide rule, and the specification of positive values was a useful computational simplification.
# The $\overline(\lambda)$ color matching function would be exactly equal to the photopic luminous efficiency function ''V''(''λ'') for the "CIE standard photopic observer". The luminance function describes the variation of perceived brightness with wavelength. The fact that the luminance function could be constructed by a linear combination of the RGB color matching functions was not guaranteed by any means but might be expected to be nearly true due to the near-linear nature of human sight. Again, the main reason for this requirement was computational simplification.
# For the constant energy white point, it was required that .
# By virtue of the definition of chromaticity and the requirement of positive values of ''x'' and ''y'', it can be seen that the gamut of all colors will lie inside the triangle , 0 , 0 , 1 It was required that the gamut fill this space practically completely.
# It was found that the $\overline(\lambda)$ color matching function could be set to zero above while remaining within the bounds of experimental error. For computational simplicity, it was specified that this would be so.

The derived CIE XYZ color space encompasses all color sensations that are perceptible to a typical human. The underlying color matching functions can be thought of as the spectral sensitivity curves of three linear light detectors yielding the CIE tristimulus values ''X'', ''Y'' and ''Z''. Collectively, these three functions describe the CIE standard observer. That is why CIE XYZ tristimulus values are a device-invariant representation of color. It serves as a standard reference against which many other color spaces are defined. A set of color-matching functions, like the spectral sensitivity curves of the LMS color space, but not restricted to non-negative sensitivities, associates physically produced light spectra with specific tristimulus values.

Most wavelengths stimulate two or all three kinds of cone cell because the spectral sensitivity curves of the three kinds overlap. Certain tristimulus values are thus physically impossible: e.g. LMS tristimulus values that are non-zero for the M component and zero for both the L and S components. Furthermore pure spectral colors would, in any normal trichromatic additive color space, e.g., the RGB color spaces, imply negative values for at least one of the three primaries because the chromaticity would be outside the color triangle defined by the primary colors. To avoid these negative RGB values, and to have one component that describes the perceived brightness, "imaginary" primary colors and corresponding color-matching functions were formulated. The CIE 1931 color space defines the resulting tristimulus values, in which they are denoted by "X", "Y", and "Z". In XYZ space, all combinations of non-negative coordinates are meaningful, but many, such as the primary locations , 0, 0 , 1, 0 and , 0, 1 correspond to imaginary colors outside the space of possible LMS coordinates; imaginary colors do not correspond to any spectral distribution of wavelengths and therefore have no physical reality.

Meaning of ''X'', ''Y'' and ''Z''

In the CIE 1931 model, ''Y'' is the luminance, ''Z'' is quasi-equal to blue (of CIE RGB), and ''X'' is a mix of the three CIE RGB curves chosen to be nonnegative (see ). Setting ''Y'' as luminance has the useful result that for any given ''Y'' value, the XZ plane will contain all possible chromaticities at that luminance.

The unit of the tristimulus values , , and is often arbitrarily chosen so that or is the brightest white that a color display supports. In this case, the Y value is known as the relative luminance. The corresponding whitepoint values for and can then be inferred using the standard illuminants.

Since the XYZ values are defined much earlier than the characterization of cone cells in the 1950s (by Ragnar Granit), the physiological meaning of these values were known only much later. The Hunt-Pointer-Estevez matrix from the 1980s relates XYZ with LMS. When inverted, it shows how the three cone responses add up to XYZ functions:

:$\begin X\\Y\\Z \end = \begin 1.91020 & -1.11212 & 0.20191 \\ 0.37095 & 0.62905 & 0 \\ 0 & 0 & 1 \end \begin L\\M\\S \end_$

In other words, the Z value is solely made up of the S cone response, the Y value a mix of L and M responses, and X value a mix of all three. This fact makes XYZ values analogous to, but different from, the LMS cone responses of the human eye.

CIE rg chromaticity space

In geometrical terms, choosing the new color space amounts to choosing a new triangle in ''rg'' chromaticity space. In the figure above-right, the ''rg'' chromaticity coordinates are shown on the two axes in black, along with the gamut of the 1931 standard observer. Shown in red are the CIE ''xy'' chromaticity axes which were determined by the above requirements. The requirement that the XYZ coordinates be non-negative means that the triangle formed by C_r, C_g, C_b must encompass the entire gamut of the standard observer. The line connecting C_r and C_b is fixed by the requirement that the $\overline(\lambda)$ function be equal to the luminance function. This line is the line of zero luminance, and is called the alychne. The requirement that the $\overline(\lambda)$ function be zero above means that the line connecting C_g and C_r must be tangent to the gamut in the region of K_r. This defines the location of point C_r. The requirement that the equal energy point be defined by puts a restriction on the line joining C_b and C_g, and finally, the requirement that the gamut fill the space puts a second restriction on this line to be very close to the gamut in the green region, which specifies the location of C_g and C_b. The above described transformation is a linear transformation from the CIE RGB space to XYZ space. The standardized transformation settled upon by the CIE special commission was as follows:

The CIE RGB space can be used to define chromaticity in the usual way: The chromaticity coordinates are ''r'', ''g'' and ''b'' where:
:\begin
r &= \frac, \\ mug &= \frac, \\ mub &= \frac.
\end

The numbers in the conversion matrix below are exact, with the number of digits specified in CIE standards.
:\begin
\begin X \\ Y \\ Z \end
&=
\begin
b_ & b_ & b_ \\
b_ & b_ & b_ \\
b_ & b_ & b_
\end
\begin R \\ G \\ B \end
\\ 0mu&=
\begin
0.490\,00 & 0.310\,00 & 0.200\,00 \\
0.176\,97 & 0.812\,40 & 0.010\,63 \\
0.000\,00 & 0.010\,00 & 0.990\,00
\end
\begin R \\ G \\ B \end
\end

The above matrix is balanced for the equi-energy stimulus: it has coordinates (1,1,1) in both RGB and XYZ coordinates.

While the above matrix is exactly specified in standards, the inverse is left unspecified so that it can be approximated to machine precision to reduce round-trip rounding errors. Its values can be computed precisely using rational numbers:

:$\begin R \\ G \\ B \end = \frac \begin 8041697 & -3049000 & -1591847 \\ -1752003 & 4851000 & 301853 \\ 17697 & -49000 & 3432153 \end \begin X \\ Y \\ Z \end$

Which has these approximate values:
:$\begin R \\ G \\ B \end \approx \begin 2.364\,61385 & -0.896\,54057 & -0.468\,07328 \\ -0.515\,16621 & 1.426\,4081 & 0.088\,7581 \\ 0.005\,2037 & -0.014\,40816 & 1.009\,20446 \end \begin X \\ Y \\ Z \end$

The XYZ primaries will have XYZ coordinates ,0,0 ,1,0 and ,0,1in XYZ space, so the columns of the inverse matrix above specify the XYZ primaries ( Cr, Cg and Cb) in RGB space. Dividing each column by its sum will give the coordinates of the XYZ primaries in rgb space which yields:

:Cr =
:Cg =
:Cb =

The r and g coordinates of the XYZ primaries are indicated in the rg chromaticity space diagram above.

The integrals of the XYZ color matching functions must all be equal by requirement 3 above, and this is set by the integral of the photopic luminous efficiency function by requirement 2 above. The tabulated sensitivity curves have a certain amount of arbitrariness in them. The shapes of the individual ''X'', ''Y'' and ''Z'' sensitivity curves can be measured with a reasonable accuracy. However, the overall luminosity curve (which in fact is a weighted sum of these three curves) is subjective, since it involves asking a test person whether two light sources have the same brightness, even if they are in completely different colors. Along the same lines, the relative magnitudes of the ''X'', ''Y'', and ''Z'' curves are arbitrary. Furthermore, one could define a valid color space with an ''X'' sensitivity curve that has twice the amplitude. This new color space would have a different shape. The sensitivity curves in the CIE 1931 and 1964 XYZ color spaces are scaled to have equal areas under the curves.

CIE xyY color space

Three dimensional color can be divided into two parts: brightness and chromaticity. For example, the color white is a bright color, while the color grey is considered to be a less bright version of that same white. In other words, the chromaticity of white and grey are the same while their brightness differs. The CIE xyY color space was deliberately designed so that the ''Y'' parameter is also a measure of the luminance of a color. The chromaticity is then specified by the two derived parameters ''x'' and ''y'', two of the three normalized values derived from the tristimulus values ''X'', ''Y'', and ''Z'':
:\begin
x &= \frac \\ muy &= \frac \\ muz &= \frac = 1 - x - y
\end

That is, because each tristimulus parameter, ''X'', ''Y'', ''Z'', is divided by the sum of all three, the resulting values, ''x'', ''y'', ''z'', each represent a proportion of the whole and so their sum must be equal to one. Therefore, the value ''z'' can be deduced by knowing ''x'' and ''y'', and consequently the latter two values are sufficient for describing the chromaticity of any color.

The derived color space specified by ''x'', ''y'', and ''Y'' is known as the CIE xyY color space and is widely used to specify colors in practice.

The ''X'' and ''Z'' tristimulus values can be calculated back from the chromaticity values ''x'' and ''y'' and the ''Y'' tristimulus value:

:\begin
X &= \fracx, \\ muZ &= \frac(1 - x - y).
\end

Mathematically the colors of the chromaticity diagram occupy a region of the real projective plane.

The figures on the right show the related chromaticity diagram. The outer curved boundary is the ''spectral locus'', with wavelengths shown in nanometers. The chromaticity diagram is a tool to specify the quality of a color regardless of its brightness. For examples,

grey has the same chromaticity as white, and teal has the same chromaticity as cyan, because the only difference between them is their brightness, not their spectral purity.

The chromaticity diagram illustrates a number of interesting properties of the CIE XYZ color space:
* The diagram represents all of the chromaticities visible to the average person. These are shown in color and this region is called the gamut of human vision. The gamut of all visible chromaticities on the CIE plot is the tongue-shaped or horseshoe-shaped figure shown in color. The curved edge of the gamut is called the ''spectral locus'' and corresponds to monochromatic light (each point representing a pure hue of a single wavelength), with wavelengths listed in nanometers. The straight edge on the lower part of the gamut is called the line of purples. These colors, although they are on the border of the gamut, have no counterpart in monochromatic light. Less saturated colors appear in the interior of the figure with white at the center.
* It is seen that all visible chromaticities correspond to non-negative values of ''x'', ''y'', and ''z'' (and therefore to non-negative values of ''X'', ''Y'', and ''Z'').
* If one chooses any two points of color on the chromaticity diagram, then all the colors that lie in a straight line between the two points can be formed by mixing these two colors. It follows that the gamut of colors must be convex in shape. All colors that can be formed by mixing three sources are found inside the triangle formed by the source points on the chromaticity diagram (and so on for multiple sources).
* An equal, additive mixture of two colors will not generally lie on the midpoint of that line segment, unless the sum of the X, Y, and Z values of one color is equal to the sum of the X, Y, and Z values of the other color (that is, both colors lie in the same plane of the type
X + Y + Z = n).
* A distance on the CIE xy chromaticity diagram does not correspond to the perceived difference between two colors. In the early 1940s, David MacAdam studied the nature of visual sensitivity to color differences, and summarized his results in the concept of a MacAdam ellipse. Based on the work of MacAdam, the CIE 1960, CIE 1964, and CIE 1976 color spaces were developed, with the goal of achieving perceptual uniformity (have an equal distance in the color space correspond to equal differences in color). Although they were a distinct improvement over the CIE 1931 system, they were not completely free of distortion.
* It can be seen that, given three real sources, these sources cannot cover the gamut of human vision. Geometrically stated, there are no three points within the gamut that form a triangle that includes the entire gamut; or more simply, the gamut of human vision is not a triangle.
* Light with a flat power spectrum in terms of wavelength (equal power in every interval) corresponds to the point ( illuminant E).

Color mixing in CIE xyY

When two or more colors are additively mixed, the x and y chromaticity coordinates of the resulting color (x_mix,y_mix) may be calculated from the chromaticities of the mixture components (x₁,y₁; x₂,y₂; …; x_n,y_n) and their corresponding luminances (L₁, L₂, …, L_n) with the following formulas:

:$x_ = \frac \quad,\quad y_ = \frac$

These formulas can be derived from the definitions of the x and y chromaticity coordinates by taking advantage of the fact that XYZ (tristimulus) values are additive. In place of the luminance values L₁, L₂, etc., one can use any photometric quantity proportional to the tristimulus value Y (including, of course, Y itself) in the context of interest; this also applies to the following mixing ratio computation.

As previously stated, when two colors are mixed, the resulting color x_mix, y_mix lies on the straight line segment that connects them on the CIE xy chromaticity diagram. The mixing ratio of colors x₁,y₁ and x₂,y₂ that results in a given x_mix,y_mix on this line segment is given by

:$\frac = \frac = \frac$

where L₁ is the luminance of color x₁,y₁ and L₂ the luminance of color x₂,y₂. Because y_mix is unambiguously determined by x_mix and vice versa (unless x₁ = x₂ or y₁ = y₂), one is enough to compute the mixing ratio.

Computing XYZ from spectral data

Emissive case

The tristimulus values for a color with a spectral radiance ''L''_e,Ω,λ are given in terms of the standard observer by:
:\begin
X &= \int_\lambda L_(\lambda)\,\overline(\lambda)\,d\lambda, \\ muY &= \int_\lambda L_(\lambda)\,\overline(\lambda)\,d\lambda, \\ muZ &= \int_\lambda L_(\lambda)\,\overline(\lambda)\,d\lambda.
\end
where $\lambda$ is the wavelength of the equivalent monochromatic light (measured in nanometers), and customary limits of the integral are \lambda\in 80, 780/math>.

The values of ''X'', ''Y'', and ''Z'' are bounded if the radiance spectrum ''L''_e,Ω,λ is bounded.

Reflective and transmissive cases

The reflective and transmissive cases are very similar to the emissive case, with a few differences. The spectral radiance ''L''_e,Ω,λ is replaced by the spectral reflectance (or transmittance) ''S(λ)'' of the object being measured, multiplied by the spectral power distribution of the illuminant ''I(λ)''.

:\begin
X &= \frac\int_\lambda S(\lambda)\,I(\lambda)\,\overline(\lambda)\,d\lambda, \\ muY &= \frac\int_\lambda S(\lambda)\,I(\lambda)\,\overline(\lambda)\,d\lambda, \\ muZ &= \frac\int_\lambda S(\lambda)\,I(\lambda)\,\overline(\lambda)\,d\lambda,
\end
where
:$N = \int_\lambda I(\lambda)\,\overline(\lambda)\,d\lambda,$

''K'' is a scaling factor (usually 1 or 100), and $\lambda$ is the wavelength of the equivalent monochromatic light (measured in nanometers), and the standard limits of the integral are \lambda\in 80, 780/math>.

Subsequent refinements

A few other XYZ-style color-matching functions have been available, correcting for known issues in the original 1931 color space. These functions imply their own XYZ-like and xyY-like color spaces.

10° standard observer

An alternative to the original 2° standard observer was defined in 1964, focusing on larger 10° stimuli. It was derived from the work of Stiles and Burch, and Speranskaya. For the 10° experiments, the observers were instructed to ignore the central 2° spot. The 1964 ''supplementary standard observer'' function is recommended when dealing with more than about a 4° field of view, but some prefer to use it always as "human wide field color discrimination is about 2 to 3 times more accurate than foveal color discrimination". The color matching functions for both standard observers are published by the CIE, who also publishes the data openly for the 2° and 10° standard observer functions. The data are discretized at wavelength intervals from to .

Analytical approximation

Table lookup can become impractical for some computational tasks. Instead of referring to the published table, the CIE XYZ color matching functions can be approximated by a sum of Gaussian functions, as follows:

Let ''g''(''x'') denote a piecewise-Gaussian function, defined by

:
g(x; \mu, \tau_1, \tau_2) = \begin
\exp \bigl(\bigr), &x < \mu, \\ mu\exp \bigl(\bigr), &x \geq \mu.
\end

That is, ''g''(''x'') resembles a bell curve with its peak at , a spread/standard deviation of $1/\tau_1$ to the left of the mean, and spread of $1/\tau_2$ to the right of the mean. With the wavelength ''λ'' measured in nanometers, we then approximate the 1931 color matching functions:

:
\begin
\overline(\lambda) &= 1.056\,g(\lambda; 599.8, 0.0264, 0.0323) + 0.362\,g(\lambda; 442.0, 0.0624, 0.0374) \\ mu&\quad - 0.065\,g(\lambda; 501.1, 0.0490, 0.0382), \\ mu\overline(\lambda) &= 0.821\,g(\lambda; 568.8, 0.0213, 0.0247) + 0.286\,g(\lambda; 530.9, 0.0613, 0.0322), \\ mu\overline(\lambda) &= 1.217\,g(\lambda; 437.0, 0.0845, 0.0278) + 0.681\,g(\lambda; 459.0, 0.0385, 0.0725).
\end

The squared differences between the above approximation and the measured CIE ''xyz'' color matching functions is less than the within-observer variance encountered in the experimental measurements used to form the CIE standards. It is also possible to use fewer Gaussian functions, with one Gaussian for each "lobe". CIE 1964 fits well with a one-lobe function.

The CIE XYZ color matching functions are nonnegative, and lead to nonnegative XYZ coordinates for all real colors (that is, for nonnegative light spectra). Other observers, such as for the CIE RGB space or other RGB color spaces, are defined by other sets of three color-matching functions, not generally nonnegative, and lead to tristimulus values in those other spaces, which may include negative coordinates for some real colors.

Others

; Judd and Vos corrections for the 2° CMF
: The most serious problem with the 1931 CIE XYZ color matching functions is the error in the photopic Y (or $V(\lambda)$ function on the blue end of the spectrum. The Judd (1951) and its following Vos (1978) corrections sought to correct for the issue without deviating from the original methodology.
; CIE 1964 X₁₀Y₁₀Z₁₀
: X₁₀Y₁₀Z₁₀ (also written XYZ₁₀ and analogously for the following) is the XYZ-style color space defined using the CIE 1964 10° observer CMFs. The 3 CMFs are mainly derived from Stiles and Burch's RGB color-matching functions, which unlike the Wright–Guild functions (and the subsequent Judd–Vos corrections) are "directly measured", freeing them from the reconstruction errors of the 1931 functions.
: Stiles and Burch also published a set of 2° RGB color-matching functions; however, no XYZ space derived from them has been formally recognized by the CIE.
; CIE 170-2 X_FY_FZ_F
: X_FY_FZ_F is the XYZ-style color space defined using the Stockman & Sharpe (2000) physiological 2° observer, which is in turn a linear combination of the LMS cone response functions. The CMF data, along with the physiological 10° dataset, is available from the Colour & Vision Research laboratory of University College London down to 0.1 nm resolution.
; CIE 170-2 X_F,10Y_F,10Z_F,10
: This space is based on the Stockman & Sharpe (2000) physiological 10° observer.

According to Konica Minolta, the older CIE 1931 CMF exhibits metamerism failure (failure to predict when colors appear the same) for wide color gamut displays containing narrowband emitters like OLED, whereas the 2015 XYZ_F CMF is not affected. Older Sony manuals recommend using the Judd-Vos correction by applying an offset to the white point depending on the display technology used.

See also

* Trichromacy
* Impossible color
* CIELAB color space
* Standard illuminant, the definition of white point used by CIE and commonly shown in color space diagrams as E, D50 or D65

References

Further reading

*
*
* (originally published by the Society of Dyers and Colourists, Bradford, 1981.)

External links

Introduction to Colour Science
William Andrew Steer.


an
Delphi source

CIE Color Space
Gernot Hoffmann


Andrew Stockman and Lindsay T. Sharpe.

Calculation from the original experimental data of the CIE 1931 RGB standard observer spectral chromaticity co-ordinates and color matching functions


MATLAB toolbox for color science computation and accurate color reproduction (by Jesus Malo and Maria Jose Luque, Universitat de Valencia). It includes CIE standard tristimulus colorimetry and transformations to a number of non-linear color appearance models (CIE Lab, CIE CAM, etc.).

A Look at the Past and Future of LED Binning

Measuring Color in a world of light

{{DEFAULTSORT:Cie 1931 Color Space
Color space
1931 introductions
Articles with example C code