|
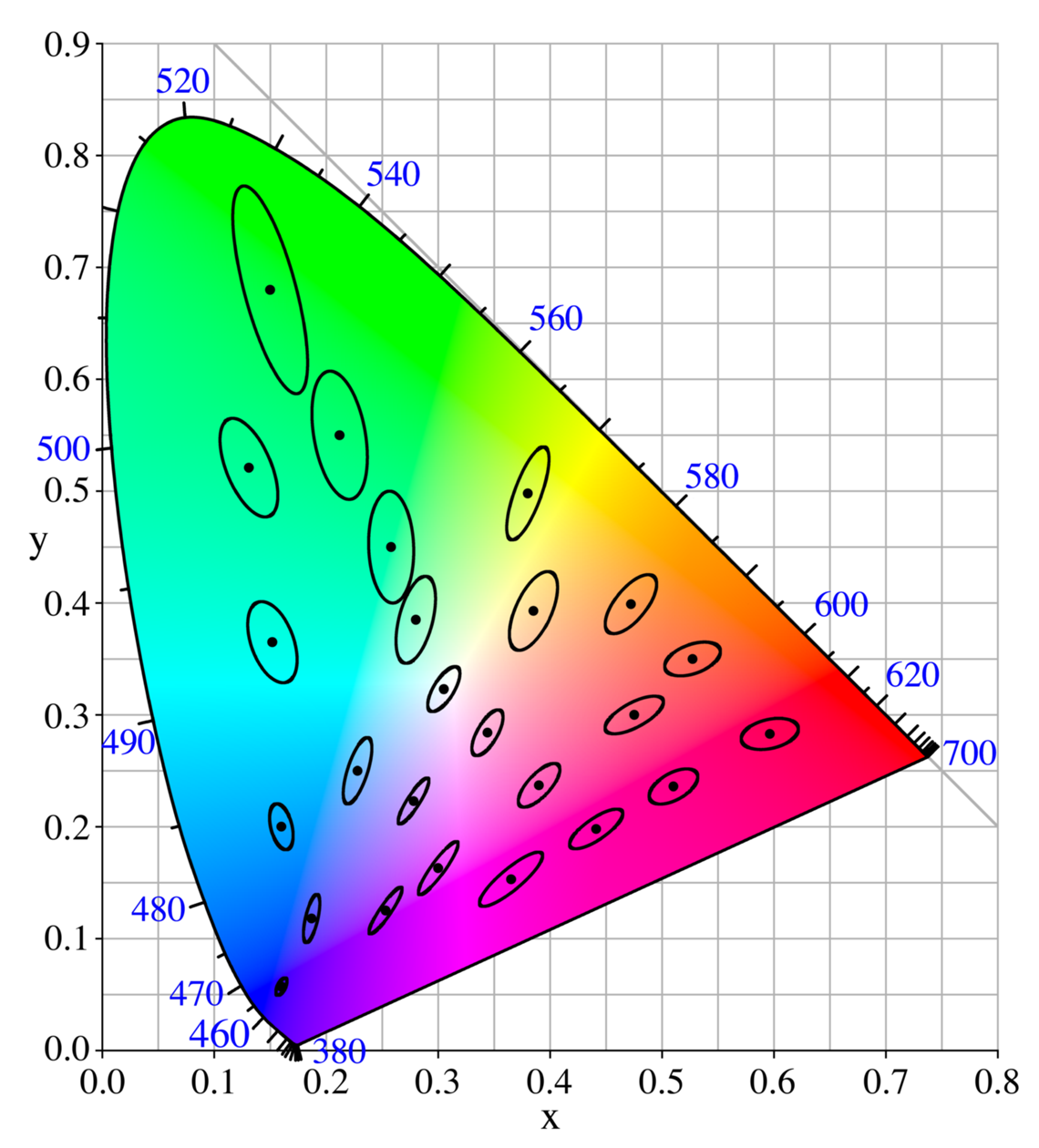
MacAdam Ellipse
In the study of color vision, a MacAdam ellipse is roughly a region on a chromaticity diagram which contains all colors which are indistinguishable to the average human eye, from the color at the center of the ellipse. Specifically, it is the standard deviation of a number of experimental color matches to the central color. Assuming a Multivariate normal distribution, bivariate normal distribution of these match points, a MacAdam ellipse thus contains about 39% of the color match points. A 2X MacAdam ellipse will contain about 86% of the match points, and a 3X MacAdam ellipse will contain about 99% of the match points. The just-noticeable differences of chromaticity is generally taken to be a 3X MacAdam ellipse. Standard Deviation Color Matching in LED lighting uses deviations relative to MacAdam ellipses to describe color precision of a light source. History In the study of color perception, it is essential to develop a method of specifying a particular color such that it ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Color Vision
Color vision, a feature of visual perception, is an ability to perceive differences between light composed of different frequencies independently of light intensity. Color perception is a part of the larger visual system and is mediated by a complex process between neurons that begins with differential stimulation of different types of photoreceptors by light entering the eye. Those photoreceptors then emit outputs that are propagated through many layers of neurons ultimately leading to higher cognitive functions in the brain. Color vision is found in many animals and is mediated by similar underlying mechanisms with common types of biological molecules and a complex history of the evolution of color vision within different animal taxa. In primates, color vision may have evolved under selective pressure for a variety of visual tasks including the foraging for nutritious young leaves, ripe fruit, and flowers, as well as detecting predator camouflage and emotional states in othe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Luminance
Luminance is a photometric measure of the luminous intensity per unit area of light travelling in a given direction. It describes the amount of light that passes through, is emitted from, or is reflected from a particular area, and falls within a given solid angle. The procedure for conversion from spectral radiance to luminance is standardized by the CIE and ISO. Brightness is the term for the ''subjective'' impression of the ''objective'' luminance measurement standard (see for the importance of this contrast). The SI unit for luminance is candela per square metre (cd/m2). A non-SI term for the same unit is the nit. The unit in the Centimetre–gram–second system of units (CGS) (which predated the SI system) is the stilb, which is equal to one candela per square centimetre or 10 kcd/m2. Description Luminance is often used to characterize emission or reflection from flat, diffuse surfaces. Luminance levels indicate how much luminous power could be det ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mahalanobis Distance
The Mahalanobis distance is a distance measure, measure of the distance between a point P and a probability distribution D, introduced by Prasanta Chandra Mahalanobis, P. C. Mahalanobis in 1936. The mathematical details of Mahalanobis distance first appeared in the ''Journal of The Asiatic Society of Bengal'' in 1936. Mahalanobis's definition was prompted by the problem of similarity measure, identifying the similarities of skulls based on measurements (the earliest work related to similarities of skulls are from 1922 and another later work is from 1927). Raj Chandra Bose, R.C. Bose later obtained the sampling distribution of Mahalanobis distance, under the assumption of equal dispersion. It is a multivariate generalization of the square of the standard score z=(x- \mu)/\sigma: how many standard deviations away P is from the mean of D. This distance is zero for P at the mean of D and grows as P moves away from the mean along each principal component axis. If each of these axes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tissot's Indicatrix
In cartography, a Tissot's indicatrix (Tissot indicatrix, Tissot's ellipse, Tissot ellipse, ellipse of distortion) (plural: "Tissot's indicatrices") is a mathematical contrivance presented by French mathematician Nicolas Auguste Tissot in 1859 and 1871 in order to characterize local distortions due to map projection. It is the geometry that results from Projection (linear algebra), projecting a circle of infinitesimal radius from a curved geometric model, such as a globe, onto a map. Tissot proved that the resulting diagram is an ellipse whose axes indicate the two Principal curvature, principal directions along which scale is maximal and minimal at that point on the map. A single indicatrix describes the distortion at a single point. Because distortion varies across a map, generally Tissot's indicatrices are placed across a map to illustrate the spatial change in distortion. A common scheme places them at each intersection of displayed meridians and parallels. These schematics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Tensor
In the mathematical field of differential geometry, a metric tensor (or simply metric) is an additional structure on a manifold (such as a surface) that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point of is a bilinear form defined on the tangent space at (that is, a bilinear function that maps pairs of tangent vectors to real numbers), and a metric field on consists of a metric tensor at each point of that varies smoothly with . A metric tensor is ''positive-definite'' if for every nonzero vector . A manifold equipped with a positive-definite metric tensor is known as a Riemannian manifold. Such a metric tensor can be thought of as specifying ''infinitesimal'' distance on the manifold. On a Riemannian manifold , the length of a smooth curve between two points and can be defined by integration, and the distance between and can be defined as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
LMS Color Space
LMS (long, medium, short), is a color space which represents the response of the three types of Cone cell, cones of the human eye, named for their responsivity (sensitivity) peaks at long, medium, and short wavelengths. The numerical range is generally not specified, except that the lower end is generally bounded by zero. It is common to use the LMS color space when performing chromatic adaptation (estimating the appearance of a sample under a different illuminant). It is also useful in the study of color blindness, when one or more cone types are defective. Definition The cone response functions \bar(\lambda), \bar(\lambda),\bar(\lambda) are the color matching functions (CMFs) for the LMS color space. The chromaticity coordinates (L, M, S) for a spectral distribution J(\lambda) are defined as: : L = \int^\infty_0 J(\lambda)\bar(\lambda)d\lambda : M = \int^\infty_0 J(\lambda)\bar(\lambda)d\lambda : S = \int^\infty_0 J(\lambda)\bar(\lambda)d\lambda The cone response function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisher Information Metric
In information geometry, the Fisher information metric is a particular Riemannian metric which can be defined on a smooth statistical manifold, ''i.e.'', a smooth manifold whose points are probability distributions. It can be used to calculate the distance between probability distributions. The metric is interesting in several aspects. By Chentsov’s theorem, the Fisher information metric on statistical models is the only Riemannian metric (up to rescaling) that is invariant under sufficient statistics. It can also be understood to be the infinitesimal form of the relative entropy (''i.e.'', the Kullback–Leibler divergence); specifically, it is the Hessian matrix, Hessian of the divergence. Alternately, it can be understood as the metric induced by the flat space Euclidean metric, after appropriate changes of variable. When extended to complex projective Hilbert space, it becomes the Fubini–Study metric; when written in terms of mixed state (physics), mixed states, it is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CIELAB
The CIELAB color space, also referred to as ''L*a*b*'', is a color space defined by the International Commission on Illumination (abbreviated CIE) in 1976. It expresses color as three values: ''L*'' for perceptual lightness and ''a*'' and ''b*'' for the four Unique hues, unique colors of human vision: red, green, blue and yellow. CIELAB was intended as a perceptually uniform space, where a given numerical change corresponds to a similar perceived change in color. While the LAB space is not truly perceptually uniform, it nevertheless is useful in industry for detecting small differences in color. Like the CIE 1931 color space, CIEXYZ space it derives from, CIELAB color space is a device-independent, "standard observer" model. The colors it defines are not relative to any particular device such as a computer monitor or a printer, but instead relate to the CIE 1931 color space#CIE standard observer, CIE standard observer which is an averaging of the results of color matching expe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CIELUV
In colorimetry, the CIE 1976 ''L''*, ''u''*, ''v''* color space, commonly known by its abbreviation CIELUV, is a color space adopted by the International Commission on Illumination (CIE) in 1976, as a simple-to-compute transformation of the 1931 CIE XYZ color space, but which attempted perceptual uniformity. It is extensively used for applications such as computer graphics which deal with colored lights. Although additive mixtures of different colored lights will fall on a line in CIELUV's uniform chromaticity diagram (called the ''CIE 1976 UCS''), such additive mixtures will not, contrary to popular belief, fall along a line in the CIELUV color space unless the mixtures are constant in lightness. Historical background CIELUV is an Adams chromatic valence color space and is an update of the CIE 1964 (''U''*, ''V''*, ''W''*) color space (CIEUVW). The differences include a slightly modified lightness scale and a modified uniform chromaticity scale, in which one of the coordina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric (mathematics)
In mathematics, a metric space is a set together with a notion of ''distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are a general setting for studying many of the concepts of mathematical analysis and geometry. The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another. Since they are very general, metric spaces are a tool used in many different branches of mathematics. Many types of mathematical objects have a natural notion of distance and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Colour Difference
In color science, color difference or color distance is the separation between two colors. This metric allows quantified examination of a notion that formerly could only be described with adjectives. Quantification of these properties is of great importance to those whose work is color-critical. Common definitions make use of the Euclidean distance in a device-independent color space. Euclidean sRGB As most definitions of color difference are distances within a color space, the standard means of determining distances is the Euclidean distance. If one presently has an RGB (red, green, blue) tuple and wishes to find the color difference, computationally one of the easiest is to consider ''R'', ''G'', ''B'' linear dimensions defining the color space. A very simple example can be given between the two colors with RGB values (0, 64, 0) () and (255, 64, 0) (): their distance is 255. Going from there to (255, 64, 128) () is a distance of 128. When we wish to calculate distance from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ACM Transactions On Graphics
''ACM Transactions on Graphics'' (TOG) is a bimonthly peer-reviewed scientific journal that covers the field of computer graphics. The editor-in-chief is Carol O'Sullivan (Trinity College Dublin). According to the ''Journal Citation Reports'', the journal had a 2023 impact factor of 7.8. The journal ranks 1st in computer graphics publications, according to Google Scholar Metrics. History It was established in 1982 and is published by the Association for Computing Machinery. TOG publishes two special issues for ACM SIGGRAPH's conference proceedings. Starting in 2003, all papers accepted for presentation at the annual SIGGRAPH SIGGRAPH (Special Interest Group on Computer Graphics and Interactive Techniques) is an annual conference centered around computer graphics organized by ACM, starting in 1974 in Boulder, CO. The main conference has always been held in North ... conference are printed in a special summer issue of the journal. Beginning in 2008, papers presented at S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |