Bregman Divergence on:
[Wikipedia]
[Google]
[Amazon]
In
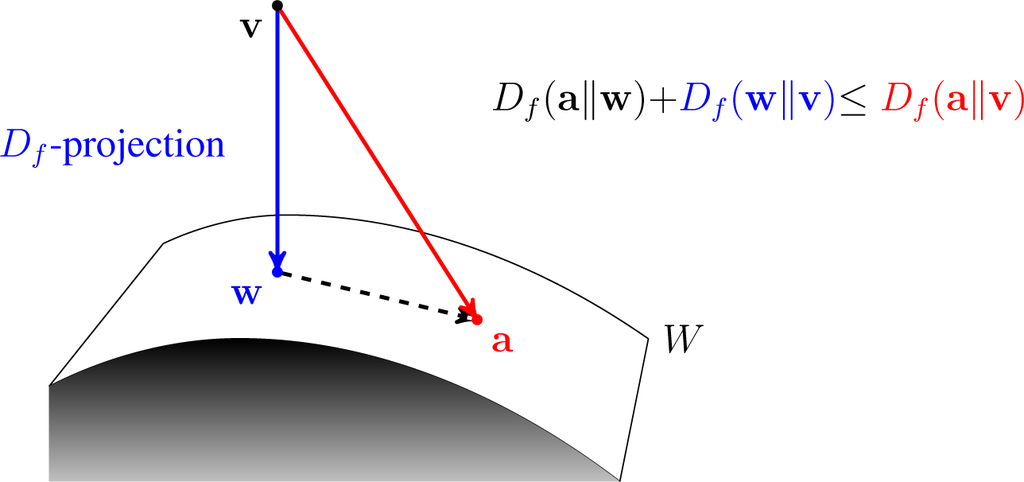 * Bregman projection: For any , define the "Bregman projection" of onto :
. Then
** if is convex, then the projection is unique if it exists;
** if is nonempty, closed, and convex and is finite dimensional, then the projection exists and is unique.
* Generalized Pythagorean Theorem:
For any ,
This is an equality if is in the relative interior of .
In particular, this always happens when is an affine set.
* ''Lack'' of triangle inequality: Since the Bregman divergence is essentially a generalization of squared Euclidean distance, there is no triangle inequality. Indeed, , which may be positive or negative.
* Bregman projection: For any , define the "Bregman projection" of onto :
. Then
** if is convex, then the projection is unique if it exists;
** if is nonempty, closed, and convex and is finite dimensional, then the projection exists and is unique.
* Generalized Pythagorean Theorem:
For any ,
This is an equality if is in the relative interior of .
In particular, this always happens when is an affine set.
* ''Lack'' of triangle inequality: Since the Bregman divergence is essentially a generalization of squared Euclidean distance, there is no triangle inequality. Indeed, , which may be positive or negative.
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, specifically statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
and information geometry
Information geometry is an interdisciplinary field that applies the techniques of differential geometry to study probability theory and statistics. It studies statistical manifolds, which are Riemannian manifolds whose points correspond to proba ...
, a Bregman divergence or Bregman distance is a measure of difference between two points, defined in terms of a strictly convex function
In mathematics, a real-valued function is called convex if the line segment between any two distinct points on the graph of a function, graph of the function lies above or on the graph between the two points. Equivalently, a function is conve ...
; they form an important class of divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the rate that the vector field alters the volume in an infinitesimal neighborhood of each point. (In 2D this "volume" refers to ...
s. When the points are interpreted as probability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
s – notably as either values of the parameter of a parametric model
In statistics, a parametric model or parametric family or finite-dimensional model is a particular class of statistical models. Specifically, a parametric model is a family of probability distributions that has a finite number of parameters.
Defi ...
or as a data set of observed values – the resulting distance is a statistical distance. The most basic Bregman divergence is the squared Euclidean distance.
Bregman divergences are similar to metrics, but satisfy neither the triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side.
This statement permits the inclusion of Degeneracy (mathematics)#T ...
(ever) nor symmetry (in general). However, they satisfy a generalization of the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
, and in information geometry
Information geometry is an interdisciplinary field that applies the techniques of differential geometry to study probability theory and statistics. It studies statistical manifolds, which are Riemannian manifolds whose points correspond to proba ...
the corresponding statistical manifold is interpreted as a (dually) flat manifold. This allows many techniques of optimization theory to be generalized to Bregman divergences, geometrically as generalizations of least squares.
Bregman divergences are named after Russian mathematician Lev M. Bregman, who introduced the concept in 1967.
Definition
Let be a continuously-differentiable, strictlyconvex function
In mathematics, a real-valued function is called convex if the line segment between any two distinct points on the graph of a function, graph of the function lies above or on the graph between the two points. Equivalently, a function is conve ...
defined on a convex set
In geometry, a set of points is convex if it contains every line segment between two points in the set.
For example, a solid cube (geometry), cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is n ...
.
The Bregman distance associated with ''F'' for points is the difference between the value of ''F'' at point ''p'' and the value of the first-order Taylor expansion of ''F'' around point ''q'' evaluated at point ''p'':
:
Properties
* Non-negativity: for all , . This is a consequence of the convexity of . * Positivity: When is strictly convex, iff . * Uniqueness up to affine difference: iff is an affine function. * Convexity: is convex in its first argument, but not necessarily in the second argument. If F is strictly convex, then is strictly convex in its first argument. ** For example, Take f(x) = , x, , smooth it at 0, then take , then . * Linearity: If we think of the Bregman distance as an operator on the function ''F'', then it is linear with respect to non-negative coefficients. In other words, for strictly convex and differentiable, and , :: * Duality: If F is strictly convex, then the function F has aconvex conjugate
In mathematics and mathematical optimization, the convex conjugate of a function is a generalization of the Legendre transformation which applies to non-convex functions. It is also known as Legendre–Fenchel transformation, Fenchel transformati ...
which is also strictly convex and continuously differentiable on some convex set . The Bregman distance defined with respect to is dual to as
::
:Here, and are the dual points corresponding to p and q.
:Moreover, using the same notations :
::
* Integral form: by the integral remainder form of Taylor's Theorem, a Bregman divergence can be written as the integral of the Hessian of along the line segment between the Bregman divergence's arguments.
* Mean as minimizer: A key result about Bregman divergences is that, given a random vector, the mean vector minimizes the expected Bregman divergence from the random vector. This result generalizes the textbook result that the mean of a set minimizes total squared error to elements in the set. This result was proved for the vector case by (Banerjee et al. 2005), and extended to the case of functions/distributions by (Frigyik et al. 2008). This result is important because it further justifies using a mean as a representative of a random set, particularly in Bayesian estimation.
* Bregman balls are bounded, and compact if X is closed: Define Bregman ball centered at x with radius r by . When is finite dimensional, , if is in the relative interior of , or if is locally closed at (that is, there exists a closed ball centered at , such that is closed), then is bounded for all . If is closed, then is compact for all .
* Law of cosines:
For any
::
* Parallelogram law
In mathematics, the simplest form of the parallelogram law (also called the parallelogram identity) belongs to elementary geometry. It states that the sum of the squares of the lengths of the four sides of a parallelogram equals the sum of the s ...
: for any ,
 * Bregman projection: For any , define the "Bregman projection" of onto :
. Then
** if is convex, then the projection is unique if it exists;
** if is nonempty, closed, and convex and is finite dimensional, then the projection exists and is unique.
* Generalized Pythagorean Theorem:
For any ,
This is an equality if is in the relative interior of .
In particular, this always happens when is an affine set.
* ''Lack'' of triangle inequality: Since the Bregman divergence is essentially a generalization of squared Euclidean distance, there is no triangle inequality. Indeed, , which may be positive or negative.
* Bregman projection: For any , define the "Bregman projection" of onto :
. Then
** if is convex, then the projection is unique if it exists;
** if is nonempty, closed, and convex and is finite dimensional, then the projection exists and is unique.
* Generalized Pythagorean Theorem:
For any ,
This is an equality if is in the relative interior of .
In particular, this always happens when is an affine set.
* ''Lack'' of triangle inequality: Since the Bregman divergence is essentially a generalization of squared Euclidean distance, there is no triangle inequality. Indeed, , which may be positive or negative.
Proofs
* Non-negativity and positivity: use Jensen's inequality. * Uniqueness up to affine difference: Fix some , then for any other , we have by definition. * Convexity in the first argument: by definition, and use convexity of F. Same for strict convexity. * Linearity in F, law of cosines, parallelogram law: by definition. * Duality: See figure 1 of. * Bregman balls are bounded, and compact if X is closed: Fix . Take affine transform on , so that . Take some , such that . Then consider the "radial-directional" derivative of on the Euclidean sphere . for all . Since is compact, it achieves minimal value at some . Since is strictly convex, . Then . Since is in , is continuous in , thus is closed if is. * Projection is well-defined when is closed and convex. Fix . Take some , then let . Then draw the Bregman ball . It is closed and bounded, thus compact. Since is continuous and strictly convex on it, and bounded below by , it achieves a unique minimum on it. * Pythagorean inequality. By cosine law, , which must be , since minimizes in , and is convex. * Pythagorean equality when is in the relative interior of . If , then since is in the relative interior, we can move from in the direction opposite of , to decrease , contradiction. Thus .Classification theorems
* The only symmetric Bregman divergences on are squared generalized Euclidean distances (Mahalanobis distance
The Mahalanobis distance is a distance measure, measure of the distance between a point P and a probability distribution D, introduced by Prasanta Chandra Mahalanobis, P. C. Mahalanobis in 1936. The mathematical details of Mahalanobis distance ...
), that is, for some positive definite .
The following two characterizations are for divergences on , the set of all probability measures on , with .
Define a divergence on as any function of type