Betti number

In algebraic topology, the Betti numbers are used to distinguish topological spaces based on the connectivity of ''n''-dimensional simplicial complexes. For the most reasonable finite-dimensional spaces (such as compact manifolds, finite simplicial complexes or CW complexes), the sequence of Betti numbers is 0 from some point onward (Betti numbers vanish above the dimension of a space), and they are all finite.

The ''n''th Betti number represents the rank of the ''n''th homology group, denoted ''H''_''n'', which tells us the maximum number of cuts that can be made before separating a surface into two pieces or 0-cycles, 1-cycles, etc. For example, if $H_n(X) \cong 0$ then $b_n(X) = 0$, if $H_n(X) \cong \mathbb$ then $b_n(X) = 1$, if $H_n(X) \cong \mathbb \oplus \mathbb$ then $b_n(X) = 2$, if $H_n(X) \cong \mathbb \oplus \mathbb\oplus \mathbb$ then $b_n(X) = 3$, etc. Note that only the ranks of infinite groups are considered, so for example if $H_n(X) \cong \mathbb^k \oplus \mathbb/(2)$, where $\mathbb/(2)$ is the finite cyclic group of order 2, then $b_n(X) = k$. These finite components of the homology groups are their torsion subgroups, and they are denoted by torsion coefficients.

The term "Betti number" was coined by Henri Poincaré after Enrico Betti. The modern formulation is due to Emmy Noether. Betti numbers are used today in fields such as simplicial homology, computer science and digital images.

Geometric interpretation

Informally, the ''k''th Betti number refers to the number of ''k''-dimensional ''holes'' on a topological surface. A "''k''-dimensional ''hole''" is a ''k''-dimensional cycle that is not a boundary of a (''k''+1)-dimensional object.

The first few Betti numbers have the following definitions for 0-dimensional, 1-dimensional, and 2-dimensional simplicial complexes:
* ''b''₀ is the number of connected components;
* ''b''₁ is the number of one-dimensional or "circular" holes;
* ''b''₂ is the number of two-dimensional "voids" or "cavities".

Thus, for example, a torus has one connected surface component so ''b''₀ = 1, two "circular" holes (one equatorial and one meridional) so ''b''₁ = 2, and a single cavity enclosed within the surface so ''b''₂ = 1.

Another interpretation of ''b''_k is the maximum number of ''k''-dimensional curves that can be removed while the object remains connected. For example, the torus remains connected after removing two 1-dimensional curves (equatorial and meridional) so ''b''₁ = 2.

The two-dimensional Betti numbers are easier to understand because we can see the world in 0, 1, 2, and 3-dimensions.

Formal definition

For a non-negative integer ''k'', the ''k''th Betti number ''b''_''k''(''X'') of the space ''X'' is defined as the rank (number of linearly independent generators) of the abelian group ''H''_''k''(''X''), the ''k''th homology group of ''X''. The ''k''th homology group is $H_ = \ker \delta_ / \operatorname \delta_$, the $\delta_$s are the boundary maps of the simplicial complex and the rank of H_k is the ''k''th Betti number. Equivalently, one can define it as the vector space dimension of ''H''_''k''(''X''; Q) since the homology group in this case is a vector space over Q. The universal coefficient theorem, in a very simple torsion-free case, shows that these definitions are the same.

More generally, given a field ''F'' one can define ''b''_''k''(''X'', ''F''), the ''k''th Betti number with coefficients in ''F'', as the vector space dimension of ''H''_''k''(''X'', ''F'').

Poincaré polynomial

The Poincaré polynomial of a surface is defined to be the generating function of its Betti numbers. For example, the Betti numbers of the torus are 1, 2, and 1; thus its Poincaré polynomial is $1+2x+x^2$. The same definition applies to any topological space which has a finitely generated homology.

Given a topological space which has a finitely generated homology, the Poincaré polynomial is defined as the generating function of its Betti numbers, via the polynomial where the coefficient of $x^n$ is $b_n$.

Examples

Betti numbers of a graph

Consider a topological graph ''G'' in which the set of vertices is ''V'', the set of edges is ''E'', and the set of connected components is ''C''. As explained in the page on graph homology, its homology groups are given by:
: $H_k(G) = \begin \mathbb Z^ & k=0 \\ \mathbb Z^ & k=1 \\ \ & \text \end$

This may be proved straightforwardly by mathematical induction on the number of edges. A new edge either increments the number of 1-cycles or decrements the number of connected components.

Therefore, the "zero-th" Betti number ''b''₀(''G'') equals , ''C'', , which is simply the number of connected components.

The first Betti number ''b''₁(''G'') equals , ''E'', + , ''C'', - , ''V'', . It is also called the cyclomatic number—a term introduced by Gustav Kirchhoff before Betti's paper. See cyclomatic complexity for an application to software engineering.

All other Betti numbers are 0.

Betti numbers of a simplicial complex

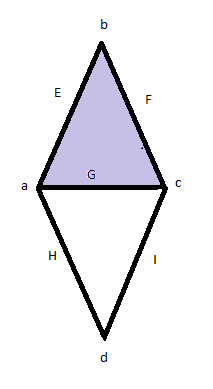
Consider a simplicial complex with 0-simplices: a, b, c, and d, 1-simplices: E, F, G, H and I, and the only 2-simplex is J, which is the shaded region in the figure. There is one connected component in this figure (''b''₀); one hole, which is the unshaded region (''b''₁); and no "voids" or "cavities" (''b''₂).

This means that the rank of $H_0$ is 1, the rank of $H_$ is 1 and the rank of $H_2$ is 0.

The Betti number sequence for this figure is 1, 1, 0, 0, ...; the Poincaré polynomial is $1 + x\,$.

Betti numbers of the projective plane

The homology groups of the projective plane ''P'' are:
: $H_k(P) = \begin \mathbb Z & k=0 \\ \mathbb Z _ 2 & k=1 \\ \ & \text \end$

Here, Z₂ is the cyclic group of order 2. The 0-th Betti number is again 1. However, the 1-st Betti number is 0. This is because ''H''₁(''P'') is a finite group - it does not have any infinite component. The finite component of the group is called the torsion coefficient of ''P''. The (rational) Betti numbers ''b''_''k''(''X'') do not take into account any torsion in the homology groups, but they are very useful basic topological invariants. In the most intuitive terms, they allow one to count the number of ''holes'' of different dimensions.

Properties

Euler characteristic

For a finite CW-complex ''K'' we have
: $\chi(K) = \sum_^\infty(-1)^i b_i(K, F), \,$
where $\chi(K)$ denotes Euler characteristic of ''K'' and any field ''F''.

Cartesian product

For any two spaces ''X'' and ''Y'' we have
: $P_ = P_X P_Y ,$
where $P_X$ denotes the Poincaré polynomial of ''X'', (more generally, the Hilbert–Poincaré series, for infinite-dimensional spaces), i.e., the generating function of the Betti numbers of ''X'':
: $P_X(z) = b_0(X) + b_1(X)z + b_2(X)z^2 + \cdots , \,\!$
see Künneth theorem.

Symmetry

If ''X'' is ''n''-dimensional manifold, there is symmetry interchanging $k$ and $n - k$, for any $k$:
: $b_k(X) = b_(X),$
under conditions (a ''closed'' and ''oriented'' manifold); see Poincaré duality.

Different coefficients

The dependence on the field ''F'' is only through its characteristic. If the homology groups are torsion-free, the Betti numbers are independent of ''F''. The connection of ''p''-torsion and the Betti number for characteristic ''p'', for ''p'' a prime number, is given in detail by the universal coefficient theorem (based on Tor functors, but in a simple case).

More examples

# The Betti number sequence for a circle is 1, 1, 0, 0, 0, ...;
#: the Poincaré polynomial is
#:: $1 + x\,$.
# The Betti number sequence for a three-torus is 1, 3, 3, 1, 0, 0, 0, ... .
#: the Poincaré polynomial is
#:: $(1 + x)^3 = 1 + 3x + 3x^2 + x^3\,$.
# Similarly, for an ''n''-torus,
#: the Poincaré polynomial is
#:: $(1 + x)^n \,$ (by the Künneth theorem), so the Betti numbers are the binomial coefficients.

It is possible for spaces that are infinite-dimensional in an essential way to have an infinite sequence of non-zero Betti numbers. An example is the infinite-dimensional complex projective space, with sequence 1, 0, 1, 0, 1, ... that is periodic, with period length 2.
In this case the Poincaré function is not a polynomial but rather an infinite series
: $1 + x^2 + x^4 + \dotsb$,
which, being a geometric series, can be expressed as the rational function
: $\frac.$

More generally, any sequence that is periodic can be expressed as a sum of geometric series, generalizing the above. For example $a,b,c,a,b,c,\dots,$ has the generating function
: $\left(a + bx + cx^2\right)/\left(1 - x^3\right) \,$
and more generally linear recursive sequences are exactly the sequences generated by rational functions; thus the Poincaré series is expressible as a rational function if and only if the sequence of Betti numbers is a linear recursive sequence.

The Poincaré polynomials of the compact simple Lie groups are:
: $\begin P_(x) &= \left(1 + x^3\right)\left(1 + x^5\right)\cdots\left(1 + x^\right) \\ P_(x) &= \left(1 + x^3\right)\left(1 + x^7\right)\cdots\left(1 + x^\right) \\ P_(x) &= \left(1 + x^3\right)\left(1 + x^7\right)\cdots\left(1 + x^\right) \\ P_(x) &= \left(1 + x^\right)\left(1 + x^3\right)\left(1 + x^7\right)\cdots\left(1 + x^\right) \\ P_(x) &= \left(1 + x^3\right)\left(1 + x^\right) \\ P_(x) &= \left(1 + x^3\right)\left(1 + x^\right)\left(1 + x^\right)\left(1 + x^\right) \\ P_(x) &= \left(1 + x^3\right)\left(1 + x^\right)\left(1 + x^\right)\left(1 + x^\right)\left(1 + x^\right)\left(1 + x^\right) \\ P_(x) &= \left(1 + x^3\right)\left(1 + x^\right)\left(1 + x^\right)\left(1 + x^\right)\left(1 + x^\right)\left(1 + x^\right)\left(1 + x^\right) \\ P_(x) &= \left(1 + x^3\right)\left(1 + x^\right)\left(1 + x^\right)\left(1 + x^\right)\left(1 + x^\right)\left(1 + x^\right)\left(1 + x^\right)\left(1 + x^\right) \end$

Relationship with dimensions of spaces of differential forms

In geometric situations when $X$ is a closed manifold, the importance of the Betti numbers may arise from a different direction, namely that they predict the dimensions of vector spaces of closed differential forms ''modulo'' exact differential forms. The connection with the definition given above is via three basic results, de Rham's theorem and Poincaré duality (when those apply), and the universal coefficient theorem of homology theory.

There is an alternate reading, namely that the Betti numbers give the dimensions of spaces of harmonic forms. This requires the use of some of the results of Hodge theory on the Hodge Laplacian.

In this setting, Morse theory gives a set of inequalities for alternating sums of Betti numbers in terms of a corresponding alternating sum of the number of critical points $N_i$ of a Morse function of a given index:
: $b_i(X) - b_ (X) + \cdots \le N _i - N_ + \cdots.$

Edward Witten gave an explanation of these inequalities by using the Morse function to modify the exterior derivative in the de Rham complex.

See also

* Topological data analysis
* Torsion coefficient
* Euler characteristic

References

* .
* .

{{DEFAULTSORT:Betti Number
Algebraic topology
Graph invariants
Topological graph theory
Generating functions