BIO-LGCA

In computational and mathematical biology, a biological lattice-gas cellular automaton (BIO-LGCA) is a discrete model for moving and interacting biological agents, a type of cellular automaton. The BIO-LGCA is based on the lattice-gas cellular automaton (LGCA) model used in fluid dynamics. A BIO-LGCA model describes cells and other motile biological agents as point particles moving on a discrete lattice, thereby interacting with nearby particles. Contrary to classic cellular automaton models, particles in BIO-LGCA are defined by their position and velocity. This allows to model and analyze active fluids and collective migration mediated primarily through changes in momentum, rather than density. BIO-LGCA applications include cancer invasion and cancer progression.

Model definition

As are all cellular automaton models, a BIO-LGCA model is defined by a lattice $\mathcal$, a state space $\mathcal$, a neighborhood $\mathcal$, and a rule $\mathcal$.

* The lattice ($\mathcal$) defines the set of all possible particle positions. Particles are restricted to occupy only certain positions, typically resulting from a regular and periodic tesselation of space. Mathematically, $\mathcal\subset\mathbb^d$ is a discrete subset of $d$-dimensional space.
* The state space ($\mathcal$) describes the possible states of particles within every lattice site $\mathbf\in\mathcal$. In BIO-LGCA, multiple particles with different velocities may occupy a single lattice site, as opposed to classic cellular automaton models, where typically only a single cell can reside in every lattice node simultaneously. This makes the state space slightly more complex than that of classic cellular automaton models (see below).
* The neighborhood ($\mathcal$) indicates the subset of lattice sites which determines the dynamics of a given site in the lattice. Particles only interact with other particles within their neighborhood. Boundary conditions must be chosen for neighborhoods of lattice sites at the boundary of finite lattices. Neighborhoods and boundary conditions are identically defined as those for regular cellular automata (see Cellular automaton).
* The rule ($\mathcal$) dictates how particles move, proliferate, or die with time. As every cellular automaton, BIO-LGCA evolves in discrete time steps. In order to simulate the system dynamics, the rule is synchronously applied to every lattice site at every time step. Rule application changes the original state of a lattice site to a new state. The rule depends on the states of lattice sites in the interaction neighborhood of the lattice site to be updated. In BIO-LGCA, the rule is divided into two steps, a probabilistic interaction step followed by a deterministic transport step. The interaction step simulates reorientation, birth, and death processes, and is defined specifically for the modeled process. The transport step translocates particles to neighboring lattice nodes in the direction of their velocities. See below for details.

State space

For modeling particle velocities explicitly, lattice sites are assumed to have a specific substructure. Each lattice site $\mathbf\in\mathcal$ is connected to its neighboring lattice sites through vectors called "velocity channels", $\mathbf_i$, $i\in\$, where the number of velocity channels $b$ is equal to the number of nearest neighbors, and thus depends on the lattice geometry ($b=2$ for a one-dimensional lattice, $b=6$ for a two-dimensional hexagonal lattice, and so on). In two dimensions, velocity channels are defined as $\mathbf_i=\left(\cos\frac,\sin\frac\right)$. Additionally, an arbitrary number $a$ of so-called "rest channels" may be defined, such that $\mathbf_i=(0,0)$, $i\in\$. A channel is said to be occupied if there is a particle in the lattice site with a velocity equal to the velocity channel. The occupation of channel $\mathbf_i$ is indicated by the occupation number $s_i$. Typically, particles are assumed to obey an exclusion principle, such that no more than one particle may occupy a single velocity channel at a lattice site simultaneously. In this case, occupation numbers are Boolean variables, i.e. $s_i\in\mathcal=\$, and thus, every site has a maximum carrying capacity $K=a+b$. Since the collection of all channel occupation numbers defines the number of particles and their velocities in each lattice site, the vector $\mathbf=\left(s_1,s_2,\ldots,s_\right)$ describes the state of a lattice site, and the state space is given by $\mathcal=\mathcal^K$.

Rule and model dynamics

The states of every site in the lattice are updated synchronously in discrete time steps to simulate the model dynamics. The rule is divided into two steps. The probabilistic interaction step simulates particle interaction, while the deterministic transport step simulates particle movement.

Interaction step

Depending on the specific application, the interaction step may be composed of reaction and/or reorientation operators.

The reaction operator $\mathcal$ replaces the state of a node $\mathbf$ with a new state $\mathbf^$ following a transition probability $P\left(\left. \mathbf\rightarrow \mathbf^\ \mathbf_ \right)$, which depends on the state of the neighboring lattice sites $\mathbf_$ to simulate the influence of neighboring particles on the reactive process. The reaction operator does not conserve particle number, thus allowing to simulate birth and death of individuals. The reaction operator's transition probability is usually defined ''ad hoc'' form phenomenological observations.

The reorientation operator $\mathcal$ also replaces a state $\mathbf$ with a new state $\mathbf^$ with probability $P\left(\left. \mathbf\rightarrow \mathbf^\ \mathbf_ \right)$. However, this operator conserves particle number and therefore only models changes in particle velocity by redistributing particles among velocity channels. The transition probability for this operator can be determined from statistical observations (by using the maximum caliber principle) or from known single-particle dynamics (using the discretized, steady-state angular probability distribution given by the Fokker-Planck equation associated to a Langevin equation describing the reorientation dynamics), and typically takes the form $P\left(\left. \mathbf\rightarrow \mathbf^\ \mathbf_ \right) =\frace^ \delta_$ where $Z$ is a normalization constant (also known as the partition function), $H\left(\mathbf_\right)$ is an energy-like function which particles will likely minimize when changing their direction of motion, $\beta$ is a free parameter inversely proportional to the randomness of particle reorientation (analogous to the inverse temperature in thermodynamics), and $\delta_$ is a Kronecker delta which ensures that particle number before $n\left(\mathbf\right)$ and after reorientation $n\left(\mathbf^\right)$ is unchanged.

The state resulting form applying the reaction and reorientation operator $\mathbf^$ is known as the post-interaction configuration and denoted by $\mathbf^:=\mathbf^$.

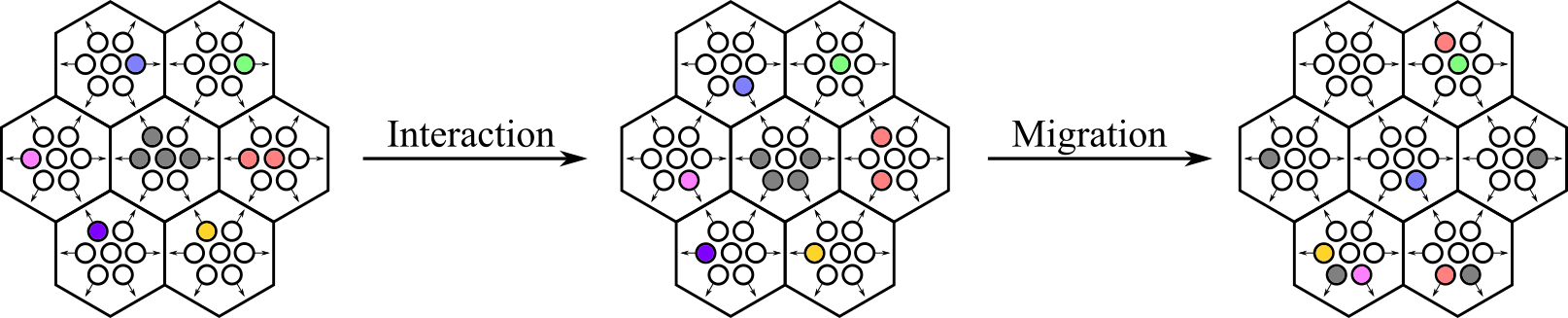
Transport step

After the interaction step, the deterministic transport step is applied synchronously to all lattice sites. The transport step simulates the movement of agents according to their velocity, due to the self-propulsion of living organisms.

During this step, the occupation numbers of post-interaction states will be defined as the new occupation states of the same channel of the neighboring lattice site in the direction of the velocity channel, i.e. $s_i(\mathbf+\mathbf_i)=s_i^(\mathbf)$.

A new time step begins when both interaction and transport steps have occurred. Therefore, the dynamics of the BIO-LGCA can be summarized as the stochastic finite-difference microdynamical equation $s_i(\mathbf+\mathbf_i,k+1)=s_i^(\mathbf,k)$

Example interaction dynamics

The transition probability for the reaction and/or reorientation operator must be defined to appropriately simulate the modeled system. Some elementary interactions and the corresponding transition probabilities are listed below.

Random walk

In the absence of any external or internal stimuli, cells may move randomly without any directional preference. In this case, the reorientation operator may be defined through a transition probability$P\left(\left.\mathbf\rightarrow\mathbf^\\mathbf_\right) =\frac$

where $Z=\sum_\delta_$. Such transition probability allows any post-reorientation configuration $\mathbf^\mathcal$ with the same number of particles as the pre-reorientation configuration $\mathbf$, to be picked uniformly.

Simple birth and death process

If organisms reproduce and die independently of other individuals (with the exception of the finite carrying capacity), then a simple birth/death process can be simulated with a transition probability given byP\left(\left.\mathbf\rightarrow\mathbf^\mathcal\\mathbf_\right)=
\left _b\delta_
+r_d\delta_\right\Theta\left \left(\mathbf^\right)\right\Theta\left \left( K-\mathbf^\right)\right/math> where r_b,r_d\in ,1/math>, $r_b+r_d\leq 1$ are constant birth and death probabilities, respectively, $\delta_$ is the Kronecker delta which ensures only one birth/death event happens every time step, and $\Theta(x)$ is the Heaviside function, which makes sure particle numbers are positive and bounded by the carrying capacity $K$.

Adhesive interactions

Cells may adhere to one another by cadherin molecules on the cell surface. Cadherin interactions allow cells to form aggregates. The formation of cell aggregates via adhesive biomolecules can be modeled by a reorientation operator with transition probabilities defined asP\left(\left.\mathbf\rightarrow\mathbf^\\mathbf_\right)
=\frac\exp\left beta\mathbf\left(\mathbf_\right)\cdot\mathbf\left(\mathbf^\right)\right/math>

where $\mathbf\left(\mathbf_\right)$ is a vector pointing in the direction of maximum cell density, defined as $\mathbf\left(\mathbf_\right)= \sum_\left(\mathbf'-\mathbf\right)n\left(\mathbf_^\right)$, where $\mathbf_^$ is the configuration of the lattice site $\mathbf'$ within the neighborhood $\mathcal$, and $\mathbf\left(\mathbf^\right)$ is the momentum of the post-reorientation configuration, defined as $\mathbf\left(\mathbf^\right)=\sum_^bs_j^\mathbf_j$. This transition probability favors post-reorientation configurations with cells moving towards the cell density gradient.

Mathematical analysis

Since an exact treatment of a stochastic agent-based model quickly becomes unfeasible due to high-order correlations between all agents, the general method of analyzing a BIO-LGCA model is to cast it into an approximate, deterministic finite difference equation (FDE) describing the mean dynamics of the population, then performing the mathematical analysis of this approximate model, and comparing the results to the original BIO-LGCA model.

First, the expected value of the microdynamical equation $s_m(\mathbf+\mathbf_m,k+1)=s_m^(\mathbf,k)$ is obtained$f_m\left(\mathbf+\mathbf_m,k+1\right)= \left\langle s_m^\left(\mathbf,k\right)\right\rangle$ where $\langle\cdot\rangle$ denotes the expected value, and $f_m\left(\mathbf,k\right):=\left\langle s_m\left(\mathbf,k\right)\right\rangle$ is the expected value of the $m$-th channel occupation number of the lattice site at $\mathbf$ at time step $k$. However, the term on the right, $\left\langle s_m^\left(\mathbf,k\right)\right\rangle$ is highly nonlinear on the occupation numbers of both the lattice site $\mathbf$ and the lattice sites within the interaction neighborhood $\mathcal$, due to the form of the transition probability $P\left(\left.\mathbf\rightarrow\mathbf^\\mathbf_\right)$ and the statistics of particle placement within velocity channels (for example, arising from an exclusion principle imposed on channel occupations). This non-linearity would result in high-order correlations and moments among all channel occupations involved. Instead, a mean-field approximation is usually assumed, wherein all correlations and high order moments are neglected, such that direct particle-particle interactions are substituted by interactions with the respective expected values. In other words, if $X_1,X_2,\ldots,X_n$ are random variables, and $F:\mathbb^n\mapsto\mathbb$ is a function, then$\left\langle F\left(X_1,X_2,\ldots,X_n\right)\right\rangle\approx F\left(\left\langle X_1\right\rangle,\left\langle X_2\right\rangle,\ldots,\left\langle X_n\right\rangle\right)$ under this approximation. Thus, we can simplify the equation to$f_m\left(\mathbf+\mathbf_m,k+1\right)= \mathcal\left(\mathbf\left(\mathbf,k\right),\mathbf_\left(\mathbf,k\right)\right)$ where $\mathcal\left(\mathbf\left(\mathbf,k\right),\mathbf_\left(\mathbf,k\right)\right)$ is a nonlinear function of the expected lattice site configuration $\mathbf\left(\mathbf,k\right)$ and the expected neighborhood configuration $\mathbf_\left(\mathbf,k\right)$ dependent on the transition probabilities and in-node particle statistics.

From this nonlinear FDE, one may identify several homogeneous steady states, or constants $\bar_m$ independent of $\mathbf$ and $k$ which are solutions to the FDE. To study the stability conditions of these steady states and the pattern formation potential of the model, a linear stability analysis can be performed. To do so, the nonlinear FDE is linearized as$f_m\left(\mathbf+\mathbf_m,k+1\right)= \sum_^K\left.\frac\_f_j\left(\mathbf,k\right)+ \sum_^K\sum_^K\left.\frac\_f_j\left(\mathbf+\mathbf_p,k\right)$ where $\mathrm$ denotes the homogeneous steady state $f_m\left(\mathbf,k\right)=\bar_m,m\in\$, and a von Neumann neighborhood was assumed. In order to cast it into a more familiar finite difference equation with temporal increments only, a discrete Fourier transform can be applied on both sides of the equation. After applying the shift theorem and isolating the term with a temporal increment on the left, one obtains the lattice-Boltzmann equation$\hat_m\left(\mathbf,k+1\right)=e^ \left\$ where $i=\sqrt$ is the imaginary unit, $L$ is the size of the lattice along one dimension, $\mathbf\in\^d$ is the Fourier wave number, and $\hat=\mathcal\$ denotes the discrete Fourier transform. In matrix notation, this equation is simplified to $\hat\left(\mathbf,k+1\right)=\Gamma\hat\left(\mathbf,k\right)$, where the matrix $\Gamma$ is called the ''Boltzmann propagator'' and is defined as\Gamma_=e^
\left _+\sum_^K\left.\frac\_e^\right The eigenvalues $\lambda\left(\mathbf\right)$ of the Boltzmann propagator dictate the stability properties of the steady state:

* If $\left, \lambda\left(\mathbf\right)\>1$, where $, \cdot,$ denotes the modulus, then perturbations with wave number $\mathbf$ grow with time. If $\left, \lambda\left(\mathbf_\right)\>1$, and $\left, \lambda\left(\mathbf_\right)\\geq\left, \lambda\left(\mathbf\right)\\forall\mathbf\in\^d$, then perturbations with wave number $\mathbf_$ will dominate and patterns with a clear wavelength will be observed. Otherwise, the steady state is stable and any perturbations will decay.
* If \mathrm\left lambda\left(q\right)\rightneq 0, where $\mathrm(\cdot)$ denotes the argument, then perturbations are transported and non-stationary population behaviors are observed. Otherwise, the population will appear static at the macroscopic level.

Applications

Constructing a BIO-LGCA for the study of biological phenomena mainly involves defining appropriate transition probabilities for the interaction operator, though precise definitions of the state space (to consider several cellular phenotypes, for example), boundary conditions (for modeling phenomena in confined conditions), neighborhood (to match experimental interaction ranges quantitatively), and carrying capacity (to simulate crowding effects for given cell sizes) may be important for specific applications. While the distribution of the reorientation operator can be obtained through the aforementioned statistical and biophysical methods, the distribution of the reaction operators can be estimated from the statistics of ''in vitro'' experiments, for example.

BIO-LGCA models have been used to study several cellular, biophysical and medical phenomena. Some examples include:

* Angiogenesis: an in vitro experiment with endothelial cells and BIO-LGCA simulation observables were compared to determine the processes involved during angiogenesis and their weight. They found that adhesion, alignment, contact guidance, and ECM remodeling are all involved in angiogenesis, while long-range interactions are not vital to the process.
* Active fluids: the macroscopic physical properties of a population of particles interacting through polar alignment interactions were investigated using a BIO-LGCA model. It was found that increasing initial particle density and interaction strength result in a second order phase transition from a homogeneous, disordered state to an ordered, patterned, moving state.
* Epidemiology: a spatial SIR BIO-LGCA model was used to study the effect of different vaccination strategies, and the effect of approximating a spatial epidemic with a non-spatial model. They found that barrier-type vaccination strategies are much more effective than spatially uniform vaccination strategies. Furthermore, they found that non-spatial models greatly overestimate the rate of infection.
* Cell jamming: in vitro and Bio-LGCA models were used for studying metastatic behavior in breast cancer. The BIO-LGCA model revealed that metastasis may exhibit different behaviors, such as random gas-like, jammed solid-like, and correlated fluid-like states, depending on the adhesivity level among cells, ECM density, and cell-ECM interactions.

References

{{reflist

External links

Bio-LGCA Simulator
- An online simulator with elementary interactions with personalizable parameter values.

BIO-LGCA Python Package
- An open source Python package for implementing BIO-LGCA model simulations.

Statistical mechanics
Lattice models
Stochastic models
Complex dynamics