|
Zeroth Law Of Thermodynamics
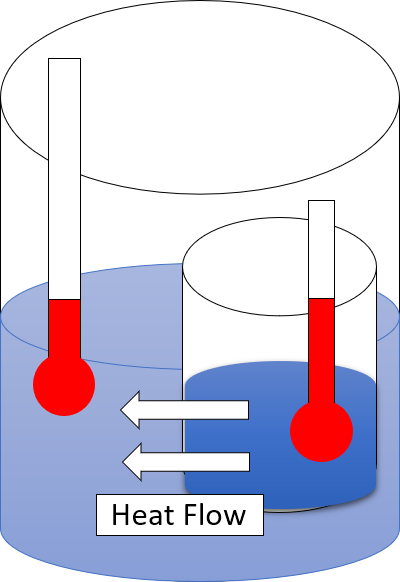
The zeroth law of thermodynamics is one of the four principal laws of thermodynamics. It provides an independent definition of temperature without reference to entropy, which is defined in the second law. The law was established by Ralph H. Fowler in the 1930s, long after the first, second, and third laws had been widely recognized. The zeroth law states that if two thermodynamic systems are both in thermal equilibrium with a third system, then the two systems are in thermal equilibrium with each other.Buchdahl, H.A. (1966). ''The Concepts of Classical Thermodynamics'', Cambridge University Press, Cambridge, p. 29: "... if each of two systems is in equilibrium with a third system then they are in equilibrium with each other." Two systems are said to be in thermal equilibrium if they are linked by a wall permeable only to heat, and they do not change over time. Another formulation by James Clerk Maxwell is "All heat is of the same kind". Another statement of the law is "All dia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laws Of Thermodynamics
The laws of thermodynamics are a set of scientific laws which define a group of physical quantities, such as temperature, energy, and entropy, that characterize thermodynamic systems in thermodynamic equilibrium. The laws also use various parameters for thermodynamic processes, such as thermodynamic work and heat, and establish relationships between them. They state empirical facts that form a basis of precluding the possibility of certain phenomena, such as perpetual motion. In addition to their use in thermodynamics, they are important fundamental laws of physics in general and are applicable in other natural sciences. Traditionally, thermodynamics has recognized three fundamental laws, simply named by an ordinal identification, the first law, the second law, and the third law.Guggenheim, E.A. (1985). ''Thermodynamics. An Advanced Treatment for Chemists and Physicists'', seventh edition, North Holland, Amsterdam, .Kittel, C. Kroemer, H. (1980). ''Thermal Physics'', second ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant under some Transformation (function), transformations, such as Translation (geometry), translation, Reflection (mathematics), reflection, Rotation (mathematics), rotation, or Scaling (geometry), scaling. Although these two meanings of the word can sometimes be told apart, they are intricately related, and hence are discussed together in this article. Mathematical symmetry may be observed with respect to the passage of time; as a space, spatial relationship; through geometric transformations; through other kinds of functional transformations; and as an aspect of abstract objects, including scientific model, theoretic models, language, and music. This article describes symmetry from three perspectives: in mathematics, including geometry, the m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constantin Carathéodory
Constantin Carathéodory (; 13 September 1873 – 2 February 1950) was a Greeks, Greek mathematician who spent most of his professional career in Germany. He made significant contributions to real and complex analysis, the calculus of variations, and measure theory. He also created an axiomatic formulation of thermodynamics. Carathéodory is considered one of the greatest mathematicians of his era and the most renowned Greek mathematics, Greek mathematician since Ancient history, antiquity. Origins Constantin Carathéodory was born in 1873 in Berlin to Greeks, Greek parents and grew up in Brussels. His father , a lawyer, served as the Ottoman Empire, Ottoman ambassador to Belgium, St. Petersburg and Berlin. His mother, Despina, née Petrokokkinos, was from the island of Chios. The Carathéodory family, originally from Bosna, Edirne, Bosna, was well established and respected in Istanbul, Constantinople, and its members held many important governmental positions. His grandfather ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arnold Sommerfeld
Arnold Johannes Wilhelm Sommerfeld (; 5 December 1868 – 26 April 1951) was a German Theoretical physics, theoretical physicist who pioneered developments in Atomic physics, atomic and Quantum mechanics, quantum physics, and also educated and mentored many students for the new era of theoretical physics. He served as doctoral advisor and Postdoctoral researcher, postdoc advisor to seven Nobel Prize winners and supervised at least 30 other famous physicists and chemists. Only J. J. Thomson's record of mentorship offers a comparable list of high-achieving students. He introduced the second quantum number, azimuthal quantum number, and the third quantum number, magnetic quantum number. He also introduced the fine-structure constant and pioneered X-ray wave theory. Early life and education Sommerfeld was born in 1868 to a family with deep ancestral roots in Prussia. His mother Cäcilie Matthias (1839–1902) was the daughter of a Potsdam builder. His father Franz Sommerfeld (1820� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mole (unit)
The mole (symbol mol) is a unit of measurement, the base unit in the International System of Units (SI) for ''amount of substance'', an SI base quantity proportional to the number of elementary entities of a substance. One mole is an aggregate of exactly elementary entities (approximately 602 sextillion or 602 billion times a trillion), which can be atoms, molecules, ions, ion pairs, or other particles. The number of particles in a mole is the Avogadro number (symbol ) and the numerical value of the '' Avogadro constant'' (symbol ) expressed in mol−1. The relationship between the mole, Avogadro number, and Avogadro constant can be expressed in the following equation:1\text = \frac = \frac The current SI value of the mole is based on the historical definition of the mole as the amount of substance that corresponds to the number of atoms in 12 grams of 12C, which made the molar mass of a compound in grams per mole, numerically equal to the average molecular mass or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordinate is needed to specify a point on itfor example, the point at 5 on a number line. A surface, such as the boundary of a cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on itfor example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces. In classical mechanics, space and time are different categories and refer to absolute space and time. That conception of the world is a four-dimensional space but not the one that w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Temperature
Thermodynamic temperature, also known as absolute temperature, is a physical quantity which measures temperature starting from absolute zero, the point at which particles have minimal thermal motion. Thermodynamic temperature is typically expressed using the Kelvin scale, where the unit of measurement is the ''kelvin'' (unit symbol: K). The Kelvin scale uses the same degree interval as the Celsius scale but is offset so that 0 K corresponds to absolute zero. For comparison, a temperature of 295 K corresponds to 21.85 °C and 71.33 °F. Another absolute scale of temperature is the Rankine scale, which is based on the Fahrenheit degree interval. Historically, thermodynamic temperature was defined by Lord Kelvin in terms of a macroscopic relation between Work (thermodynamics), thermodynamic work and Heat, heat transfer as defined in thermodynamics, but the kelvin was redefined by international agreement in 2019 in terms of phenomena that are now understood as man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second Law Of Thermodynamics
The second law of thermodynamics is a physical law based on Universal (metaphysics), universal empirical observation concerning heat and Energy transformation, energy interconversions. A simple statement of the law is that heat always flows spontaneously from hotter to colder regions of matter (or 'downhill' in terms of the temperature gradient). Another statement is: "Not all heat can be converted into Work (thermodynamics), work in a cyclic process."Young, H. D; Freedman, R. A. (2004). ''University Physics'', 11th edition. Pearson. p. 764. The second law of thermodynamics establishes the concept of entropy as a physical property of a thermodynamic system. It predicts whether processes are forbidden despite obeying the requirement of conservation of energy as expressed in the first law of thermodynamics and provides necessary criteria for spontaneous processes. For example, the first law allows the process of a cup falling off a table and breaking on the floor, as well as allowi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scale Of Temperature
Scale of temperature is a methodology of calibrating the physical quantity temperature in metrology. Empirical scales measure temperature in relation to convenient and stable parameters or reference points, such as the freezing and boiling point of water. Absolute temperature is based on thermodynamic principles: using the lowest possible temperature as the zero point, and selecting a convenient incremental unit. Celsius, Kelvin, and Fahrenheit are common temperature scales. Other scales used throughout history include Rankine, Rømer, Newton, Delisle, Réaumur, Gas mark, Leiden, and Wedgwood. Technical definition The zeroth law of thermodynamics describes thermal equilibrium between thermodynamic systems in form of an equivalence relation. Accordingly, the set of all thermal systems may be divided into a quotient set of equivalence classes, denoted as M, where any element of M collects all systems that are in thermal equilibrium with one another. If the set M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermometer
A thermometer is a device that measures temperature (the hotness or coldness of an object) or temperature gradient (the rates of change of temperature in space). A thermometer has two important elements: (1) a temperature sensor (e.g. the bulb of a mercury-in-glass thermometer or the pyrometric sensor in an infrared thermometer) in which some change occurs with a change in temperature; and (2) some means of converting this change into a numerical value (e.g. the visible scale that is marked on a mercury-in-glass thermometer or the digital readout on an infrared model). Thermometers are widely used in technology and industry to monitor processes, in meteorology, in medicine (''medical thermometer''), and in scientific research. A standard scale While an individual thermometer is able to measure degrees of hotness, the readings on two thermometers cannot be compared unless they conform to an agreed scale. Today there is an absolute thermodynamic temperature scale. Internat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number System
In mathematics, a real number is a number that can be used to measure a continuous one-dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers, sometimes called "the reals", is traditionally denoted by a bold , often using blackboard bold, . The adjective ''real'', used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of . The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers are called irrational numbers. Some irrational numbers (as well as all the rationals) are the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |