|
Trace Diagram
In mathematics, trace diagrams are a graphical means of performing computations in linear algebra, linear and multilinear algebra. They can be represented as (slightly modified) graph theory, graphs in which some edges are labeled by matrix (mathematics), matrices. The simplest trace diagrams represent the trace (linear algebra), trace and determinant of a matrix. Several results in linear algebra, such as Cramer's Rule and the Cayley–Hamilton theorem, have simple diagrammatic proofs. They are closely related to Penrose's graphical notation. Formal definition Let ''V'' be a vector space of vector space, dimension ''n'' over a field (mathematics), field ''F'' (with ''n''≥2), and let Hom(''V'',''V'') denote the linear transformations on ''V''. An ''n''-trace diagram is a Graph (discrete mathematics), graph \mathcal=(V_1\sqcup V_2\sqcup V_n, E), where the sets ''V''''i'' (''i'' = 1, 2, ''n'') are composed of Vertex (graph theory), vertices of Degree (graph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trace Diagram Adjugate
Trace may refer to: Arts and entertainment Music * Trace (Son Volt album), ''Trace'' (Son Volt album), 1995 * Trace (Died Pretty album), ''Trace'' (Died Pretty album), 1993 * Trace (band), a Dutch progressive rock band * The Trace (album), ''The Trace'' (album) Other uses in arts and entertainment * Trace (magazine), ''Trace'' (magazine), British hip-hop magazine * Trace (manhwa), ''Trace'' (manhwa), a Korean internet cartoon * Trace (novel), ''Trace'' (novel), a novel by Patricia Cornwell * The Trace (film), ''The Trace'' (film), a 1994 Turkish film * The Trace (video game), ''The Trace'' (video game), 2015 video game * Sama (film), ''Sama'' (film), alternate title ''The Trace'', a 1988 Tunisian film * Trace, a fictional character in the game ''Metroid Prime Hunters'' * Trace, the protagonist of ''Axiom Verge'' * Trace, another name for List of One Piece characters#Portgas D. Ace, Portgas D. Ace, a fictional character in the manga ''One Piece'' * TRACE, the main brand for a numb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Loop (graph Theory)
In graph theory, a loop (also called a self-loop or a ''buckle'') is an edge that connects a vertex to itself. A simple graph contains no loops. Depending on the context, a graph or a multigraph may be defined so as to either allow or disallow the presence of loops (often in concert with allowing or disallowing multiple edges between the same vertices): * Where graphs are defined so as to ''allow'' loops and multiple edges, a graph without loops or multiple edges is often distinguished from other graphs by calling it a ''simple graph''. * Where graphs are defined so as to ''disallow'' loops and multiple edges, a graph that does have loops or multiple edges is often distinguished from the graphs that satisfy these constraints by calling it a ''multigraph'' or '' pseudograph''. In a graph with one vertex, all edges must be loops. Such a graph is called a bouquet. Degree For an undirected graph, the degree of a vertex is equal to the number of adjacent vertices. A special case ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trace Diagram Quadruple Product Identity
Trace may refer to: Arts and entertainment Music * ''Trace'' (Son Volt album), 1995 * ''Trace'' (Died Pretty album), 1993 * Trace (band), a Dutch progressive rock band * ''The Trace'' (album) Other uses in arts and entertainment * ''Trace'' (magazine), British hip-hop magazine * ''Trace'' (manhwa), a Korean internet cartoon * ''Trace'' (novel), a novel by Patricia Cornwell * ''The Trace'' (film), a 1994 Turkish film * ''The Trace'' (video game), 2015 video game * ''Sama'' (film), alternate title ''The Trace'', a 1988 Tunisian film * Trace, a fictional character in the game ''Metroid Prime Hunters'' * Trace, the protagonist of ''Axiom Verge'' * Trace, another name for Portgas D. Ace, a fictional character in the manga ''One Piece'' * TRACE, the main brand for a number of music channels such as Trace Urban Language * Trace (deconstruction), a concept in Derridian deconstruction * Trace (linguistics), a syntactic placeholder resulting from a transformation * TRACE (psychol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dot Product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors), and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called the inner product (or rarely projection product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space (see Inner product space for more). Algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. These definitions are equivalent when using Cartesian coordinates. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross Product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and is denoted by the symbol \times. Given two linearly independent vectors and , the cross product, (read "a cross b"), is a vector that is perpendicular to both and , and thus normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with the dot product (projection product). If two vectors have the same direction or have the exact opposite direction from each other (that is, they are ''not'' linearly independent), or if either one has zero length, then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular, the magnitude of the product of two per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Identities
The following are important identities involving derivatives and integrals in vector calculus. Operator notation Gradient For a function f(x, y, z) in three-dimensional Cartesian coordinate variables, the gradient is the vector field: \operatorname(f) = \nabla f = \begin \frac,\ \frac,\ \frac \end f = \frac \mathbf + \frac \mathbf + \frac \mathbf where i, j, k are the standard unit vectors for the ''x'', ''y'', ''z''-axes. More generally, for a function of ''n'' variables \psi(x_1, \ldots, x_n), also called a scalar field, the gradient is the vector field: \nabla\psi = \begin\frac, \ldots,\ \frac \end\psi = \frac \mathbf_1 + \dots + \frac\mathbf_n . where \mathbf_ are orthogonal unit vectors in arbitrary directions. As the name implies, the gradient is proportional to and points in the direction of the function's most rapid (positive) change. For a vector field \mathbf = \left(A_1, \ldots, A_n\right) written as a 1 × ''n'' row vector, also called a te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edge Coloring
In graph theory, an edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most different colors, for a given value of , or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three. By Vizing's theorem, the number of colors needed to edge color a simple graph is either its maximum degree or . For some graphs, such as bipartite graphs and high-degree planar graphs, the number of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
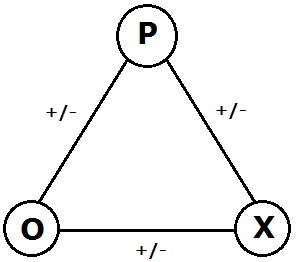
Signed Graph
In the area of graph theory in mathematics, a signed graph is a graph in which each edge has a positive or negative sign. A signed graph is balanced if the product of edge signs around every cycle is positive. The name "signed graph" and the notion of balance appeared first in a mathematical paper of Frank Harary in 1953. Dénes Kőnig had already studied equivalent notions in 1936 under a different terminology but without recognizing the relevance of the sign group. At the Center for Group Dynamics at the University of Michigan, Dorwin Cartwright and Harary generalized Fritz Heider's psychological theory of balance in triangles of sentiments to a psychological theory of balance in signed graphs. Signed graphs have been rediscovered many times because they come up naturally in many unrelated areas. For instance, they enable one to describe and analyze the geometry of subsets of the classical root systems. They appear in topological graph theory and group theory. They are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anti-symmetric Tensor
In mathematics and theoretical physics, a tensor is antisymmetric on (or with respect to) an index subset if it alternates sign (+/−) when any two indices of the subset are interchanged. section §7. The index subset must generally either be all ''covariant'' or all ''contravariant''. For example, T_ = -T_ = T_ = -T_ = T_ = -T_ holds when the tensor is antisymmetric with respect to its first three indices. If a tensor changes sign under exchange of ''each'' pair of its indices, then the tensor is completely (or totally) antisymmetric. A completely antisymmetric covariant tensor field of order k may be referred to as a differential k-form, and a completely antisymmetric contravariant tensor field may be referred to as a k-vector field. Antisymmetric and symmetric tensors A tensor A that is antisymmetric on indices i and j has the property that the contraction with a tensor B that is symmetric on indices i and j is identically 0. For a general tensor U with components U_ and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |