|
Tetrahemihexahedron
In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 7 faces (4 triangles and 3 squares), 12 edges, and 6 vertices. Its vertex figure is a crossed quadrilateral. Its Coxeter–Dynkin diagram is (although this is a double covering of the tetrahemihexahedron). The tetrahemihexahedron is the only non-prismatic uniform polyhedron with an odd number of faces. Its Wythoff symbol is 3/2 3 , 2, but that represents a double covering of the tetrahemihexahedron with eight triangles and six squares, paired and coinciding in space. (It can more intuitively be seen as two coinciding tetrahemihexahedra.) The tetrahemihexahedron is a hemipolyhedron. The "hemi" part of the name means some of the faces form a group with half as many members as some regular polyhedron—here, three square faces form a group with half as many faces as the regular hexahedron, better known as the cube—hence ''hemihexahedron''. Hemi faces are also oriented ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e., an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is Cuboctahedron#Radial equilateral symmetry, radially equilateral. Its dual polyhedron is the rhombic dodecahedron. Construction The cuboctahedron can be constructed in many ways: * Its construction can be started by attaching two regular triangular cupolas base-to-base. This is similar to one of the Johnson solids, triangular orthobicupola. The difference is that the triangular orthobicupola is constructed with one of the cupolas twisted so that similar polygonal faces are adjacent, whereas the cuboctahedron is not. As a result, the cuboctahedron may also called the ''triangular gyro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonconvex Uniform Polyhedron
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, or both. The complete set of 57 nonprismatic uniform star polyhedra includes the 4 regular ones, called the Kepler–Poinsot polyhedron, Kepler–Poinsot polyhedra, 14 Quasiregular polyhedron#Nonconvex examples, quasiregular ones, and 39 semiregular ones. There are also two infinite sets of Uniform_polyhedron#.28p_2_2.29_Prismatic_.5Bp.2C2.5D.2C_I2.28p.29_family_.28Dph_dihedral_symmetry.29, ''uniform star prisms'' and ''uniform star antiprisms''. Just as (nondegenerate) star polygons (which have density (polytope), polygon density greater than 1) correspond to circular polygons with overlapping Tessellation, tiles, star polyhedra that do not pass through the center have polytope density greater than 1, and correspond to spherical polyhe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
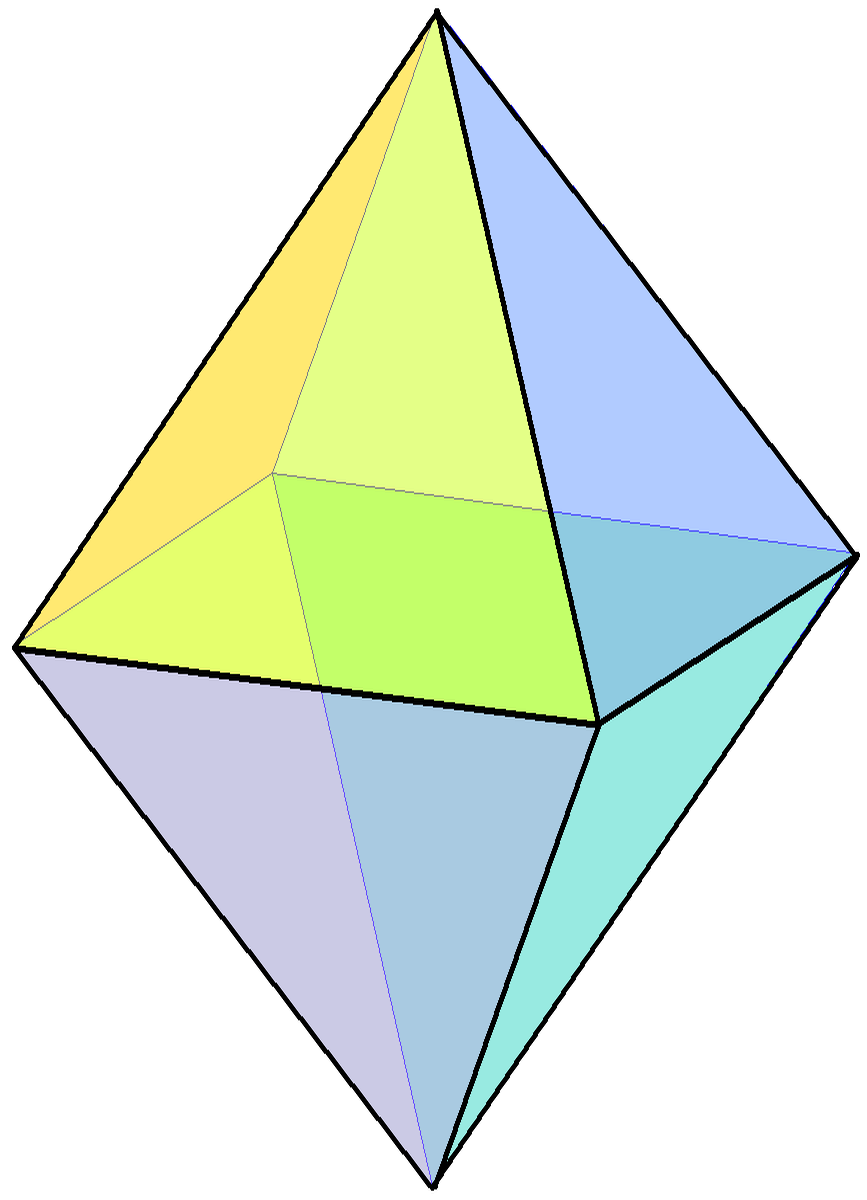
Regular Octahedron
In geometry, a regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. An octahedron, more generally, can be any eight-sided polyhedron; many types of irregular octahedra also exist. A regular octahedron is convex, meaning that for any two points within it, the line segment connecting them lies entirely within it. It is one of the eight convex deltahedra because all of the faces are equilateral triangles. It is a composite polyhedron made by attaching two equilateral square pyramids. Its dual polyhedron is the cube, and they have the same three-dimensional symmetry groups, the octahedral symmetry \mathrm_\mathrm . A regular octahedron is a special case of an octahedron, any eight-sided polyhedron. It is the three-dimensional case of the more general concept of a cross-polytope. As a Platonic solid The regular octahedron is one of the Platonic solids, a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonconvex Uniform Polyhedron
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, or both. The complete set of 57 nonprismatic uniform star polyhedra includes the 4 regular ones, called the Kepler–Poinsot polyhedron, Kepler–Poinsot polyhedra, 14 Quasiregular polyhedron#Nonconvex examples, quasiregular ones, and 39 semiregular ones. There are also two infinite sets of Uniform_polyhedron#.28p_2_2.29_Prismatic_.5Bp.2C2.5D.2C_I2.28p.29_family_.28Dph_dihedral_symmetry.29, ''uniform star prisms'' and ''uniform star antiprisms''. Just as (nondegenerate) star polygons (which have density (polytope), polygon density greater than 1) correspond to circular polygons with overlapping Tessellation, tiles, star polyhedra that do not pass through the center have polytope density greater than 1, and correspond to spherical polyhe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiparallelogram
In geometry, an antiparallelogram is a type of list of self-intersecting polygons, self-crossing quadrilateral. Like a parallelogram, an antiparallelogram has two opposite pairs of equal-length sides, but these pairs of sides are not in general parallel (geometry), parallel. Instead, each pair of sides is antiparallel lines, antiparallel with respect to the other, with sides in the longer pair crossing each other as in a scissors mechanism. Whereas a parallelogram's opposite angles are equal and oriented the same way, an antiparallelogram's are equal but oppositely oriented. Antiparallelograms are also called contraparallelograms or crossed parallelograms. Antiparallelograms occur as the vertex figures of certain nonconvex uniform polyhedron, nonconvex uniform polyhedra. In the theory of four-bar linkages, the linkages with the form of an antiparallelogram are also called butterfly linkages or bow-tie linkages, and are used in the design of non-circular gears. In celestial mechan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Star Polyhedron
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, or both. The complete set of 57 nonprismatic uniform star polyhedra includes the 4 regular ones, called the Kepler–Poinsot polyhedra, 14 quasiregular ones, and 39 semiregular ones. There are also two infinite sets of ''uniform star prisms'' and ''uniform star antiprisms''. Just as (nondegenerate) star polygons (which have polygon density greater than 1) correspond to circular polygons with overlapping tiles, star polyhedra that do not pass through the center have polytope density greater than 1, and correspond to spherical polyhedra with overlapping tiles; there are 47 nonprismatic such uniform star polyhedra. The remaining 10 nonprismatic uniform star polyhedra, those that pass through the center, are the hemipolyhedra as well as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hemi-cuboctahedron
A hemi-cuboctahedron is an abstract polyhedron, containing half the faces of a semiregular cuboctahedron. It has 4 triangular faces and 3 square faces, 12 edges, and 6 vertices. It can be seen as a rectified hemi-octahedron or rectified hemi-cube. Its skeleton matches 6 vertices and 12 edges of a regular octahedron. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 4 triangles and 3 square), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected. Dual Its dual polyhedron is a rhombic hemi-dodecahedron which has 7 vertices (1-7), 12 edges (a-l), and 6 rhombic faces (A-F). : Related polyhedra It has a real presentation as a uniform star polyhedron, the tetrahemihexahedron. : See also *Hemi-dodecahedron *Hemi-icosahedron In geometry, a hemi-icosahedron is an abstract polytope, abstract regular polyhedron, containing half the faces of a regular icosahed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abstract Polyhedron
In mathematics, an abstract polytope is an algebraic partially ordered set which captures the dyadic property of a traditional polytope without specifying purely geometric properties such as points and lines. A geometric polytope is said to be a ''realization'' of an abstract polytope in some real N-dimensional space, typically Euclidean. This abstract definition allows more general combinatorial structures than traditional definitions of a polytope, thus allowing new objects that have no counterpart in traditional theory. Introductory concepts Traditional versus abstract polytopes In Euclidean geometry, two shapes that are not similar can nonetheless share a common structure. For example, a square and a trapezoid both comprise an alternating chain of four vertices and four sides, which makes them quadrilaterals. They are said to be isomorphic or “structure preserving”. This common structure may be represented in an underlying abstract polytope, a purely algebra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covering Space
In topology, a covering or covering projection is a continuous function, map between topological spaces that, intuitively, Local property, locally acts like a Projection (mathematics), projection of multiple copies of a space onto itself. In particular, coverings are special types of local homeomorphisms. If p : \tilde X \to X is a covering, (\tilde X, p) is said to be a covering space or cover of X, and X is said to be the base of the covering, or simply the base. By abuse of terminology, \tilde X and p may sometimes be called covering spaces as well. Since coverings are local homeomorphisms, a covering space is a special kind of étalé space. Covering spaces first arose in the context of complex analysis (specifically, the technique of analytic continuation), where they were introduced by Bernhard Riemann, Riemann as domains on which naturally multivalued function, multivalued complex functions become single-valued. These spaces are now called Riemann surfaces. Covering spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedral Symmetry
image:tetrahedron.svg, 150px, A regular tetrahedron, an example of a solid with full tetrahedral symmetry A regular tetrahedron has 12 rotational (or orientation-preserving) symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation. The group of all (not necessarily orientation preserving) symmetries is isomorphic to the group S4, the symmetric group of permutations of four objects, since there is exactly one such symmetry for each permutation of the vertices of the tetrahedron. The set of orientation-preserving symmetries forms a group referred to as the alternating group, alternating subgroup A4 of S4. Details Chiral and full (or achiral tetrahedral symmetry and pyritohedral symmetry) are Point groups in three dimensions, discrete point symmetries (or equivalently, List of spherical symmetry groups, symmetries on the sphere). They are among the Crystal system#Overview of point groups by crystal system, crystallographic point gro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent. It is commonly denoted by \chi (Greek alphabet, Greek lower-case letter chi (letter), chi). The Euler characteristic was originally defined for polyhedron, polyhedra and used to prove various theorems about them, including the classification of the Platonic solids. It was stated for Platonic solids in 1537 in an unpublished manuscript by Francesco Maurolico. Leonhard Euler, for whom the concept is named, introduced it for convex polyhedra more generally but failed to rigorously prove that it is an invariant. In modern mathematics, the Euler characteristic arises from homology (mathematics), homology and, more abstractly, homological algebra. Polyhedra The Euler characteristic was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |