|
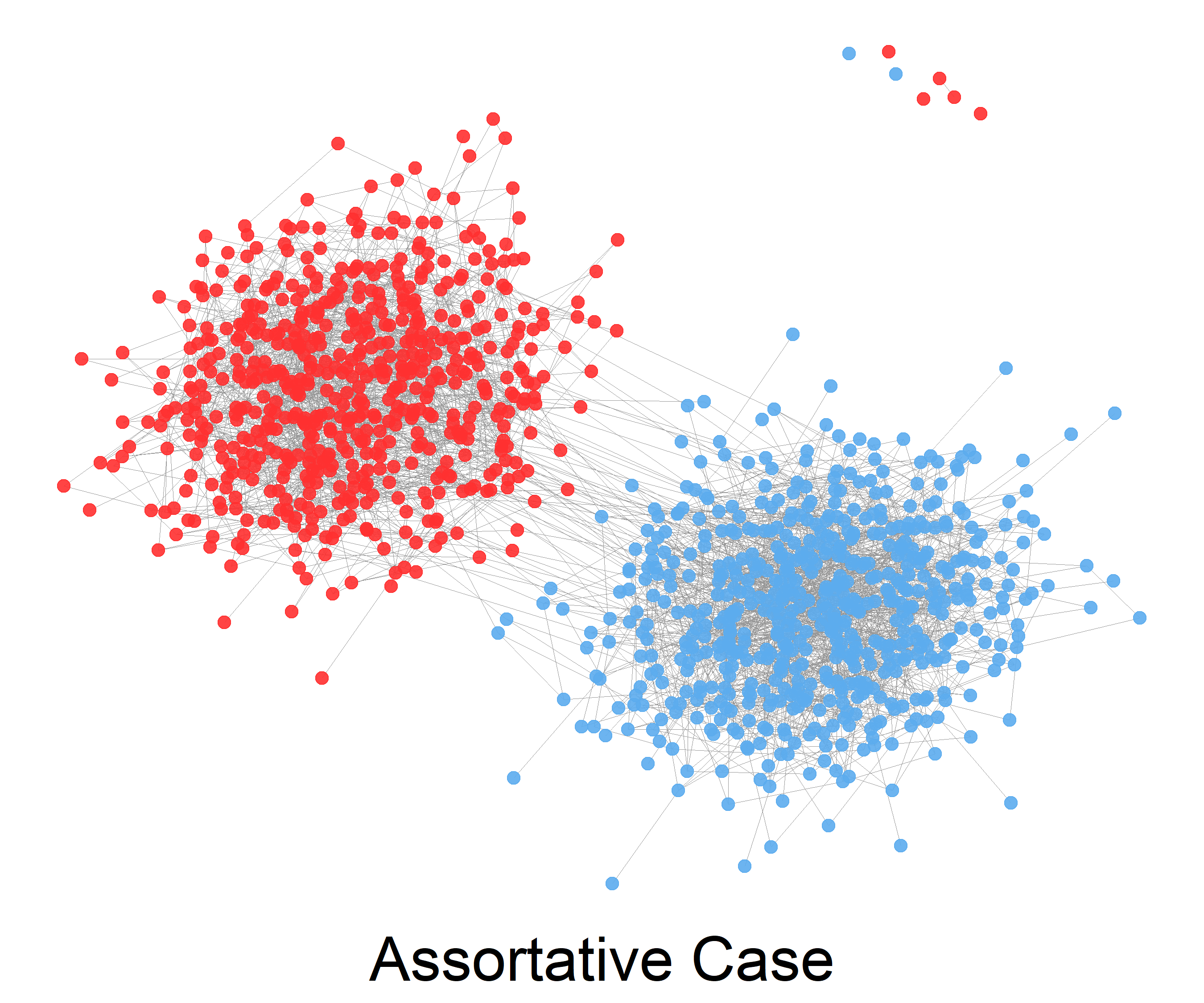
Stochastic Block Model
The stochastic block model is a generative model for random graphs. This model tends to produce graphs containing ''communities'', subsets of nodes characterized by being connected with one another with particular edge densities. For example, edges may be more common within communities than between communities. Its mathematical formulation was first introduced in 1983 in the field of social network analysis by Paul W. Holland et al. The stochastic block model is important in statistics, machine learning, and network science, where it serves as a useful benchmark for the task of recovering community structure in graph data. Definition The stochastic block model takes the following parameters: * The number n of vertices; * a partition of the vertex set \ into disjoint subsets C_1,\ldots,C_r, called ''communities''; * a symmetric r \times r matrix P of edge probabilities. The edge set is then sampled at random as follows: any two vertices u \in C_i and v \in C_j are connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regularization (mathematics)
In mathematics, statistics, Mathematical finance, finance, and computer science, particularly in machine learning and inverse problems, regularization is a process that converts the Problem solving, answer to a problem to a simpler one. It is often used in solving ill-posed problems or to prevent overfitting. Although regularization procedures can be divided in many ways, the following delineation is particularly helpful: * Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be Prior probability, priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique. * Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularizat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Graphs
In mathematics, random graph is the general term to refer to probability distributions over Graph (discrete mathematics), graphs. Random graphs may be described simply by a probability distribution, or by a random process which generates them. The theory of random graphs lies at the intersection between graph theory and probability theory. From a mathematical perspective, random graphs are used to answer questions about the properties of ''typical'' graphs. Its practical applications are found in all areas in which complex networks need to be modeled – many random graph models are thus known, mirroring the diverse types of complex networks encountered in different areas. In a mathematical context, ''random graph'' refers almost exclusively to the Erdős–Rényi model, Erdős–Rényi random graph model. In other contexts, any graph model may be referred to as a ''random graph''. Models A random graph is obtained by starting with a set of ''n'' isolated vertices and add ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Networks
A social network is a social structure consisting of a set of social actors (such as individuals or organizations), networks of dyadic ties, and other social interactions between actors. The social network perspective provides a set of methods for analyzing the structure of whole social entities along with a variety of theories explaining the patterns observed in these structures. The study of these structures uses social network analysis to identify local and global patterns, locate influential entities, and examine dynamics of networks. For instance, social network analysis has been used in studying the spread of misinformation on social media platforms or analyzing the influence of key figures in social networks. Social networks and the analysis of them is an inherently interdisciplinary academic field which emerged from social psychology, sociology, statistics, and graph theory. Georg Simmel authored early structural theories in sociology emphasizing the dynamics of tria ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blockmodeling
Blockmodeling is a set or a coherent Conceptual framework, framework, that is used for analyzing social structure and also for setting procedure(s) for partitioning (clustering) social network's units (Node (computer science), nodes, vertices, social actor, actors), based on specific patterns, which form a distinctive structure through interconnectivity.Patrick Doreian, An Intuitive Introduction to Blockmodeling with Examples, ''BMS: Bulletin of Sociological Methodology'' / ''Bulletin de Méthodologie Sociologique'', January, 1999, No. 61 (January, 1999), pp. 5–34. It is primarily used in statistics, machine learning and network science. As an empirical procedure, blockmodeling assumes that all the units in a specific network can be grouped together to such extent to which they are equivalent. Regarding equivalency, it can be structural, regular or generalized.Anuška Ferligoj: Blockmodeling, http://mrvar.fdv.uni-lj.si/sola/info4/nusa/doc/blockmodeling-2.pdf Using blockmodeling, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Clustering
In multivariate statistics, spectral clustering techniques make use of the spectrum (eigenvalues) of the similarity matrix of the data to perform dimensionality reduction before clustering in fewer dimensions. The similarity matrix is provided as an input and consists of a quantitative assessment of the relative similarity of each pair of points in the dataset. In application to image segmentation, spectral clustering is known as segmentation-based object categorization. Definitions Given an enumerated set of data points, the similarity matrix may be defined as a symmetric matrix A, where A_\geq 0 represents a measure of the similarity between data points with indices i and j. The general approach to spectral clustering is to use a standard clustering method (there are many such methods, ''k''-means is discussed below) on relevant eigenvectors of a Laplacian matrix of A. There are many different ways to define a Laplacian which have different mathematical interpretatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topic Model
In statistics and natural language processing, a topic model is a type of statistical model for discovering the abstract "topics" that occur in a collection of documents. Topic modeling is a frequently used text-mining tool for discovery of hidden semantic structures in a text body. Intuitively, given that a document is about a particular topic, one would expect particular words to appear in the document more or less frequently: "dog" and "bone" will appear more often in documents about dogs, "cat" and "meow" will appear in documents about cats, and "the" and "is" will appear approximately equally in both. A document typically concerns multiple topics in different proportions; thus, in a document that is 10% about cats and 90% about dogs, there would probably be about 9 times more dog words than cat words. The "topics" produced by topic modeling techniques are clusters of similar words. A topic model captures this intuition in a mathematical framework, which allows examining a set o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Categorical Distribution
In probability theory and statistics, a categorical distribution (also called a generalized Bernoulli distribution, multinoulli distribution) is a discrete probability distribution that describes the possible results of a random variable that can take on one of ''K'' possible categories, with the probability of each category separately specified. There is no innate underlying ordering of these outcomes, but numerical labels are often attached for convenience in describing the distribution, (e.g. 1 to ''K''). The ''K''-dimensional categorical distribution is the most general distribution over a ''K''-way event; any other discrete distribution over a size-''K'' sample space is a special case. The parameters specifying the probabilities of each possible outcome are constrained only by the fact that each must be in the range 0 to 1, and all must sum to 1. The categorical distribution is the generalization of the Bernoulli distribution for a categorical random variable, i.e. for a dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Belief Propagation
Belief propagation, also known as sum–product message passing, is a message-passing algorithm for performing inference on graphical models, such as Bayesian networks and Markov random fields. It calculates the marginal distribution for each unobserved node (or variable), conditional on any observed nodes (or variables). Belief propagation is commonly used in artificial intelligence and information theory, and has demonstrated empirical success in numerous applications, including low-density parity-check codes, turbo codes, free energy approximation, and satisfiability. The algorithm was first proposed by Judea Pearl in 1982, who formulated it as an exact inference algorithm on trees, later extended to polytrees. While the algorithm is not exact on general graphs, it has been shown to be a useful approximate algorithm. Motivation Given a finite set of discrete random variables X_1, \ldots, X_n with joint probability mass function p, a common task is to compute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semidefinite Programming
Semidefinite programming (SDP) is a subfield of mathematical programming concerned with the optimization of a linear objective function (a user-specified function that the user wants to minimize or maximize) over the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron. Semidefinite programming is a relatively new field of optimization which is of growing interest for several reasons. Many practical problems in operations research and combinatorial optimization can be modeled or approximated as semidefinite programming problems. In automatic control theory, SDPs are used in the context of linear matrix inequalities. SDPs are in fact a special case of cone programming and can be efficiently solved by interior point methods. All linear programs and (convex) quadratic programs can be expressed as SDPs, and via hierarchies of SDPs the solutions of polynomial optimization problems can be approximated. Semidefinite programming ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Clustering
In multivariate statistics, spectral clustering techniques make use of the spectrum (eigenvalues) of the similarity matrix of the data to perform dimensionality reduction before clustering in fewer dimensions. The similarity matrix is provided as an input and consists of a quantitative assessment of the relative similarity of each pair of points in the dataset. In application to image segmentation, spectral clustering is known as segmentation-based object categorization. Definitions Given an enumerated set of data points, the similarity matrix may be defined as a symmetric matrix A, where A_\geq 0 represents a measure of the similarity between data points with indices i and j. The general approach to spectral clustering is to use a standard clustering method (there are many such methods, ''k''-means is discussed below) on relevant eigenvectors of a Laplacian matrix of A. There are many different ways to define a Laplacian which have different mathematical interpretatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NP-complete
In computational complexity theory, NP-complete problems are the hardest of the problems to which ''solutions'' can be verified ''quickly''. Somewhat more precisely, a problem is NP-complete when: # It is a decision problem, meaning that for any input to the problem, the output is either "yes" or "no". # When the answer is "yes", this can be demonstrated through the existence of a short (polynomial length) ''solution''. # The correctness of each solution can be verified quickly (namely, in polynomial time) and a brute-force search algorithm can find a solution by trying all possible solutions. # The problem can be used to simulate every other problem for which we can verify quickly that a solution is correct. Hence, if we could find solutions of some NP-complete problem quickly, we could quickly find the solutions of every other problem to which a given solution can be easily verified. The name "NP-complete" is short for "nondeterministic polynomial-time complete". In this name, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |