Regularization (mathematics) on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 Enforcing a sparsity constraint on can lead to simpler and more interpretable models. This is useful in many real-life applications such as
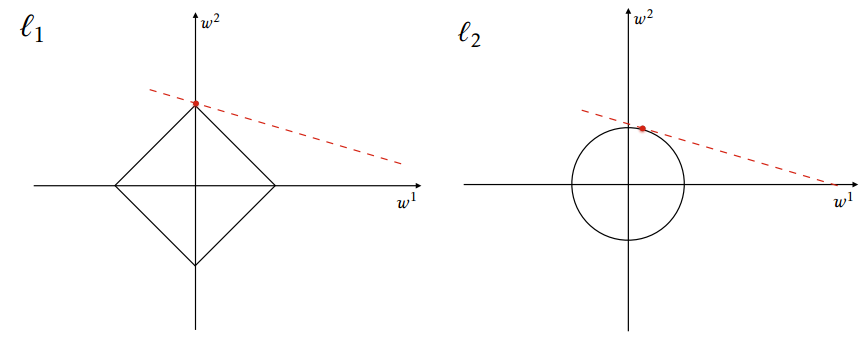
Enforcing a sparsity constraint on can lead to simpler and more interpretable models. This is useful in many real-life applications such as  regularization can occasionally produce non-unique solutions. A simple example is provided in the figure when the space of possible solutions lies on a 45 degree line. This can be problematic for certain applications, and is overcome by combining with regularization in elastic net regularization, which takes the following form:
regularization can occasionally produce non-unique solutions. A simple example is provided in the figure when the space of possible solutions lies on a 45 degree line. This can be problematic for certain applications, and is overcome by combining with regularization in elastic net regularization, which takes the following form:
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
, finance
Finance refers to monetary resources and to the study and Academic discipline, discipline of money, currency, assets and Liability (financial accounting), liabilities. As a subject of study, is a field of Business administration, Business Admin ...
, and computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
, particularly in machine learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task ( ...
and inverse problem
An inverse problem in science is the process of calculating from a set of observations the causal factors that produced them: for example, calculating an image in X-ray computed tomography, sound source reconstruction, source reconstruction in ac ...
s, regularization is a process that converts the answer to a problem to a simpler one. It is often used in solving ill-posed problems or to prevent overfitting
In mathematical modeling, overfitting is "the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit to additional data or predict future observations reliably". An overfi ...
.
Although regularization procedures can be divided in many ways, the following delineation is particularly helpful:
* Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique.
* Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularization is essentially ubiquitous in modern machine learning approaches, including stochastic gradient descent
Stochastic gradient descent (often abbreviated SGD) is an Iterative method, iterative method for optimizing an objective function with suitable smoothness properties (e.g. Differentiable function, differentiable or Subderivative, subdifferentiable ...
for training deep neural networks
Deep learning is a subset of machine learning that focuses on utilizing multilayered neural networks to perform tasks such as classification, regression, and representation learning. The field takes inspiration from biological neuroscience a ...
, and ensemble methods (such as random forest
Random forests or random decision forests is an ensemble learning method for statistical classification, classification, regression analysis, regression and other tasks that works by creating a multitude of decision tree learning, decision trees ...
s and gradient boosted trees
Gradient boosting is a machine learning technique based on Boosting (machine learning), boosting in a functional space, where the target is ''pseudo-residuals'' instead of Residuals (statistics), residuals as in traditional boosting. It gives a pr ...
).
In explicit regularization, independent of the problem or model, there is always a data term, that corresponds to a likelihood of the measurement, and a regularization term that corresponds to a prior. By combining both using Bayesian statistics, one can compute a posterior, that includes both information sources and therefore stabilizes the estimation process. By trading off both objectives, one chooses to be more aligned to the data or to enforce regularization (to prevent overfitting). There is a whole research branch dealing with all possible regularizations. In practice, one usually tries a specific regularization and then figures out the probability density that corresponds to that regularization to justify the choice. It can also be physically motivated by common sense or intuition.
In machine learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task ( ...
, the data term corresponds to the training data and the regularization is either the choice of the model or modifications to the algorithm. It is always intended to reduce the generalization error
For supervised learning applications in machine learning and statistical learning theory, generalization errorMohri, M., Rostamizadeh A., Talwakar A., (2018) ''Foundations of Machine learning'', 2nd ed., Boston: MIT Press (also known as the out-of- ...
, i.e. the error score with the trained model on the evaluation set (testing data) and not the training data.
One of the earliest uses of regularization is Tikhonov regularization (ridge regression), related to the method of least squares.
Regularization in machine learning
Inmachine learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task ( ...
, a key challenge is enabling models to accurately predict outcomes on unseen data, not just on familiar training data. Regularization is crucial for addressing overfitting
In mathematical modeling, overfitting is "the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit to additional data or predict future observations reliably". An overfi ...
—where a model memorizes training data details but cannot generalize to new data. The goal of regularization is to encourage models to learn the broader patterns within the data rather than memorizing it. Techniques like early stopping
In machine learning, early stopping is a form of Regularization (mathematics), regularization used to avoid overfitting when training a model with an iterative method, such as gradient descent. Such methods update the model to make it better fit th ...
, L1 and L2 regularization, and dropout are designed to prevent overfitting and underfitting, thereby enhancing the model's ability to adapt to and perform well with new data, thus improving model generalization.
Early Stopping
Stops training when validation performance deteriorates, preventing overfitting by halting before the model memorizes training data.L1 and L2 Regularization
Adds penalty terms to the cost function to discourage complex models: * L1 regularization (also calledLASSO
A lasso or lazo ( or ), also called reata or la reata in Mexico, and in the United States riata or lariat (from Mexican Spanish lasso for roping cattle), is a loop of rope designed as a restraint to be thrown around a target and tightened when ...
) leads to sparse models by adding a penalty based on the absolute value of coefficients.
* L2 regularization (also called ridge regression) encourages smaller, more evenly distributed weights by adding a penalty based on the square of the coefficients.
Dropout
In the context of neural networks, the Dropout technique repeatedly ignores random subsets of neurons during training, which simulates the training of multiple neural network architectures at once to improve generalization.Classification
Empirical learning of classifiers (from a finite data set) is always an underdetermined problem, because it attempts to infer a function of any given only examples . A regularization term (or regularizer) is added to aloss function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost ...
:
where is an underlying loss function that describes the cost of predicting when the label is , such as the square loss or hinge loss; and is a parameter which controls the importance of the regularization term. is typically chosen to impose a penalty on the complexity of . Concrete notions of complexity used include restrictions for smoothness
In mathematical analysis, the smoothness of a function is a property measured by the number of continuous derivatives (''differentiability class)'' it has over its domain.
A function of class C^k is a function of smoothness at least ; t ...
and bounds on the vector space norm.
A theoretical justification for regularization is that it attempts to impose Occam's razor
In philosophy, Occam's razor (also spelled Ockham's razor or Ocham's razor; ) is the problem-solving principle that recommends searching for explanations constructed with the smallest possible set of elements. It is also known as the principle o ...
on the solution (as depicted in the figure above, where the green function, the simpler one, may be preferred). From a Bayesian point of view, many regularization techniques correspond to imposing certain prior
The term prior may refer to:
* Prior (ecclesiastical), the head of a priory (monastery)
* Prior convictions, the life history and previous convictions of a suspect or defendant in a criminal case
* Prior probability, in Bayesian statistics
* Prio ...
distributions on model parameters.
Regularization can serve multiple purposes, including learning simpler models, inducing models to be sparse and introducing group structure into the learning problem.
The same idea arose in many fields of science
Science is a systematic discipline that builds and organises knowledge in the form of testable hypotheses and predictions about the universe. Modern science is typically divided into twoor threemajor branches: the natural sciences, which stu ...
. A simple form of regularization applied to integral equation
In mathematical analysis, integral equations are equations in which an unknown function appears under an integral sign. In mathematical notation, integral equations may thus be expressed as being of the form: f(x_1,x_2,x_3,\ldots,x_n ; u(x_1,x_2 ...
s ( Tikhonov regularization) is essentially a trade-off between fitting the data and reducing a norm of the solution. More recently, non-linear regularization methods, including total variation regularization
In signal processing, particularly image processing, total variation denoising, also known as total variation regularization or total variation filtering, is a noise removal process (Filter (signal processing), filter). It is based on the princip ...
, have become popular.
Generalization
Regularization can be motivated as a technique to improve the generalizability of a learned model. The goal of this learning problem is to find a function that fits or predicts the outcome (label) that minimizes the expected error over all possible inputs and labels. The expected error of a function is: where and are the domains of input data and their labels respectively. Typically in learning problems, only a subset of input data and labels are available, measured with some noise. Therefore, the expected error is unmeasurable, and the best surrogate available is the empirical error over the available samples: Without bounds on the complexity of the function space (formally, thereproducing kernel Hilbert space
In functional analysis, a reproducing kernel Hilbert space (RKHS) is a Hilbert space of functions in which point evaluation is a continuous linear functional. Specifically, a Hilbert space H of functions from a set X (to \mathbb or \mathbb) is ...
) available, a model will be learned that incurs zero loss on the surrogate empirical error. If measurements (e.g. of ) were made with noise, this model may suffer from overfitting
In mathematical modeling, overfitting is "the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit to additional data or predict future observations reliably". An overfi ...
and display poor expected error. Regularization introduces a penalty for exploring certain regions of the function space used to build the model, which can improve generalization.
Tikhonov regularization (ridge regression)
These techniques are named for Andrey Nikolayevich Tikhonov, who applied regularization tointegral equation
In mathematical analysis, integral equations are equations in which an unknown function appears under an integral sign. In mathematical notation, integral equations may thus be expressed as being of the form: f(x_1,x_2,x_3,\ldots,x_n ; u(x_1,x_2 ...
s and made important contributions in many other areas.
When learning a linear function , characterized by an unknown vector
Vector most often refers to:
* Euclidean vector, a quantity with a magnitude and a direction
* Disease vector, an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematics a ...
such that , one can add the -norm of the vector to the loss expression in order to prefer solutions with smaller norms. Tikhonov regularization is one of the most common forms. It is also known as ridge regression. It is expressed as:
where would represent samples used for training.
In the case of a general function, the norm of the function in its reproducing kernel Hilbert space
In functional analysis, a reproducing kernel Hilbert space (RKHS) is a Hilbert space of functions in which point evaluation is a continuous linear functional. Specifically, a Hilbert space H of functions from a set X (to \mathbb or \mathbb) is ...
is:
As the norm is differentiable
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non- vertical tangent line at each interior point in ...
, learning can be advanced by gradient descent
Gradient descent is a method for unconstrained mathematical optimization. It is a first-order iterative algorithm for minimizing a differentiable multivariate function.
The idea is to take repeated steps in the opposite direction of the gradi ...
.
Tikhonov-regularized least squares
The learning problem with theleast squares
The method of least squares is a mathematical optimization technique that aims to determine the best fit function by minimizing the sum of the squares of the differences between the observed values and the predicted values of the model. The me ...
loss function and Tikhonov regularization can be solved analytically. Written in matrix form, the optimal is the one for which the gradient of the loss function with respect to is 0.
where the third statement is a first-order condition
In calculus, a derivative test uses the derivatives of a function to locate the critical points of a function and determine whether each point is a local maximum, a local minimum, or a saddle point. Derivative tests can also give information abou ...
.
By construction of the optimization problem, other values of give larger values for the loss function. This can be verified by examining the second derivative
In calculus, the second derivative, or the second-order derivative, of a function is the derivative of the derivative of . Informally, the second derivative can be phrased as "the rate of change of the rate of change"; for example, the secon ...
.
During training, this algorithm takes time
Time is the continuous progression of existence that occurs in an apparently irreversible process, irreversible succession from the past, through the present, and into the future. It is a component quantity of various measurements used to sequ ...
. The terms correspond to the matrix inversion and calculating , respectively. Testing takes time.
Early stopping
Early stopping can be viewed as regularization in time. Intuitively, a training procedure such as gradient descent tends to learn more and more complex functions with increasing iterations. By regularizing for time, model complexity can be controlled, improving generalization. Early stopping is implemented using one data set for training, one statistically independent data set for validation and another for testing. The model is trained until performance on the validation set no longer improves and then applied to the test set.Theoretical motivation in least squares
Consider the finite approximation of Neumann series for an invertible matrix where : This can be used to approximate the analytical solution of unregularized least squares, if is introduced to ensure the norm is less than one. The exact solution to the unregularized least squares learning problem minimizes the empirical error, but may fail. By limiting , the only free parameter in the algorithm above, the problem is regularized for time, which may improve its generalization. The algorithm above is equivalent to restricting the number of gradient descent iterations for the empirical risk with the gradient descent update: The base case is trivial. The inductive case is proved as follows:Regularizers for sparsity
Assume that a dictionary with dimension is given such that a function in the function space can be expressed as: Enforcing a sparsity constraint on can lead to simpler and more interpretable models. This is useful in many real-life applications such as
Enforcing a sparsity constraint on can lead to simpler and more interpretable models. This is useful in many real-life applications such as computational biology
Computational biology refers to the use of techniques in computer science, data analysis, mathematical modeling and Computer simulation, computational simulations to understand biological systems and relationships. An intersection of computer sci ...
. An example is developing a simple predictive test for a disease in order to minimize the cost of performing medical tests while maximizing predictive power.
A sensible sparsity constraint is the norm , defined as the number of non-zero elements in . Solving a regularized learning problem, however, has been demonstrated to be NP-hard
In computational complexity theory, a computational problem ''H'' is called NP-hard if, for every problem ''L'' which can be solved in non-deterministic polynomial-time, there is a polynomial-time reduction from ''L'' to ''H''. That is, assumi ...
.
The norm (see also Norms) can be used to approximate the optimal norm via convex relaxation. It can be shown that the norm induces sparsity. In the case of least squares, this problem is known as LASSO
A lasso or lazo ( or ), also called reata or la reata in Mexico, and in the United States riata or lariat (from Mexican Spanish lasso for roping cattle), is a loop of rope designed as a restraint to be thrown around a target and tightened when ...
in statistics and basis pursuit in signal processing.
 regularization can occasionally produce non-unique solutions. A simple example is provided in the figure when the space of possible solutions lies on a 45 degree line. This can be problematic for certain applications, and is overcome by combining with regularization in elastic net regularization, which takes the following form:
regularization can occasionally produce non-unique solutions. A simple example is provided in the figure when the space of possible solutions lies on a 45 degree line. This can be problematic for certain applications, and is overcome by combining with regularization in elastic net regularization, which takes the following form: