|
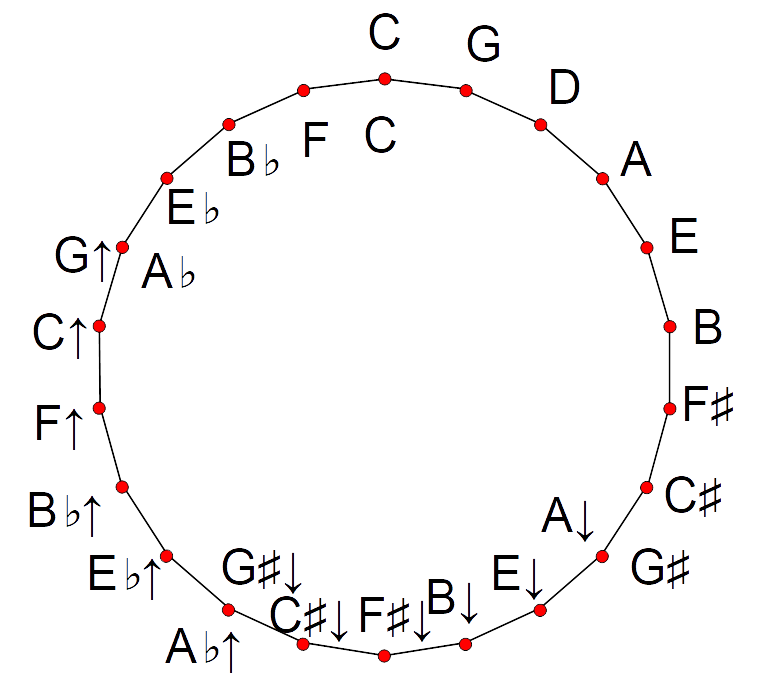
Septimal Semicomma
In music, the septimal semicomma, a seven- limit semicomma, is the ratio 126/125 and is equal to approximately 13.79 cents (). It is also called the ''small septimal comma''Haluska, Jan (2003). ''The Mathematical Theory of Tone Systems'', p.xxvi. . and the ''starling comma'' after its use in starling temperament. Factored into primes it is: 2*3^2*5^*7 Or as simple just intervals: (6/5)^3*(7/6)*(2/1)^ Thus it is the difference between three minor thirds of 6/5 plus a septimal minor third of 7/6 and an octave (2/1). This comma is important to certain tuning systems, such as septimal meantone temperament. A diminished seventh chord consisting of three minor thirds and a subminor third making up an octave is possible in such systems. This characteristic feature of these tuning systems is known as the ''septimal semicomma diminished seventh chord''. In equal temperament It is tempered out in 19 equal temperament and 31 equal temperament, but not in 22 equal temperament, 34 equa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Music
Music is the arrangement of sound to create some combination of Musical form, form, harmony, melody, rhythm, or otherwise Musical expression, expressive content. Music is generally agreed to be a cultural universal that is present in all human societies. Definitions of music vary widely in substance and approach. While scholars agree that music is defined by a small number of elements of music, specific elements, there is no consensus as to what these necessary elements are. Music is often characterized as a highly versatile medium for expressing human creativity. Diverse activities are involved in the creation of music, and are often divided into categories of musical composition, composition, musical improvisation, improvisation, and performance. Music may be performed using a wide variety of musical instruments, including the human voice. It can also be composed, sequenced, or otherwise produced to be indirectly played mechanically or electronically, such as via a music box ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
19 Equal Temperament
In music, 19 equal temperament, called 19 TET, 19 EDO ("Equal Division of the Octave"), 19-ED2 ("Equal Division of 2:1) or 19 Equal temperament, ET, is the musical temperament, tempered scale derived by dividing the octave into 19 equal steps (equal frequency ratios). Each step represents a frequency ratio of , or 63.16 cent (music), cents (). The fact that traditional western music maps unambiguously onto this scale (unless it presupposes 12-EDO enharmonic equivalences) makes it easier to perform such music in this tuning than in many other tunings. 19 EDO is the tuning of the syntonic temperament in which the tempered perfect fifth is equal to 694.737 cents, as shown in Figure 1 (look for the label "19 TET"). On an isomorphic keyboard, the fingering of music composed in 19 EDO is precisely the same as it is in any other syntonic tuning (such as 12-TET, 12 EDO), so long as the notes are "spelled properly" – that is, with no assumption t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
7-limit Tuning And Intervals
7-limit or septimal Musical tuning#Tuning systems, tunings and interval (music), intervals are musical instrument tunings that have a limit (music), limit of seven: the largest prime number, prime factor contained in the interval ratios between pitch (music), pitches is seven. Thus, for example, 50:49 is a 7-limit interval, but 14:11 is not. For example, the greater just minor seventh, 9:5 () is a 5-limit tuning, 5-limit ratio, the harmonic seventh has the ratio 7:4 and is thus a septimal interval. Similarly, the septimal chromatic semitone, 21:20, is a septimal interval as 21÷7=3. The harmonic seventh is used in the barbershop seventh chord and barbershop music, music. () Compositions with septimal tunings include La Monte Young's ''The Well-Tuned Piano'', Ben Johnston (composer), Ben Johnston's String Quartet No. 4, Lou Harrison's ''Incidental Music for Corneille's Cinna'', and Michael Harrison (musician), Michael Harrison's ''Revelation: Music in Pure Intonation''. The Gre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
53 Equal Temperament
In music, 53 equal temperament, called 53 TET, 53 EDO, or 53 ET, is the tempered scale derived by dividing the octave into 53 equal steps (equal frequency ratios) (). Each step represents a frequency ratio of or 22.6415 cents (), an interval sometimes called the Holdrian comma. 53 TET is a tuning of equal temperament in which the tempered perfect fifth is 701.89 cents wide, as shown in Figure 1, and sequential pitches are separated by 22.642 cents. The 53-TET tuning equates to the unison, or ''tempers out'', the intervals known as the schisma, and known as the kleisma. These are both 5 limit intervals, involving only the primes 2, 3, and 5 in their factorization, and the fact that 53 TET tempers out both characterizes it completely as a 5 limit temperament: It is the only regular temperament tempering out both of these intervals, or commas, a fact which seems to have first been recognized by Japanese musi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
41 Equal Temperament
41 may refer to: * 41 (number) * one of the years 41 BC, AD 41, 1941, 2041 Art and entertainment * 41 (film), ''41'' (film), a 2007 documentary about Nicholas O'Neill, the youngest victim of the Station nightclub fire * ''41'', an Australian award-winning science fiction time travel film about a time loop, by Glenn Triggs * ''41'', a 2012 documentary about President George H. W. Bush. * 41 (song), "#41" (song), a song by the Dave Matthews Band * ''Survivor 41'', the 41st installment of CBS's reality program ''Survivor'' * "Forty One", a song by Karma to Burn from the album ''Appalachian Incantation'', 2010 People * George H. W. Bush, or "Bush 41" (to distinguish him from his son, George W. Bush), 41st president of the United States * Nick "41" MacLaren, member of the New Zealand hip hop duo Frontline (band), Frontline * 41 (group), a Brooklyn drill trio Others * HP-41C, a series of calculators made by Hewlett-Packard ** FOCAL (Hewlett-Packard) (Forty-one calculator language), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
34 Equal Temperament
In musical theory, 34 equal temperament, also referred to as 34-TET, 34-EDO or 34-ET, is the tempered tuning derived by dividing the octave into 34 equal-sized steps (equal frequency ratios). Each step represents a frequency ratio of , or 35.29 cents . History and use Unlike divisions of the octave into 19, 31 or 53 steps, which can be considered as being derived from ancient Greek intervals (the greater and lesser diesis and the syntonic comma), division into 34 steps did not arise 'naturally' out of older music theory, although Cyriakus Schneegass proposed a meantone system with 34 divisions based in effect on half a chromatic semitone (the difference between a major third and a minor third, 25:24 or 70.67 cents). Wider interest in the tuning was not seen until modern times, when the computer made possible a systematic search of all possible equal temperaments. While Barbour discusses it,''Tuning and Temperament'', Michigan State College Press, 1951 the first recognition o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
22 Equal Temperament
In music, 22 equal temperament, called 22-TET, 22- EDO, or 22-ET, is the tempered scale derived by dividing the octave into 22 equal steps (equal frequency ratios). Each step represents a frequency ratio of , or 54.55 cents (). When composing with 22-ET, one needs to take into account a variety of considerations. Considering the 5-limit, there is a difference between 3 fifths and the sum of 1 fourth and 1 major third. It means that, starting from C, there are two A's—one 16 steps and one 17 steps away. There is also a difference between a major tone and a minor tone. In C major, the second note (D) will be 4 steps away. However, in A minor, where A is 6 steps below C, the fourth note (D) will be 9 steps above A, so 3 steps above C. So when switching from C major to A minor, one needs to slightly change the D note. These discrepancies arise because, unlike 12-ET, 22-ET does not temper out the syntonic comma of 81/80, but instead exaggerates its size by mapping it to one ste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
31 Equal Temperament
In music, 31 equal temperament, which can also be abbreviated (31 tone ) or (equal division of the octave), also known as tricesimoprimal, is the tempered scale derived by dividing the octave into 31 equally-proportioned steps (equal frequency ratios). Each step represents a frequency ratio of , or 38.71 cents (). is a very good approximation of quarter-comma meantone temperament. More generally, it is a regular diatonic tuning in which the tempered perfect fifth is equal to 696.77 cents, as shown in Figure 1. On an isomorphic keyboard, the fingering of music composed in is precisely the same as it is in any other syntonic tuning (such as so long as the notes are spelled properly—that is, with no assumption of enharmonicity. History and use Division of the octave into 31 steps arose naturally out of Renaissance music theory; the lesser diesis – the ratio of an octave to three major thirds, 128:125 or 41.06 cents – was app ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diminished Seventh Chord
The diminished seventh chord is a four-note chord (a seventh chord) composed of a Root (chord), root note, together with a minor third, a diminished fifth, and a diminished seventh above the root: (1, 3, 5, 7). For example, the diminished seventh chord built on B, commonly Chord names and symbols (popular music), written as B7, has pitches B-D-F-A: : The chord consists of a diminished triad plus the diminished seventh above the root. These four notes form a stack of three Interval (music), intervals which are all minor thirds. Since stacking yet another minor third returns to the root note, the four Inversion (music), inversions of a diminished seventh chord are symmetrical. The Pitch class#Integer notation, integer notation is . Since the diminished seventh interval is enharmonically equivalent to a major sixth, the chord is enharmonically equivalent to (1, 3, 5, 6). The diminished seventh chord occurs as a leading-tone seventh chord in the harm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
7-limit
7-limit or septimal tunings and intervals are musical instrument tunings that have a limit of seven: the largest prime factor contained in the interval ratios between pitches is seven. Thus, for example, 50:49 is a 7-limit interval, but 14:11 is not. For example, the greater just minor seventh, 9:5 () is a 5-limit ratio, the harmonic seventh has the ratio 7:4 and is thus a septimal interval. Similarly, the septimal chromatic semitone, 21:20, is a septimal interval as 21÷7=3. The harmonic seventh is used in the barbershop seventh chord and music. () Compositions with septimal tunings include La Monte Young's ''The Well-Tuned Piano'', Ben Johnston's String Quartet No. 4, Lou Harrison's ''Incidental Music for Corneille's Cinna'', and Michael Harrison's ''Revelation: Music in Pure Intonation''. The Great Highland bagpipe is tuned to a ten-note seven-limit scale: 1:1, 9:8, 5:4, 4:3, 27:20, 3:2, 5:3, 7:4, 16:9, 9:5. In the 2nd century Ptolemy described the septima ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Septimal Meantone Temperament
In music, septimal meantone temperament, also called ''standard septimal meantone'' or simply ''septimal meantone'', refers to the tempering of 7-limit musical intervals by a meantone temperament tuning in the range from fifths flattened by the amount of fifths for 12 equal temperament to those as flat as 19 equal temperament, with 31 equal temperament being a more or less optimal tuning for both the 5- and 7-limits. Choice of temperament Meantone temperament produces a frequency ratio of approximately 5 by means of four fifths, so that the major third (for instance C–E) is obtained from two successive whole tones. Septimal meantone produces the frequency ratio of 56 by ten fifths, so that the interval 7:4 is reached by five successive tones. Hence C–A, not C–B, represents a 7:4 interval in septimal meantone. : There are several slightly adjusted meantone tunings very nearly equivalent to exact quarter comma meantone, which all have good renditions of harmonic seventh i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Septimal Minor Third
Septimal may refer to: *Septimal chromatic semitone, the interval 21:20, about 84.47 cents *Septimal comma, a small musical interval in just intonation divisible by 7 *Septimal diatonic semitone, the interval 15:14, about 119.44 cents *Septimal diesis, an interval with the ratio of 49:48, about 38.71 cents *Septimal kleisma, an interval of approximately 7.7 cents *Septimal major third, the musical interval with a 9:7 ratio of frequencies *Septimal meantone temperament, the tempering of 7-limit musical intervals by a meantone temperament tuning *Septimal minor third, the musical interval exactly or approximately equal to a 7/6 ratio of frequencies *Septimal quarter tone, an interval with the ratio of 36:35, about 48.77 cents *Septimal semicomma, an interval with the ratio 126/125, about 13.79 cents *Septimal sixth-tone (or jubilisma), an interval with the ratio of 50:49, about 34.98 cents *Septimal tritone, the interval 7:5, about 582.51 cents ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |