22 Equal Temperament on:
[Wikipedia]
[Google]
[Amazon]
In music, 22 equal temperament, called 22-TET, 22- EDO, or 22-ET, is the tempered scale derived by dividing the octave into 22 equal steps (equal frequency ratios). Each step represents a frequency ratio of , or 54.55 cents ().
When composing with 22-ET, one needs to take into account a variety of considerations. Considering the 5-limit, there is a difference between 3 fifths and the sum of 1 fourth and 1 major third. It means that, starting from C, there are two A's—one 16 steps and one 17 steps away. There is also a difference between a major tone and a minor tone. In C major, the second note (D) will be 4 steps away. However, in A minor, where A is 6 steps below C, the fourth note (D) will be 9 steps above A, so 3 steps above C. So when switching from C major to A minor, one needs to slightly change the D note. These discrepancies arise because, unlike 12-ET, 22-ET does not temper out the
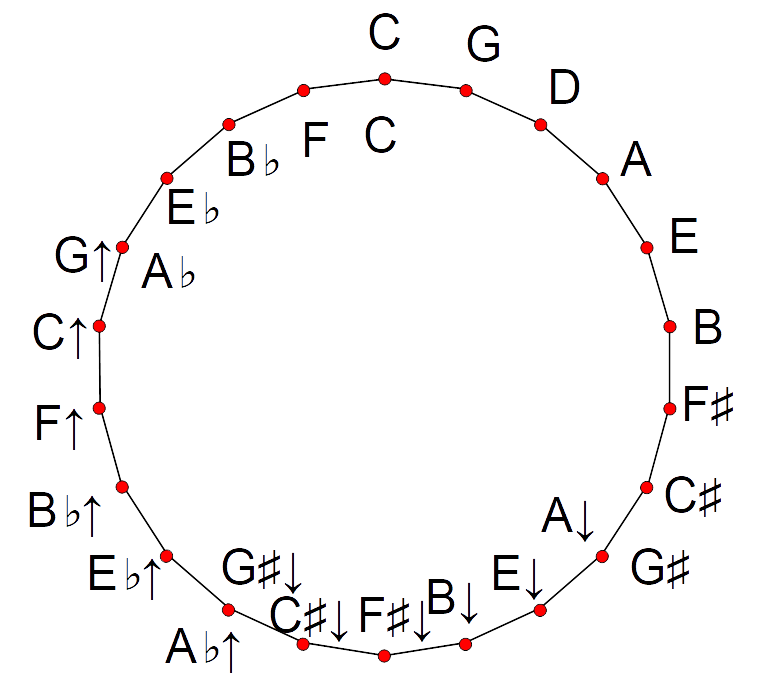
 22-EDO can be notated several ways. The first, Ups And Downs Notation, Accessed 2023-8-12. uses up and down arrows, written as a caret and a lower-case "v", usually in a sans-serif font. One arrow equals one edostep. In note names, the arrows come first, to facilitate chord naming. This yields the following chromatic scale:
C, ^C/D, vC/^D, C/vD,
D, ^D/E, vD/^E, D/vE, E,
F, ^F/G, vF/^G, F/vG,
G, ^G/A, vG/^A, G/vA,
A, ^A/B, vA/^B, A/vB, B, C
The Pythagorean minor chord with 32/27 on C is still named Cm and still spelled C–E–G. But the 5-limit ''up''minor chord uses the upminor 3rd 6/5 and is spelled C–^E–G. This chord is named C^m. Compare with ^Cm (^C–^E–^G).
The second, Quarter Tone Notation, uses half-sharps and half-flats instead of up and down arrows:
C, C, C/D, D,
D, D, D/E, E, E,
F, F, F/G, G,
G, G, G/A, A,
A, A, A/B, B, B, C
However, chords and some enharmonic equivalences are much different than they are in 12-EDO. For example, even though a 5-limit C minor triad is notated as , C major triads are now instead of , and an A minor triad is now even though an A major triad is still . Additionally, while major seconds such as are divided as expected into 4 quarter tones, minor seconds such as and are 1 quarter tone, not 2. Thus is now equivalent to instead of F, is equivalent to instead of E, F is equivalent to , and E is equivalent to . Furthermore, the note a fifth above B is not the expected but rather or , and the note that is a fifth below F is now instead of .
The third, Porcupine Notation, introduces no new accidentals, but significantly changes chord spellings (e.g. the 5-limit major triad is now C–E–G). In addition, enharmonic equivalences from 12-EDO are no longer valid. This yields the following chromatic scale:
C, C, D,
D, D, E,
E, E, F,
F, F, G,
G, G, G/A, A,
A, A, B,
B, B, C, C
22-EDO can be notated several ways. The first, Ups And Downs Notation, Accessed 2023-8-12. uses up and down arrows, written as a caret and a lower-case "v", usually in a sans-serif font. One arrow equals one edostep. In note names, the arrows come first, to facilitate chord naming. This yields the following chromatic scale:
C, ^C/D, vC/^D, C/vD,
D, ^D/E, vD/^E, D/vE, E,
F, ^F/G, vF/^G, F/vG,
G, ^G/A, vG/^A, G/vA,
A, ^A/B, vA/^B, A/vB, B, C
The Pythagorean minor chord with 32/27 on C is still named Cm and still spelled C–E–G. But the 5-limit ''up''minor chord uses the upminor 3rd 6/5 and is spelled C–^E–G. This chord is named C^m. Compare with ^Cm (^C–^E–^G).
The second, Quarter Tone Notation, uses half-sharps and half-flats instead of up and down arrows:
C, C, C/D, D,
D, D, D/E, E, E,
F, F, F/G, G,
G, G, G/A, A,
A, A, A/B, B, B, C
However, chords and some enharmonic equivalences are much different than they are in 12-EDO. For example, even though a 5-limit C minor triad is notated as , C major triads are now instead of , and an A minor triad is now even though an A major triad is still . Additionally, while major seconds such as are divided as expected into 4 quarter tones, minor seconds such as and are 1 quarter tone, not 2. Thus is now equivalent to instead of F, is equivalent to instead of E, F is equivalent to , and E is equivalent to . Furthermore, the note a fifth above B is not the expected but rather or , and the note that is a fifth below F is now instead of .
The third, Porcupine Notation, introduces no new accidentals, but significantly changes chord spellings (e.g. the 5-limit major triad is now C–E–G). In addition, enharmonic equivalences from 12-EDO are no longer valid. This yields the following chromatic scale:
C, C, D,
D, D, E,
E, E, F,
F, F, G,
G, G, G/A, A,
A, A, B,
B, B, C, C
 The table below gives the sizes of some common intervals in 22 equal temperament. Intervals shown with a shaded background—such as the septimal tritones—are more than 1/4 of a step (approximately 13.6 cents) out of tune, when compared to the just ratios they approximate.
The table below gives the sizes of some common intervals in 22 equal temperament. Intervals shown with a shaded background—such as the septimal tritones—are more than 1/4 of a step (approximately 13.6 cents) out of tune, when compared to the just ratios they approximate.
Erlich, Paul, "Tuning, Tonality, and Twenty-Two Tone Temperament"
''William A. Sethares''.
Pachelbel's Canon in 22edo (MIDI)
''Herman Miller'' {{Musical tuning Equal temperaments Microtonality
syntonic comma
In music theory
Music theory is the study of theoretical frameworks for understanding the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory": The first i ...
of 81/80, but instead exaggerates its size by mapping it to one step.
In the 7-limit, the septimal minor seventh (7/4) can be distinguished from the sum of a fifth (3/2) and a minor third (6/5), and the septimal subminor third (7/6) is different from the minor third (6/5). This mapping tempers out the septimal comma
A septimal comma is a small interval (music), musical interval in just intonation that contains the number 7, seven in its prime factorization. There is more than one such interval, so the term ''septimal comma'' is ambiguous, but it most commonl ...
of 64/63, which allows 22-ET to function as a "Superpythagorean" system where four stacked fifths are equated with the septimal major third (9/7) rather than the usual pental third of 5/4. This system is a "mirror image" of septimal meantone
In music, septimal meantone temperament, also called ''standard septimal meantone'' or simply ''septimal meantone'', refers to the tempering of 7-limit musical intervals by a meantone temperament tuning in the range from fifths flattened by the a ...
in many ways: meantone systems tune the fifth flat so that intervals of 5 are simple while intervals of 7 are complex, superpythagorean systems have the fifth tuned sharp so that intervals of 7 are simple while intervals of 5 are complex. The enharmonic structure is also reversed: sharps are sharper than flats, similar to Pythagorean tuning (and by extension 53 equal temperament
In music, 53 equal temperament, called 53 TET, 53 EDO, or 53 ET, is the tempered scale derived by dividing the octave into 53 equal steps (equal frequency ratios) (). Each step represents a frequency ratio of or 22.64 ...
), but to a greater degree.
Finally, 22-ET has a good approximation of the 11th harmonic, and is in fact the smallest equal temperament to be consistent in the 11-limit.
The net effect is that 22-ET allows (and to some extent even forces) the exploration of new musical territory, while still having excellent approximations of common practice consonances.
History and use
The idea of dividing the octave into 22 steps of equal size seems to have originated with nineteenth-century music theorist RHM Bosanquet. Inspired by the use of a 22-tone unequal division of the octave in the music theory of India, Bosanquet noted that a 22-tone equal division was capable of representing 5-limit music with tolerable accuracy. In this he was followed in the twentieth century by theorist José Würschmidt, who noted it as a possible next step after19 equal temperament
In music, 19 equal temperament, called 19 TET, 19 EDO ("Equal Division of the Octave"), 19-ED2 ("Equal Division of 2:1) or 19 Equal temperament, ET, is the musical temperament, tempered scale derived by dividing the octave into 19 equal steps ...
, and J. Murray Barbour
James Murray Barbour (1897–1970) is an American acoustician, musicologist, and composer best known for his work ''Tuning and Temperament: A Historical Survey'' (1951, 2d ed. 1953). As the opening of the work describes, it is based upon his unpub ...
in his survey of tuning history, ''Tuning and Temperament''.Barbour, James Murray, ''Tuning and temperament, a historical survey'', East Lansing, Michigan State College Press, 1953 1951
Events
January
* January 4 – Korean War: Third Battle of Seoul – Chinese and North Korean forces capture Seoul for the second time (having lost the Second Battle of Seoul in September 1950).
* January 9 – The Government of the Uni ...
Contemporary advocates of 22 equal temperament include music theorist Paul Erlich and electronic music composer Sevish.
Notation

 22-EDO can be notated several ways. The first, Ups And Downs Notation, Accessed 2023-8-12. uses up and down arrows, written as a caret and a lower-case "v", usually in a sans-serif font. One arrow equals one edostep. In note names, the arrows come first, to facilitate chord naming. This yields the following chromatic scale:
C, ^C/D, vC/^D, C/vD,
D, ^D/E, vD/^E, D/vE, E,
F, ^F/G, vF/^G, F/vG,
G, ^G/A, vG/^A, G/vA,
A, ^A/B, vA/^B, A/vB, B, C
The Pythagorean minor chord with 32/27 on C is still named Cm and still spelled C–E–G. But the 5-limit ''up''minor chord uses the upminor 3rd 6/5 and is spelled C–^E–G. This chord is named C^m. Compare with ^Cm (^C–^E–^G).
The second, Quarter Tone Notation, uses half-sharps and half-flats instead of up and down arrows:
C, C, C/D, D,
D, D, D/E, E, E,
F, F, F/G, G,
G, G, G/A, A,
A, A, A/B, B, B, C
However, chords and some enharmonic equivalences are much different than they are in 12-EDO. For example, even though a 5-limit C minor triad is notated as , C major triads are now instead of , and an A minor triad is now even though an A major triad is still . Additionally, while major seconds such as are divided as expected into 4 quarter tones, minor seconds such as and are 1 quarter tone, not 2. Thus is now equivalent to instead of F, is equivalent to instead of E, F is equivalent to , and E is equivalent to . Furthermore, the note a fifth above B is not the expected but rather or , and the note that is a fifth below F is now instead of .
The third, Porcupine Notation, introduces no new accidentals, but significantly changes chord spellings (e.g. the 5-limit major triad is now C–E–G). In addition, enharmonic equivalences from 12-EDO are no longer valid. This yields the following chromatic scale:
C, C, D,
D, D, E,
E, E, F,
F, F, G,
G, G, G/A, A,
A, A, B,
B, B, C, C
22-EDO can be notated several ways. The first, Ups And Downs Notation, Accessed 2023-8-12. uses up and down arrows, written as a caret and a lower-case "v", usually in a sans-serif font. One arrow equals one edostep. In note names, the arrows come first, to facilitate chord naming. This yields the following chromatic scale:
C, ^C/D, vC/^D, C/vD,
D, ^D/E, vD/^E, D/vE, E,
F, ^F/G, vF/^G, F/vG,
G, ^G/A, vG/^A, G/vA,
A, ^A/B, vA/^B, A/vB, B, C
The Pythagorean minor chord with 32/27 on C is still named Cm and still spelled C–E–G. But the 5-limit ''up''minor chord uses the upminor 3rd 6/5 and is spelled C–^E–G. This chord is named C^m. Compare with ^Cm (^C–^E–^G).
The second, Quarter Tone Notation, uses half-sharps and half-flats instead of up and down arrows:
C, C, C/D, D,
D, D, D/E, E, E,
F, F, F/G, G,
G, G, G/A, A,
A, A, A/B, B, B, C
However, chords and some enharmonic equivalences are much different than they are in 12-EDO. For example, even though a 5-limit C minor triad is notated as , C major triads are now instead of , and an A minor triad is now even though an A major triad is still . Additionally, while major seconds such as are divided as expected into 4 quarter tones, minor seconds such as and are 1 quarter tone, not 2. Thus is now equivalent to instead of F, is equivalent to instead of E, F is equivalent to , and E is equivalent to . Furthermore, the note a fifth above B is not the expected but rather or , and the note that is a fifth below F is now instead of .
The third, Porcupine Notation, introduces no new accidentals, but significantly changes chord spellings (e.g. the 5-limit major triad is now C–E–G). In addition, enharmonic equivalences from 12-EDO are no longer valid. This yields the following chromatic scale:
C, C, D,
D, D, E,
E, E, F,
F, F, G,
G, G, G/A, A,
A, A, B,
B, B, C, C
Interval size
See also
* Musical temperament *Equal temperament
An equal temperament is a musical temperament or Musical tuning#Tuning systems, tuning system that approximates Just intonation, just intervals by dividing an octave (or other interval) into steps such that the ratio of the frequency, frequencie ...
References
External links
Erlich, Paul, "Tuning, Tonality, and Twenty-Two Tone Temperament"
''William A. Sethares''.
Pachelbel's Canon in 22edo (MIDI)
''Herman Miller'' {{Musical tuning Equal temperaments Microtonality