|
Radial Speed
The radial velocity or line-of-sight velocity of a target with respect to an observer is the rate of change of the vector displacement between the two points. It is formulated as the vector projection of the target-observer relative velocity onto the relative direction or line-of-sight (LOS) connecting the two points. The radial speed or range rate is the temporal rate of the distance or range between the two points. It is a signed scalar quantity, formulated as the scalar projection of the relative velocity vector onto the LOS direction. Equivalently, radial speed equals the norm of the radial velocity, modulo the sign. In astronomy, the point is usually taken to be the observer on Earth, so the radial velocity then denotes the speed with which the object moves away from the Earth (or approaches it, for a negative radial velocity). Formulation Given a differentiable vector \mathbf r \in \mathbb^3 defining the instantaneous relative position of a target with respect to a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relative Position
In geometry, a position or position vector, also known as location vector or radius vector, is a Euclidean vector that represents a point ''P'' in space. Its length represents the distance in relation to an arbitrary reference origin ''O'', and its direction represents the angular orientation with respect to given reference axes. Usually denoted x, r, or s, it corresponds to the straight line segment from ''O'' to ''P''. In other words, it is the displacement or translation that maps the origin to ''P'': :\mathbf=\overrightarrow. The term position vector is used mostly in the fields of differential geometry, mechanics and occasionally vector calculus. Frequently this is used in two-dimensional or three-dimensional space, but can be easily generalized to Euclidean spaces and affine spaces of any dimension.Keller, F. J., Gettys, W. E. et al. (1993), p. 28–29. Relative position The relative position of a point ''Q'' with respect to point ''P'' is the Euclidean vector res ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallax
Parallax is a displacement or difference in the apparent position of an object viewed along two different sightline, lines of sight and is measured by the angle or half-angle of inclination between those two lines. Due to perspective (graphical), foreshortening, nearby objects show a larger parallax than farther objects, so parallax can be used to determine distances. To measure large distances, such as the distance of a planet or a star from Earth, astronomers use the principle of parallax. Here, the term ''Stellar parallax, parallax'' is the semi-angle of inclination between two sight-lines to the star, as observed when Earth is on opposite sides of the Sun in its orbit. These distances form the lowest rung of what is called "the cosmic distance ladder", the first in a succession of methods by which astronomers determine the distances to celestial objects, serving as a basis for other distance measurements in astronomy forming the higher rungs of the ladder. Because parallax ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Secular Variation
The secular variation of a time series is its long-term, non-periodic variation (see '' Decomposition of time series''). Whether a variation is perceived as secular or not depends on the available timescale: a variation that is secular over a timescale of centuries may be a segment of what is, over a timescale of millions of years, a periodic variation. Natural quantities often have both periodic and secular variations. Secular variation is sometimes called secular trend or secular drift when the emphasis is on a linear long-term trend. The term is used wherever time series are applicable in history, economics, operations research, biological anthropology, and astronomy (particularly celestial mechanics) such as VSOP (planets). Etymology The word ''secular'', from the Latin root ''saecularis'' ("of an age, occurring once in an age"), has two basic meanings: I. Of or pertaining to the world (from which secularity is derived), and II. Of or belonging to an age or long period. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astrometric
Astrometry is a branch of astronomy that involves precise measurements of the positions and movements of stars and other celestial bodies. It provides the kinematics and physical origin of the Solar System and this galaxy, the Milky Way. History The history of astrometry is linked to the history of star catalogues, which gave astronomers reference points for objects in the sky so they could track their movements. This can be dated back to the ancient Greek astronomer Hipparchus, who around 190 BC used the catalogue of his predecessors Timocharis and Aristillus to discover Earth's precession. In doing so, he also developed the brightness scale still in use today. Hipparchus compiled a catalogue with at least 850 stars and their positions. Hipparchus's successor, Ptolemy, included a catalogue of 1,022 stars in his work the '' Almagest'', giving their location, coordinates, and brightness. In the 10th century, the Iranian astronomer Abd al-Rahman al-Sufi carried out observation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosmology
Cosmology () is a branch of physics and metaphysics dealing with the nature of the universe, the cosmos. The term ''cosmology'' was first used in English in 1656 in Thomas Blount's ''Glossographia'', with the meaning of "a speaking of the world". In 1731, German philosopher Christian Wolff used the term cosmology in Latin (''cosmologia'') to denote a branch of metaphysics that deals with the general nature of the physical world. Religious or mythological cosmology is a body of beliefs based on mythological, religious, and esoteric literature and traditions of creation myths and eschatology. In the science of astronomy, cosmology is concerned with the study of the chronology of the universe. Physical cosmology is the study of the observable universe's origin, its large-scale structures and dynamics, and the ultimate fate of the universe, including the laws of science that govern these areas. It is investigated by scientists, including astronomers and physicists, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theory Of Relativity
The theory of relativity usually encompasses two interrelated physics theories by Albert Einstein: special relativity and general relativity, proposed and published in 1905 and 1915, respectively. Special relativity applies to all physical phenomena in the absence of gravity. General relativity explains the law of gravitation and its relation to the forces of nature. It applies to the cosmological and astrophysical realm, including astronomy. The theory transformed theoretical physics and astronomy during the 20th century, superseding a 200-year-old theory of mechanics created primarily by Isaac Newton. It introduced concepts including 4-dimensional spacetime as a unified entity of space and time, relativity of simultaneity, kinematic and gravitational time dilation, and length contraction. In the field of physics, relativity improved the science of elementary particles and their fundamental interactions, along with ushering in the nuclear age. With relativity, cosmolog ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Doppler Spectroscopy
Doppler spectroscopy (also known as the radial-velocity method, or colloquially, the wobble method) is an indirect method for finding extrasolar planets and brown dwarfs from radial-velocity measurements via observation of Doppler shifts in the spectrum of the planet's parent star. As of June 2025, over 1,100 known extrasolar planets (about 19.0% of the total) have been discovered using Doppler spectroscopy. History Otto Struve proposed in 1952 the use of powerful spectrographs to detect distant planets. He described how a very large planet, as large as Jupiter, for example, would cause its parent star to wobble slightly as the two objects orbit around their center of mass. He predicted that the small Doppler shifts to the light emitted by the star, caused by its continuously varying radial velocity, would be detectable by the most sensitive spectrographs as tiny redshifts and blueshifts in the star's emission. However, the technology of the time produced radial-veloc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiparallel Vector
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Euclidean vectors can be added and scaled to form a vector space. A ''vector quantity'' is a vector-valued physical quantity, including units of measurement and possibly a support, formulated as a ''directed line segment''. A vector is frequently depicted graphically as an arrow connecting an ''initial point'' ''A'' with a ''terminal point'' ''B'', and denoted by \stackrel \longrightarrow. A vector is what is needed to "carry" the point ''A'' to the point ''B''; the Latin word means 'carrier'. It was first used by 18th century astronomers investigating planetary revolution around the Sun. The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from ''A'' to ''B''. Many algebraic operations on real numbers su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
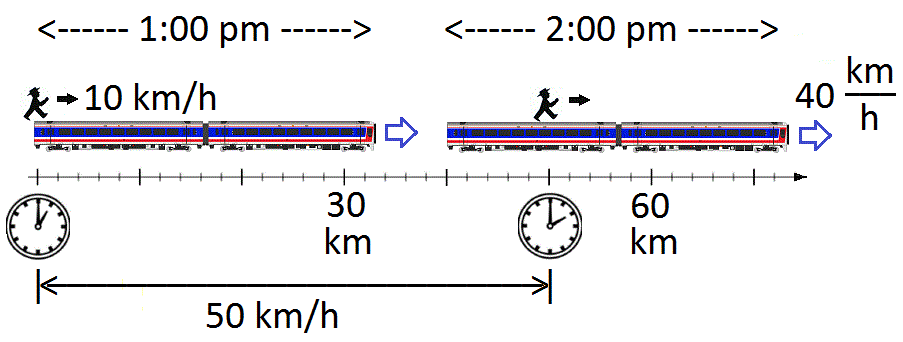
Relative Speed
The relative velocity of an object ''B'' relative to an observer ''A'', denoted \mathbf v_ (also \mathbf v_ or \mathbf v_), is the velocity vector (physics), vector of ''B'' measured in the rest frame of ''A''. The relative speed v_ = \, \mathbf v_\, is the vector norm of the relative velocity. Classical mechanics In one dimension (non-relativistic) We begin with relative motion in the classical mechanics, classical, (or non-special relativity, relativistic, or the Classical mechanics, Newtonian approximation) that all speeds are much less than the speed of light. This limit is associated with the Galilean transformation. The figure shows a man on top of a train, at the back edge. At 1:00 pm he begins to walk forward at a walking speed of 10 km/h (kilometers per hour). The train is moving at 40 km/h. The figure depicts the man and train at two different times: first, when the journey began, and also one hour later at 2:00 pm. The figure suggests that the man i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Vector
In mathematics, a unit vector in a normed vector space is a Vector (mathematics and physics), vector (often a vector (geometry), spatial vector) of Norm (mathematics), length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in \hat (pronounced "v-hat"). The term ''normalized vector'' is sometimes used as a synonym for ''unit vector''. The normalized vector û of a non-zero vector u is the unit vector in the direction of u, i.e., :\mathbf = \frac=(\frac, \frac, ... , \frac) where ‖u‖ is the Norm (mathematics), norm (or length) of u and \, \mathbf\, = (u_1, u_2, ..., u_n). The proof is the following: \, \mathbf\, =\sqrt=\sqrt=\sqrt=1 A unit vector is often used to represent direction (geometry), directions, such as normal directions. Unit vectors are often chosen to form the basis (linear algebra), basis of a vector space, and every vector in the space may be written as a linear combination form of unit vectors. Orthogonal coordinates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chain Rule
In calculus, the chain rule is a formula that expresses the derivative of the Function composition, composition of two differentiable functions and in terms of the derivatives of and . More precisely, if h=f\circ g is the function such that h(x)=f(g(x)) for every , then the chain rule is, in Lagrange's notation, h'(x) = f'(g(x)) g'(x). or, equivalently, h'=(f\circ g)'=(f'\circ g)\cdot g'. The chain rule may also be expressed in Leibniz's notation. If a variable depends on the variable , which itself depends on the variable (that is, and are dependent variables), then depends on as well, via the intermediate variable . In this case, the chain rule is expressed as \frac = \frac \cdot \frac, and \left.\frac\_ = \left.\frac\_ \cdot \left. \frac\_ , for indicating at which points the derivatives have to be evaluated. In integral, integration, the counterpart to the chain rule is the substitution rule. Intuitive explanation Intuitively, the chain rule states that knowing t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |