|
Quantum Depolarizing Channel
A quantum depolarizing channel is a model for quantum noise in quantum systems. The d-dimensional depolarizing channel can be viewed as a completely positive trace-preserving map \Delta_\lambda, depending on one parameter \lambda, which maps a state \rho onto a linear combination of itself and the maximally mixed state, :\Delta_\lambda(\rho)=(1-\lambda)\rho+\fracI. The condition of complete positivity requires \lambda to satisfy the bounds :0\le\lambda\le 1+\frac. Qubit Channel The single qubit depolarizing channel has operator-sum representation on a density matrix \rho given by :\Delta_\lambda(\rho) = \sum_^ K_i \rho K_i^\dagger, where K_i are the Kraus operators given by :K_0 = \sqrt I, K_1 = \sqrt X, K_2 = \sqrt Y, K_3 = \sqrt Z and \ are the Pauli matrices. The trace preserving condition is satisfied by the fact that \sum_K_i ^\dagger K_i = I. Geometrically the depolarizing channel \Delta_\lambda can be interpreted as a uniform contraction of the Bloch sphere, paramete ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Noise
Noise is unwanted sound considered unpleasant, loud or disruptive to hearing. From a physics standpoint, there is no distinction between noise and desired sound, as both are vibrations through a medium, such as air or water. The difference arises when the brain receives and perceives a sound. Acoustic noise is any sound in the acoustic domain, either deliberate (e.g., music or speech) or unintended. In contrast, noise in electronics may not be audible to the human ear and may require instruments for detection. In audio engineering, noise can refer to the unwanted residual electronic noise signal that gives rise to acoustic noise heard as a hiss. This signal noise is commonly measured using A-weighting or ITU-R 468 weighting. In experimental sciences, noise can refer to any random fluctuations of data that hinders perception of a signal. Measurement Sound is measured based on the amplitude and frequency of a sound wave. Amplitude measures how forceful the wave is. The e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
HSW Theorem
HSW may refer to: * Hall School Wimbledon, in Wimbledon, London, England * Harvard Business School, Stanford Graduate School of Business and Wharton School of the University of Pennsylvania, often considered the three top business schools worldwide and referred to together when referencing their cachet or desirability * Haswell (microarchitecture) * Health and Safety at Work etc. Act 1974, of the United Kingdom * Hellenic Seaways, a Greek ferry operator * Heswall railway station, in England * Historical Society of Washington, D.C. * Howard Scott Warshaw (born 1957), American game designer * HowStuffWorks, a website * HSW International, now Remark Media * HSW Łuczniczka, a stadium in Bydgoszcz, Poland * Hungry Shark World, a video game published by Ubisoft. * Huta Stalowa Wola Huta Stalowa Wola (HSW SA) is a defense contractor that operates a steel mill in the city of Stalowa Wola, Poland. It is a major producer of military equipment and one of the largest heavy construct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
IEEE Transactions On Information Theory
''IEEE Transactions on Information Theory'' is a monthly peer-reviewed scientific journal published by the IEEE Information Theory Society. It covers information theory and the mathematics of communications. It was established in 1953 as ''IRE Transactions on Information Theory''. The editor-in-chief is Muriel Médard (Massachusetts Institute of Technology). As of 2007, the journal allows the posting of preprints on arXiv. According to Jack van Lint, it is the leading research journal in the whole field of coding theory. A 2006 study using the PageRank network analysis algorithm found that, among hundreds of computer science-related journals, ''IEEE Transactions on Information Theory'' had the highest ranking and was thus deemed the most prestigious. ''ACM Computing Surveys'', with the highest impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unital Qubit Channels
Unital may refer to: * A unital algebra – an algebra that contains a multiplicative identity element. * A geometric unital – a block design for integer . * A unital algebraic structure In mathematics, an algebraic structure consists of a nonempty set ''A'' (called the underlying set, carrier set or domain), a collection of operations on ''A'' (typically binary operations such as addition and multiplication), and a finite set ..., such as a unital magma. * A unital map on C*-algebras – a map that preserves the identity element. {{dab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lieb–Thirring Inequality
In mathematics and physics, Lieb–Thirring inequalities provide an upper bound on the sums of powers of the negative eigenvalues of a Schrödinger operator in terms of integrals of the potential. They are named after E. H. Lieb and W. E. Thirring. The inequalities are useful in studies of quantum mechanics and differential equations and imply, as a corollary, a lower bound on the kinetic energy of N quantum mechanical particles that plays an important role in the proof of stability of matter. Statement of the inequalities For the Schrödinger operator -\Delta+V(x)=-\nabla^2+V(x) on \Reals^n with real-valued potential V(x) : \Reals^n \to \Reals, the numbers \lambda_1\le\lambda_2\le\dots\le0 denote the (not necessarily finite) sequence of negative eigenvalues. Then, for \gamma and n satisfying one of the conditions :\begin \gamma\ge\frac12&,\,n=1,\\ \gamma>0&,\,n=2,\\ \gamma\ge0&,\,n\ge3, \end there exists a constant L_, which only depends on \gamma and n, such that whe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
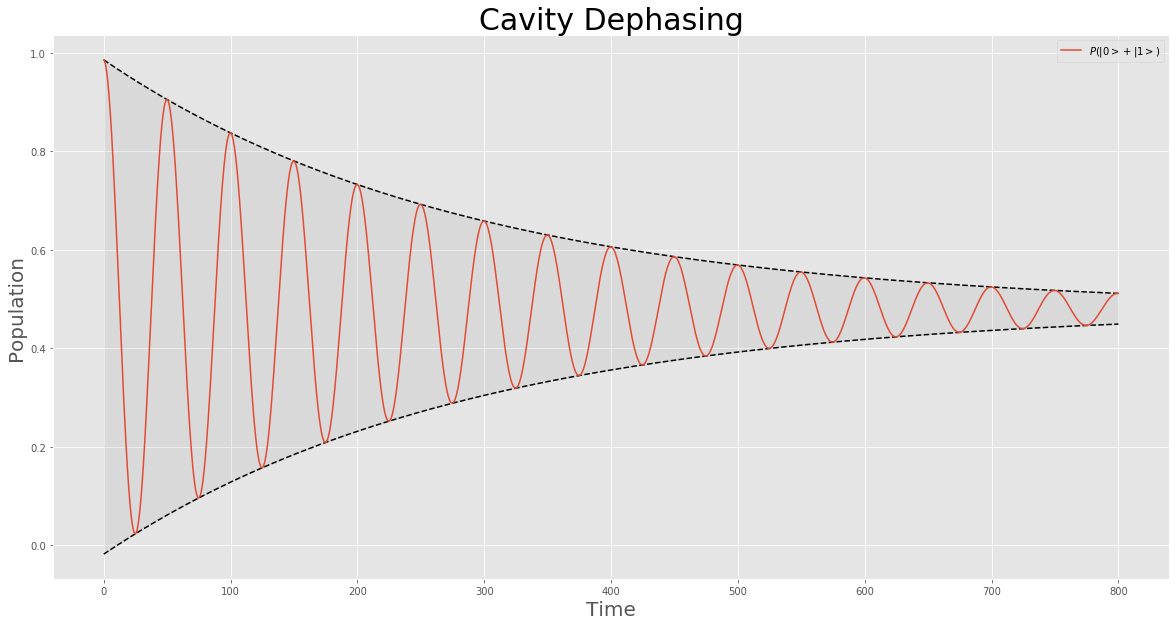
Dephasing
In physics, dephasing is a mechanism that recovers classical behaviour from a quantum system. It refers to the ways in which coherence caused by perturbation decays over time, and the system returns to the state before perturbation. It is an important effect in molecular and atomic spectroscopy, and in the condensed matter physics of mesoscopic devices. The reason can be understood by describing the conduction in metals as a classical phenomenon with quantum effects all embedded into an effective mass that can be computed quantum mechanically, as also happens to resistance that can be seen as a scattering effect of conduction electrons. When the temperature is lowered and the dimensions of the device are meaningfully reduced, this classical behaviour should disappear and the laws of quantum mechanics should govern the behavior of conducting electrons seen as waves that move ballistically inside the conductor without any kind of dissipation. Most of the time this is what one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
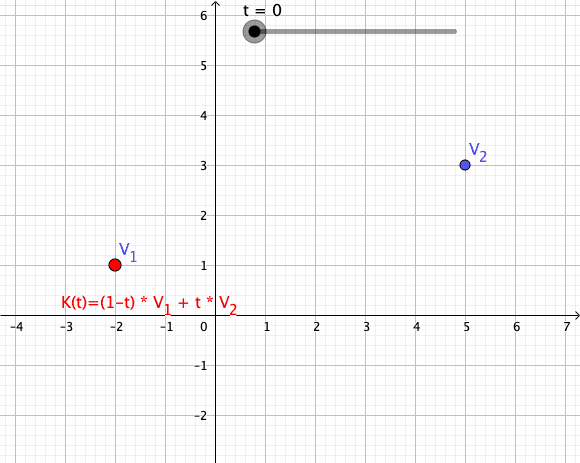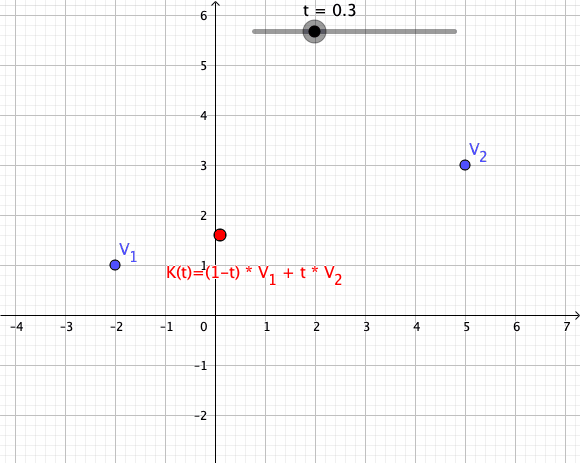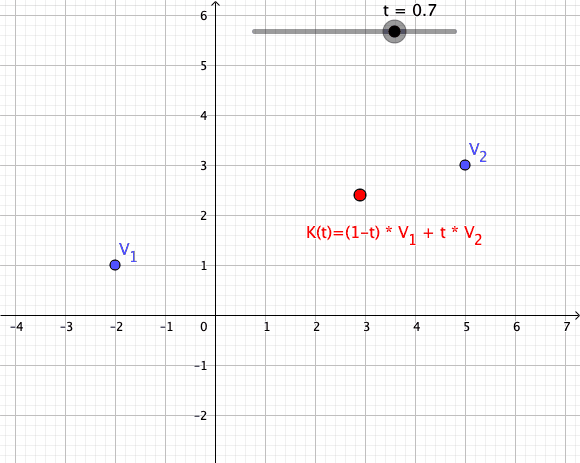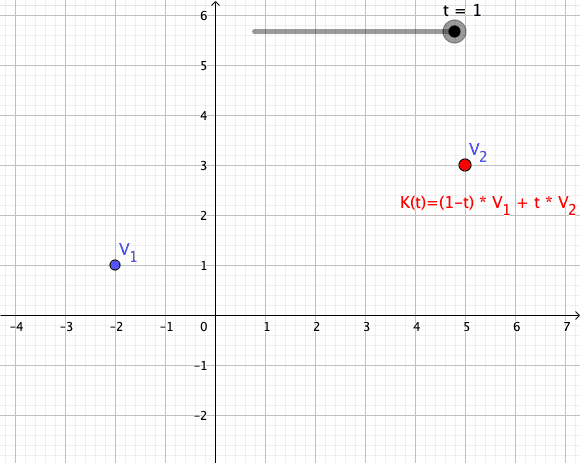
Convex Combination
In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form :\alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is id ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum Output P-norm
In mathematical analysis, the maxima and minima (the respective plurals of maximum and minimum) of a function, known collectively as extrema (the plural of extremum), are the largest and smallest value of the function, either within a given range (the ''local'' or ''relative'' extrema), or on the entire domain (the ''global'' or ''absolute'' extrema). Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions. As defined in set theory, the maximum and minimum of a set are the greatest and least elements in the set, respectively. Unbounded infinite sets, such as the set of real numbers, have no minimum or maximum. Definition A real-valued function ''f'' defined on a domain ''X'' has a global (or absolute) maximum point at ''x''∗, if for all ''x'' in ''X''. Similarly, the function has a global (or absolute) minimum point at ''x''∗, if for all ''x'' in ''X''. The value of the functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Holevo Information
Holevo's theorem is an important limitative theorem in quantum computing, an interdisciplinary field of physics and computer science. It is sometimes called Holevo's bound, since it establishes an upper bound to the amount of information that can be known about a quantum state (accessible information). It was published by Alexander Holevo in 1973. Accessible information As for several concepts in quantum information theory, accessible information is best understood in terms of a 2-party communication. So we introduce two parties, Alice and Bob. Alice has a ''classical'' random variable ''X'', which can take the values with corresponding probabilities . Alice then prepares a quantum state, represented by the density matrix ''ρX'' chosen from a set , and gives this state to Bob. Bob's goal is to find the value of ''X'', and in order to do that, he performs a measurement on the state ''ρ''''X'', obtaining a classical outcome, which we denote with ''Y''. In this context, the amount ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bloch Sphere
In quantum mechanics and computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system (qubit), named after the physicist Felix Bloch. Quantum mechanics is mathematically formulated in Hilbert space or projective Hilbert space. The pure states of a quantum system correspond to the one-dimensional subspaces of the corresponding Hilbert space (and the "points" of the projective Hilbert space). For a two-dimensional Hilbert space, the space of all such states is the complex projective line \mathbb^1. This is the Bloch sphere, which can be mapped to the Riemann sphere. The Bloch sphere is a unit 2-sphere, with antipodal points corresponding to a pair of mutually orthogonal state vectors. The north and south poles of the Bloch sphere are typically chosen to correspond to the standard basis vectors , 0\rangle and , 1\rangle, respectively, which in turn might correspond e.g. to the spin-up and spin-down states of an electr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Channel
In quantum information theory, a quantum channel is a communication channel which can transmit quantum information, as well as classical information. An example of quantum information is the state of a qubit. An example of classical information is a text document transmitted over the Internet. More formally, quantum channels are completely positive (CP) trace-preserving maps between spaces of operators. In other words, a quantum channel is just a quantum operation viewed not merely as the reduced dynamics of a system but as a pipeline intended to carry quantum information. (Some authors use the term "quantum operation" to also include trace-decreasing maps while reserving "quantum channel" for strictly trace-preserving maps.) Memoryless quantum channel We will assume for the moment that all state spaces of the systems considered, classical or quantum, are finite-dimensional. The memoryless in the section title carries the same meaning as in classical information theory: th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |