|
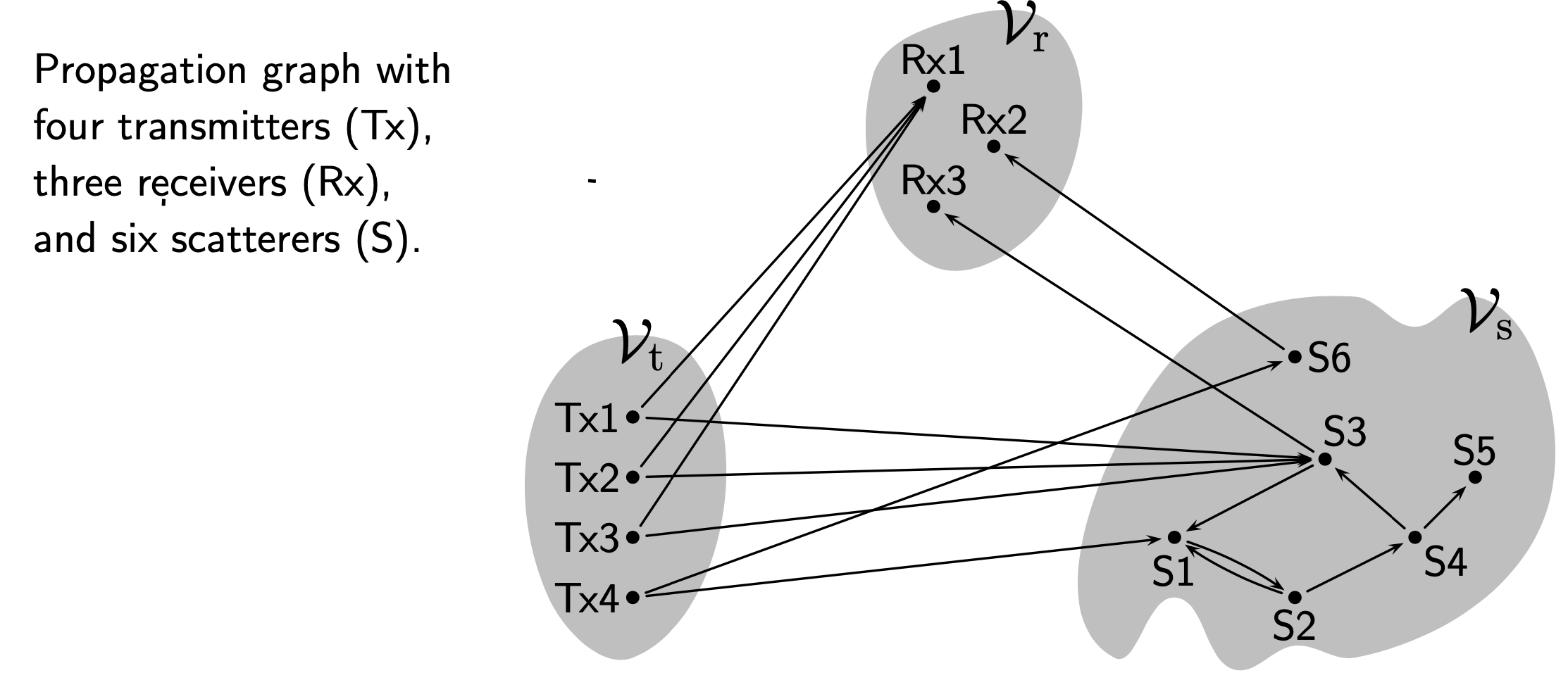
Propagation Graph
Propagation graphs are a mathematical modelling method for radio propagation channels. A propagation graph is a Signal-flow graph, signal flow graph in which vertices represent transmitters, receivers or scatterers. Edges in the graph model propagation conditions between vertices. Propagation graph models were initially developed by Troels Pedersen, et al. for multipath propagation in scenarios with multiple scattering, such as indoor radio propagation. It has later been applied in many other scenarios. Mathematical definition A propagation graph is a simple directed graph \mathcal G = (\mathcal V, \mathcal E) with vertex set \mathcal V and edge set \mathcal E. The vertices models objects in the propagation scenario. The vertex set \mathcal V is split into three disjoint sets as \mathcal V = \mathcal V_t \cup \mathcal V_r \cup\mathcal V_s where \mathcal V_t is the set of transmitters, \mathcal V_r is the set of receivers and \mathcal V_s is the set of objects named "sc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Born Series
The Born series is the expansion of different scattering quantities in quantum scattering theory in the powers of the interaction potential V (more precisely in powers of G_0 V, where G_0 is the free particle Green's operator). It is closely related to Born approximation, which is the first order term of the Born series. The series can formally be understood as power series introducing the coupling constant by substitution V \to \lambda V . The speed of convergence and radius of convergence of the Born series are related to eigenvalues of the operator G_0 V . In general the first few terms of the Born series are good approximation to the expanded quantity for "weak" interaction V and large collision energy. Born series for scattering states The Born series for the scattering states reads : , \psi\rangle = , \phi \rangle + G_0(E) V , \phi\rangle + _0(E) V2 , \phi\rangle + _0(E) V3 , \phi\rangle + \dots It can be derived by iterating the Lippmann–Schwinger equation : , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radiosity (computer Graphics)
In 3D computer graphics, radiosity is an application of the finite element method to solving the rendering equation for scenes with surfaces that reflect light diffusely. Unlike rendering methods that use Monte Carlo algorithms (such as path tracing), which handle all types of light paths, typical radiosity only account for paths (represented by the code "LD*E") which leave a light source and are reflected diffusely some number of times (possibly zero) before hitting the eye. Radiosity is a global illumination algorithm in the sense that the illumination arriving on a surface comes not just directly from the light sources, but also from other surfaces reflecting light. Radiosity is viewpoint independent, which increases the calculations involved, but makes them useful for all viewpoints. Radiosity methods were first developed in about 1950 in the engineering field of heat transfer. They were later refined specifically for the problem of rendering computer graphics in 19 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiple Scattering Theory
Multiple scattering theory (MST) is the mathematical formalism that is used to describe the propagation of a wave through a collection of scatterers. Examples are acoustical waves traveling through porous media, light scattering from water droplets in a cloud, or x-rays scattering from a crystal. A more recent application is to the propagation of quantum matter waves like electrons or neutrons through a solid. As pointed out by Jan Korringa, the origin of this theory can be traced back to an 1892 paper by Lord Rayleigh. An important mathematical formulation of the theory was made by Paul Peter Ewald. Korringa and Ewald acknowledged the influence on their work of the 1903 doctoral dissertation of Nikolai Kasterin, portions of which were published in German in the Proceedings of the Royal Academy of Sciences in Amsterdam under the sponsorship of Heike Kamerlingh Onnes. The MST formalism is widely used for electronic structure calculations as well as diffraction theory, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
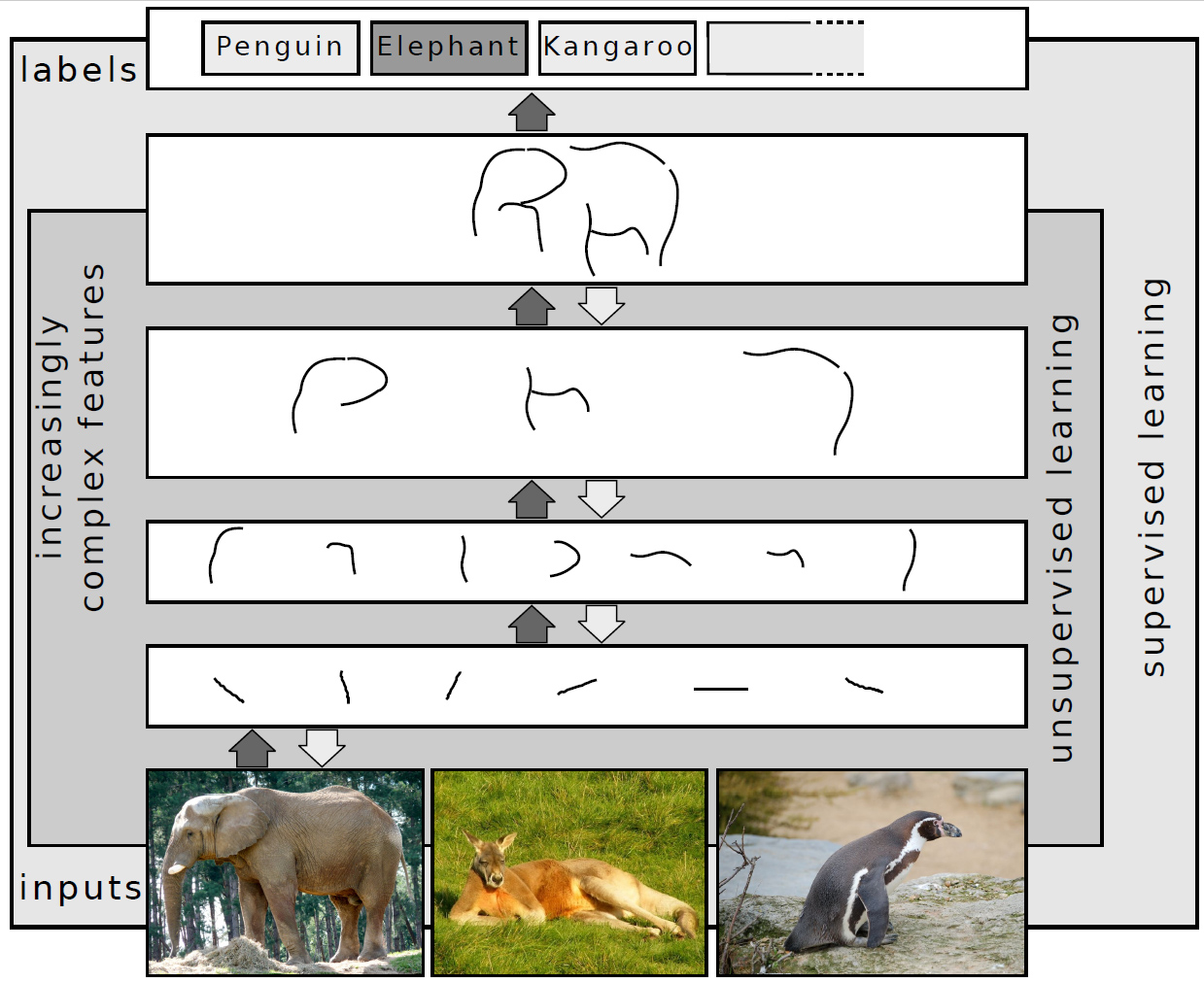
Deep Neural Networks
Deep learning is a subset of machine learning that focuses on utilizing multilayered neural networks to perform tasks such as classification, regression, and representation learning. The field takes inspiration from biological neuroscience and is centered around stacking artificial neurons into layers and "training" them to process data. The adjective "deep" refers to the use of multiple layers (ranging from three to several hundred or thousands) in the network. Methods used can be either supervised, semi-supervised or unsupervised. Some common deep learning network architectures include fully connected networks, deep belief networks, recurrent neural networks, convolutional neural networks, generative adversarial networks, transformers, and neural radiance fields. These architectures have been applied to fields including computer vision, speech recognition, natural language processing, machine translation, bioinformatics, drug design, medical image analysis, climat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximate Bayesian Computation
Approximate Bayesian computation (ABC) constitutes a class of computational methods rooted in Bayesian statistics that can be used to estimate the posterior distributions of model parameters. In all model-based statistical inference, the likelihood function is of central importance, since it expresses the probability of the observed data under a particular statistical model, and thus quantifies the support data lend to particular values of parameters and to choices among different models. For simple models, an analytical formula for the likelihood function can typically be derived. However, for more complex models, an analytical formula might be elusive or the likelihood function might be computationally very costly to evaluate. ABC methods bypass the evaluation of the likelihood function. In this way, ABC methods widen the realm of models for which statistical inference can be considered. ABC methods are mathematically well-founded, but they inevitably make assumptions and app ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Method Of Moments (statistics)
In statistics, the method of moments is a method of estimation of population parameters. The same principle is used to derive higher moments like skewness and kurtosis. It starts by expressing the population moments (i.e., the expected values of powers of the random variable under consideration) as functions of the parameters of interest. Those expressions are then set equal to the sample moments. The number of such equations is the same as the number of parameters to be estimated. Those equations are then solved for the parameters of interest. The solutions are estimates of those parameters. The method of moments was introduced by Pafnuty Chebyshev in 1887 in the proof of the central limit theorem. The idea of matching empirical moments of a distribution to the population moments dates back at least to Karl Pearson. Method Suppose that the parameter \theta = (\theta_1, \theta_2, \dots, \theta_k) characterizes the distribution f_W(w; \theta) of the random variable W. Supp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiple Scattering
In physics, scattering is a wide range of physical processes where moving particles or radiation of some form, such as light or sound, are forced to deviate from a straight trajectory by localized non-uniformities (including particles and radiation) in the medium through which they pass. In conventional use, this also includes deviation of reflected radiation from the angle predicted by the law of reflection. Reflections of radiation that undergo scattering are often called ''diffuse reflections'' and unscattered reflections are called ''specular'' (mirror-like) reflections. Originally, the term was confined to light scattering (going back at least as far as Isaac Newton in the 17th century). As more "ray"-like phenomena were discovered, the idea of scattering was extended to them, so that William Herschel could refer to the scattering of "heat rays" (not then recognized as electromagnetic in nature) in 1800. John Tyndall, a pioneer in light scattering research, noted the connecti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Radius
''Spectral'' is a 2016 Hungarian-American military science fiction action film co-written and directed by Nic Mathieu. Written with Ian Fried (screenwriter), Ian Fried & George Nolfi, the film stars James Badge Dale as DARPA research scientist Mark Clyne, with Max Martini, Emily Mortimer, Clayne Crawford, and Bruce Greenwood in supporting roles. The film is set in a civil war-ridden Moldova as invisible entities slaughter any living being caught in their path. The film was released worldwide on December 9, 2016 on Netflix. On February 1, 2017, Netflix released a prequel graphic novel of the film called ''Spectral: Ghosts of War'' which was made available digitally through the website ComiXology. Plot DARPA researcher Mark Clyne is sent to a United States, US United States Armed Forces, military Air base, airbase on the outskirts of Chișinău, to consult his created line of hyperspectral imaging goggles issued to United States Army, US Army United States Army Special Forces, S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Modelling
A mathematical model is an abstract description of a concrete system using mathematical concepts and language. The process of developing a mathematical model is termed ''mathematical modeling''. Mathematical models are used in applied mathematics and in the natural sciences (such as physics, biology, earth science, chemistry) and engineering disciplines (such as computer science, electrical engineering), as well as in non-physical systems such as the social sciences (such as economics, psychology, sociology, political science). It can also be taught as a subject in its own right. The use of mathematical models to solve problems in business or military operations is a large part of the field of operations research. Mathematical models are also used in music, linguistics, and philosophy (for example, intensively in analytic philosophy). A model may help to explain a system and to study the effects of different components, and to make predictions about behavior. Elements of a math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Series
In mathematics, a geometric series is a series (mathematics), series summing the terms of an infinite geometric sequence, in which the ratio of consecutive terms is constant. For example, 1/2 + 1/4 + 1/8 + 1/16 + ⋯, the series \tfrac12 + \tfrac14 + \tfrac18 + \cdots is a geometric series with common ratio , which converges to the sum of . Each term in a geometric series is the geometric mean of the term before it and the term after it, in the same way that each term of an arithmetic series is the arithmetic mean of its neighbors. While Ancient Greek philosophy, Greek philosopher Zeno's paradoxes about time and motion (5th century BCE) have been interpreted as involving geometric series, such series were formally studied and applied a century or two later by Greek mathematics, Greek mathematicians, for example used by Archimedes to Quadrature of the Parabola, calculate the area inside a parabola (3rd century BCE). Today, geometric series are used in mathematical finance, calculati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |