 |
Point Spread Function
The point spread function (PSF) describes the response of a focused optical imaging system to a point source or point object. A more general term for the PSF is the system's impulse response; the PSF is the impulse response or impulse response function (IRF) of a focused optical imaging system. The PSF in many contexts can be thought of as the shapeless blob in an image that should represent a single point object. We can consider this as a spatial impulse response function. In functional terms, it is the spatial domain version (i.e., the inverse Fourier transform) of the Optical transfer function, optical transfer function (OTF) of an imaging system. It is a useful concept in Fourier optics, astronomy, astronomical imaging, medical imaging, electron microscope, electron microscopy and other imaging techniques such as dimension, 3D microscopy (like in confocal laser scanning microscopy) and fluorescence microscopy. The degree of spreading (blurring) in the image of a point ob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Convolution Illustrated Eng
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The term ''convolution'' refers to both the resulting function and to the process of computing it. The integral is evaluated for all values of shift, producing the convolution function. The choice of which function is reflected and shifted before the integral does not change the integral result (see #Properties, commutativity). Graphically, it expresses how the 'shape' of one function is modified by the other. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution f*g differs from cross-correlation f \star g only in that either f(x) or g(x) is reflected about the y-axis in convolution; thus i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Telescopes
A telescope is a device used to observe distant objects by their emission, Absorption (electromagnetic radiation), absorption, or Reflection (physics), reflection of electromagnetic radiation. Originally, it was an optical instrument using lenses, curved mirrors, or a combination of both to observe distant objects – an optical telescope. Nowadays, the word "telescope" is defined as a wide range of instruments capable of detecting different regions of the electromagnetic spectrum, and in some cases other types of detectors. The first known practical telescopes were refracting telescopes with glass lenses and were invented in the Netherlands at the beginning of the 17th century. They were used for both terrestrial applications and astronomy. The reflecting telescope, which uses mirrors to collect and focus light, was invented within a few decades of the first refracting telescope. In the 20th century, many new types of telescopes were invented, including radio telescopes in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
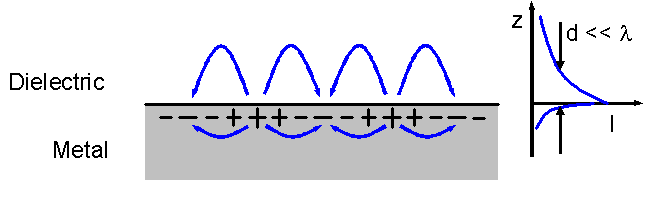 |
Evanescent Wave
In electromagnetics, an evanescent field, or evanescent wave, is an oscillating electric and/or magnetic field that does not propagate as an electromagnetic wave but whose energy is spatially concentrated in the vicinity of the source (oscillating charges and currents). Even when there is a propagating electromagnetic wave produced (e.g., by a transmitting antenna), one can still identify as an evanescent field the component of the electric or magnetic field that cannot be attributed to the propagating wave observed at a distance of many wavelengths (such as the far field of a transmitting antenna). A hallmark of an evanescent field is that there is no net energy flow in that region. Since the net flow of electromagnetic energy is given by the average Poynting vector, this means that the Poynting vector in these regions, as averaged over a complete oscillation cycle, is zero. Use of the term In many cases one cannot simply say that a field is or is not "evanescent" – hav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Huygens–Fresnel Principle
The Huygens–Fresnel principle (named after Netherlands, Dutch physicist Christiaan Huygens and France, French physicist Augustin-Jean Fresnel) states that every point on a wavefront is itself the source of spherical wavelets, and the secondary wavelets emanating from different points mutually Wave interference, interfere. The sum of these spherical wavelets forms a new wavefront. As such, the Huygens-Fresnel principle is a method of analysis applied to problems of luminous wave propagation both in the Far-field diffraction pattern, far-field limit and in near-field diffraction as well as Reflection (physics), reflection. History In 1678, Huygens proposed that every point reached by a luminous disturbance becomes a source of a spherical wave. The sum of these secondary waves determines the form of the wave at any subsequent time; the overall procedure is referred to as Huygens' construction. He assumed that the secondary waves travelled only in the "forward" direction, and it is n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Continuous Function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Magnification
Magnification is the process of enlarging the apparent size, not physical size, of something. This enlargement is quantified by a size ratio called optical magnification. When this number is less than one, it refers to a reduction in size, sometimes called ''de-magnification''. Typically, magnification is related to scaling up visuals or images to be able to see more detail, increasing resolution, using microscope, printing techniques, or digital processing. In all cases, the magnification of the image does not change the perspective of the image. Examples of magnification Some optical instruments provide visual aid by magnifying small or distant subjects. * A magnifying glass, which uses a positive (convex) lens to make things look bigger by allowing the user to hold them closer to their eye. * A telescope, which uses its large objective lens or primary mirror to create an image of a distant object and then allows the user to examine the image closely with a smaller ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Gaussian Beam
In optics, a Gaussian beam is an idealized beam of electromagnetic radiation whose amplitude envelope in the transverse plane is given by a Gaussian function; this also implies a Gaussian intensity (irradiance) profile. This fundamental (or TEM00) transverse Gaussian mode describes the intended output of many lasers, as such a beam diverges less and can be focused better than any other. When a Gaussian beam is refocused by an ideal lens, a new Gaussian beam is produced. The electric and magnetic field amplitude profiles along a circular Gaussian beam of a given wavelength and polarization are determined by two parameters: the waist , which is a measure of the width of the beam at its narrowest point, and the position relative to the waist.Svelto, pp. 153–5. Since the Gaussian function is infinite in extent, perfect Gaussian beams do not exist in nature, and the edges of any such beam would be cut off by any finite lens or mirror. However, the Gaussian is a useful appro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Deconvolution
In mathematics, deconvolution is the inverse of convolution. Both operations are used in signal processing and image processing. For example, it may be possible to recover the original signal after a filter (convolution) by using a deconvolution method with a certain degree of accuracy. Due to the measurement error of the recorded signal or image, it can be demonstrated that the worse the signal-to-noise ratio (SNR), the worse the reversing of a filter will be; hence, inverting a filter is not always a good solution as the error amplifies. Deconvolution offers a solution to this problem. The foundations for deconvolution and time-series analysis were largely laid by Norbert Wiener of the Massachusetts Institute of Technology in his book ''Extrapolation, Interpolation, and Smoothing of Stationary Time Series'' (1949). The book was based on work Wiener had done during World War II but that had been classified at the time. Some of the early attempts to apply these theories were in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Microscope Image Processing
Microscope image processing is a broad term that covers the use of digital image processing techniques to process, analyze and present images obtained from a microscope. Such processing is now commonplace in a number of diverse fields such as medicine, biological research, cancer research, drug testing, metallurgy, etc. A number of manufacturers of microscopes now specifically design in features that allow the microscopes to interface to an image processing system. Image acquisition Until the early 1990s, most image acquisition in video microscopy applications was typically done with an analog video camera, often simply closed circuit TV cameras. While this required the use of a frame grabber to digitize the images, video cameras provided images at full video frame rate (25-30 frames per second) allowing live video recording and processing. While the advent of solid state detectors yielded several advantages, the real-time video camera was actually superior in many respects. To ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
PSF Deconvolution V
PSF is an abbreviation that may refer to: Organisations Political parties * French Social Party ''(Parti Social Français)'' (1936–1940), a right-wing nationalist party * French Socialist Party ''(Parti Socialiste Français)'', active since 1969 * Palestinian Popular Struggle Front * Peoples Students Federation, the youth wing of the Pakistan Peoples Party * Provisional Sinn Féin, Ireland * Socialist Party without Borders ''(Parti Socialiste sans Frontières)'', a leftist party in Chad Law enforcement * Public Security Forces the principal law-enforcement arm of the Bahraini Ministry of Interior * Puntland Security Force, Somalia Business and companies * P.S.F. Records, a record label * Pennsylvania Shakespeare Festival, a professional theatre company * Professional service firm, a company offering consulting, legal, or other services * Premium Standard Farms, Inc, a pork producer * Pressed Steel Fisher, a supplier of British car parts Other organisations * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Green's Functions
In mathematics, a Green's function (or Green function) is the impulse response of an inhomogeneous linear differential operator defined on a domain with specified initial conditions or boundary conditions. This means that if L is a linear differential operator, then * the Green's function G is the solution of the equation where \delta is Dirac's delta function; * the solution of the initial-value problem L y = f is the convolution Through the superposition principle, given a linear ordinary differential equation (ODE), one can first solve for each , and realizing that, since the source is a sum of delta functions, the solution is a sum of Green's functions as well, by linearity of . Green's functions are named after the British mathematician George Green, who first developed the concept in the 1820s. In the modern study of linear partial differential equations, Green's functions are studied largely from the point of view of fundamental solutions instead. Under many- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |