|
Convolution Illustrated Eng
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The term ''convolution'' refers to both the resulting function and to the process of computing it. The integral is evaluated for all values of shift, producing the convolution function. The choice of which function is reflected and shifted before the integral does not change the integral result (see #Properties, commutativity). Graphically, it expresses how the 'shape' of one function is modified by the other. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution f*g differs from cross-correlation f \star g only in that either f(x) or g(x) is reflected about the y-axis in convolution; thus i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Comparison Convolution Correlation
Comparison or comparing is the act of evaluating two or more things by determining the relevant, comparable characteristics of each thing, and then determining which characteristics of each are similar to the other, which are different, and to what degree. Where characteristics are different, the differences may then be evaluated to determine which thing is best suited for a particular purpose. The description of similarities and differences found between the two things is also called a comparison. Comparison can take many distinct forms, varying by field: To compare things, they must have characteristics that are similar enough in relevant ways to merit comparison. If two things are too different to compare in a useful way, an attempt to compare them is colloquially referred to in English as "comparing apples and oranges." Comparison is widely used in society, in science and the arts. General usage Comparison is a natural activity, which even animals engage in when decidi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
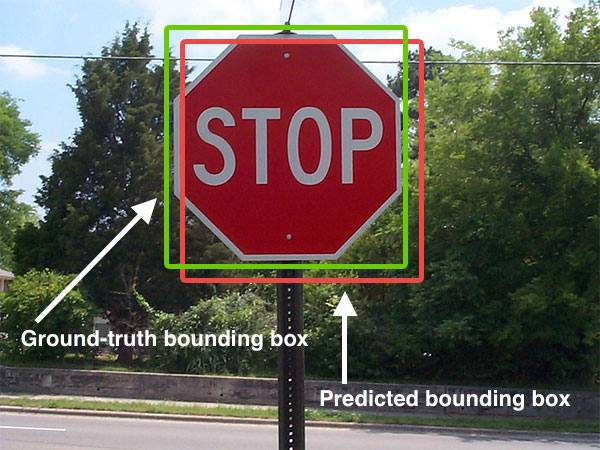
Image Processing
An image or picture is a visual representation. An image can be two-dimensional, such as a drawing, painting, or photograph, or three-dimensional, such as a carving or sculpture. Images may be displayed through other media, including a projection on a surface, activation of electronic signals, or digital displays; they can also be reproduced through mechanical means, such as photography, printmaking, or photocopying. Images can also be animated through digital or physical processes. In the context of signal processing, an image is a distributed amplitude of color(s). In optics, the term ''image'' (or ''optical image'') refers specifically to the reproduction of an object formed by light waves coming from the object. A ''volatile image'' exists or is perceived only for a short period. This may be a reflection of an object by a mirror, a projection of a camera obscura, or a scene displayed on a cathode-ray tube. A ''fixed image'', also called a hard copy, is one that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative integers. The set (mathematics), set of all integers is often denoted by the boldface or blackboard bold The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the set of natural numbers, the set of integers \mathbb is Countable set, countably infinite. An integer may be regarded as a real number that can be written without a fraction, fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , 5/4, and Square root of 2, are not. The integers form the smallest Group (mathematics), group and the smallest ring (mathematics), ring containing the natural numbers. In algebraic number theory, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Convolution
Circular convolution, also known as cyclic convolution, is a special case of periodic convolution, which is the convolution of two periodic functions that have the same period. Periodic convolution arises, for example, in the context of the discrete-time Fourier transform (DTFT). In particular, the DTFT of the product of two discrete sequences is the periodic convolution of the DTFTs of the individual sequences. And each DTFT is a periodic summation of a continuous Fourier transform function (see ). Although DTFTs are usually continuous functions of frequency, the concepts of periodic and circular convolution are also directly applicable to discrete sequences of data. In that context, circular convolution plays an important role in maximizing the efficiency of a certain kind of common filtering operation. Definitions The ''periodic convolution'' of two T-periodic functions, h_(t) and x_(t) can be defined as: :\int_^ h_(\tau)\cdot x_(t - \tau)\,d\tau, where t_o is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete-time Fourier Transform
In mathematics, the discrete-time Fourier transform (DTFT) is a form of Fourier analysis that is applicable to a sequence of discrete values. The DTFT is often used to analyze samples of a continuous function. The term ''discrete-time'' refers to the fact that the transform operates on discrete data, often samples whose interval has units of time. From uniformly spaced samples it produces a function of frequency that is a periodic summation of the continuous Fourier transform of the original continuous function. In simpler terms, when you take the DTFT of regularly-spaced samples of a continuous signal, you get repeating (and possibly overlapping) copies of the signal's frequency spectrum, spaced at intervals corresponding to the sampling frequency. Under certain theoretical conditions, described by the sampling theorem, the original continuous function can be recovered perfectly from the DTFT and thus from the original discrete samples. The DTFT itself is a continuous functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Function
A periodic function, also called a periodic waveform (or simply periodic wave), is a function that repeats its values at regular intervals or periods. The repeatable part of the function or waveform is called a ''cycle''. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to describe oscillations, waves, and other phenomena that exhibit periodicity. Any function that is not periodic is called ''aperiodic''. Definition A function is said to be periodic if, for some nonzero constant , it is the case that :f(x+P) = f(x) for all values of in the domain. A nonzero constant for which this is the case is called a period of the function. If there exists a least positive constant with this property, it is called the fundamental period (also primitive period, basic period, or prime period.) Often, "the" period of a function is used to mean its fundamental period. A funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Structure
In mathematics, an algebraic structure or algebraic system consists of a nonempty set ''A'' (called the underlying set, carrier set or domain), a collection of operations on ''A'' (typically binary operations such as addition and multiplication), and a finite set of identities (known as ''axioms'') that these operations must satisfy. An algebraic structure may be based on other algebraic structures with operations and axioms involving several structures. For instance, a vector space involves a second structure called a field, and an operation called ''scalar multiplication'' between elements of the field (called '' scalars''), and elements of the vector space (called '' vectors''). Abstract algebra is the name that is commonly given to the study of algebraic structures. The general theory of algebraic structures has been formalized in universal algebra. Category theory is another formalization that includes also other mathematical structures and functions between structu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group (mathematics)
In mathematics, a group is a Set (mathematics), set with an Binary operation, operation that combines any two elements of the set to produce a third element within the same set and the following conditions must hold: the operation is Associative property, associative, it has an identity element, and every element of the set has an inverse element. For example, the integers with the addition, addition operation form a group. The concept of a group was elaborated for handling, in a unified way, many mathematical structures such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics. In geometry, groups arise naturally in the study of symmetries and geometric transformations: The symmetries of an object form a group, called the symmetry group of the object, and the transformations of a given type form a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces'' of any positive integer dimension ''n'', which are called Euclidean ''n''-spaces when one wants to specify their dimension. For ''n'' equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of '' proving'' all properties of the space as theorems, by starting from a few fundamental properties, called '' postulates'', which either were considered as evid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Vision
Computer vision tasks include methods for image sensor, acquiring, Image processing, processing, Image analysis, analyzing, and understanding digital images, and extraction of high-dimensional data from the real world in order to produce numerical or symbolic information, e.g. in the form of decisions. "Understanding" in this context signifies the transformation of visual images (the input to the retina) into descriptions of the world that make sense to thought processes and can elicit appropriate action. This image understanding can be seen as the disentangling of symbolic information from image data using models constructed with the aid of geometry, physics, statistics, and learning theory. The scientific discipline of computer vision is concerned with the theory behind artificial systems that extract information from images. Image data can take many forms, such as video sequences, views from multiple cameras, multi-dimensional data from a 3D scanning, 3D scanner, 3D point clouds ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |