|
Orthogonality
In mathematics, orthogonality is the generalization of the geometric notion of '' perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendicular'' is more specifically used for lines and planes that intersect to form a right angle, whereas ''orthogonal'' is used in generalizations, such as ''orthogonal vectors'' or ''orthogonal curves''. ''Orthogonality'' is also used with various meanings that are often weakly related or not related at all with the mathematical meanings. Etymology The word comes from the Ancient Greek ('), meaning "upright", and ('), meaning "angle". The Ancient Greek (') and Classical Latin ' originally denoted a rectangle. Later, they came to mean a right triangle. In the 12th century, the post-classical Latin word ''orthogonalis'' came to mean a right angle or something related to a right angle. Mathematics Physics Optics In optics, polarization states are said to be ort ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonality (mathematics)
In mathematics, orthogonality is the generalization of the geometric notion of ''perpendicularity'' to linear algebra of bilinear forms. Two elements and of a vector space with bilinear form B are orthogonal when B(\mathbf,\mathbf)= 0. Depending on the bilinear form, the vector space may contain null vectors, non-zero self-orthogonal vectors, in which case perpendicularity is replaced with hyperbolic orthogonality. In the case of function spaces, families of functions are used to form an orthogonal basis (linear algebra), basis, such as in the contexts of orthogonal polynomials, orthogonal functions, and combinatorics. Definitions * In geometry, two Euclidean vectors are orthogonal if they are perpendicular, ''i.e.'' they form a right angle. * Two vector space, vectors and in an inner product space V are ''orthogonal'' if their inner product \langle \mathbf, \mathbf \rangle is zero. This relationship is denoted \mathbf \perp \mathbf. * A set of vectors in an inner produ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal Vectors
In mathematics, an inner product space (or, rarely, a Hausdorff space, Hausdorff pre-Hilbert space) is a real vector space or a complex vector space with an operation (mathematics), operation called an inner product. The inner product of two vectors in the space is a Scalar (mathematics), scalar, often denoted with angle brackets such as in \langle a, b \rangle. Inner products allow formal definitions of intuitive geometric notions, such as lengths, angles, and orthogonality (zero inner product) of vectors. Inner product spaces generalize Euclidean vector spaces, in which the inner product is the dot product or ''scalar product'' of Cartesian coordinates. Inner product spaces of infinite Dimension (vector space), dimension are widely used in functional analysis. Inner product spaces over the Field (mathematics), field of complex numbers are sometimes referred to as unitary spaces. The first usage of the concept of a vector space with an inner product is due to Giuseppe Peano, in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
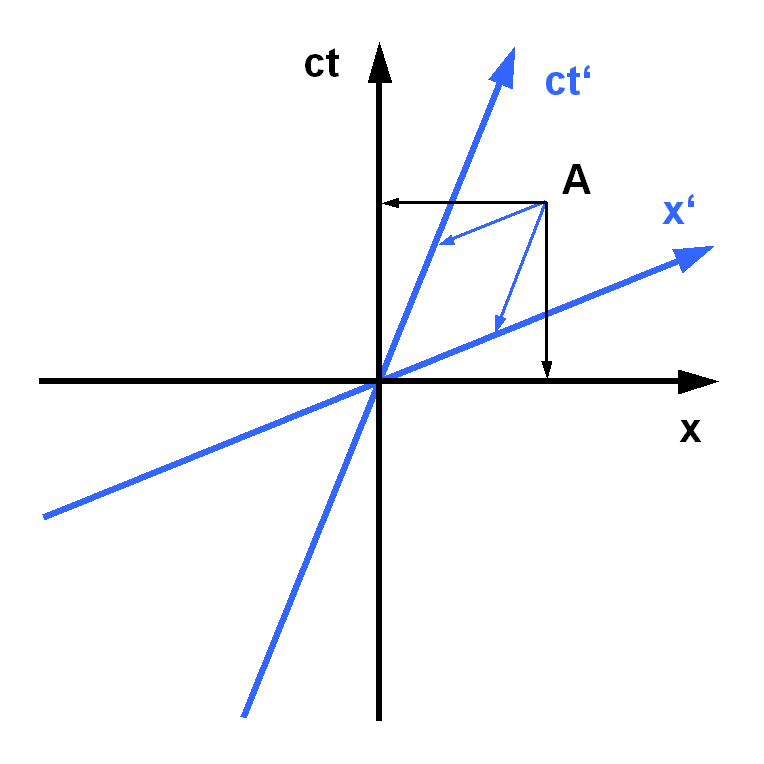
Hyperbolic Orthogonality
In geometry, the relation of hyperbolic orthogonality between two lines separated by the asymptotes of a hyperbola is a concept used in special relativity to define simultaneous events. Two events will be simultaneous when they are on a line hyperbolically orthogonal to a particular timeline. This dependence on a certain timeline is determined by velocity, and is the basis for the relativity of simultaneity. Furthermore, keeping time and space axes hyperbolically orthogonal, as in Minkowski space, gives a constant result when measurements are taken of the speed of light. Geometry Two lines are hyperbolic orthogonal when they are reflections of each other over the asymptote of a given hyperbola. Two particular hyperbolas are frequently used in the plane: The relation of hyperbolic orthogonality actually applies to classes of parallel lines in the plane, where any particular line can represent the class. Thus, for a given hyperbola and asymptote ''A'', a pair of lines (''a'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relativity Of Simultaneity
In physics, the relativity of simultaneity is the concept that ''distant simultaneity'' – whether two spatially separated events occur at the same time – is not absolute, but depends on the observer's reference frame. This possibility was raised by mathematician Henri Poincaré in 1900, and thereafter became a central idea in the special theory of relativity. Description According to the special theory of relativity introduced by Albert Einstein, it is impossible to say in an ''absolute'' sense that two distinct events occur at the same time if those events are separated in space. If one reference frame assigns precisely the same time to two events that are at different points in space, a reference frame that is moving relative to the first will generally assign different times to the two events (the only exception being when motion is exactly perpendicular to the line connecting the locations of both events). For example, a car crash in London and another in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Special Relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory of the relationship between Spacetime, space and time. In Albert Einstein's 1905 paper, Annus Mirabilis papers#Special relativity, "On the Electrodynamics of Moving Bodies", the theory is presented as being based on just Postulates of special relativity, two postulates: # The laws of physics are Invariant (physics), invariant (identical) in all Inertial frame of reference, inertial frames of reference (that is, Frame of reference, frames of reference with no acceleration). This is known as the principle of relativity. # The speed of light in vacuum is the same for all observers, regardless of the motion of light source or observer. This is known as the principle of light constancy, or the principle of light speed invariance. The first postulate was first formulated by Galileo Galilei (see ''Galilean invariance''). Background Special relativity builds upon important physics ide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polarization (waves)
, or , is a property of transverse waves which specifies the geometrical orientation of the oscillations. In a transverse wave, the direction of the oscillation is perpendicular to the direction of motion of the wave. One example of a polarized transverse wave is vibrations traveling along a taut string, for example, in a musical instrument like a guitar string. Depending on how the string is plucked, the vibrations can be in a vertical direction, horizontal direction, or at any angle perpendicular to the string. In contrast, in longitudinal waves, such as sound waves in a liquid or gas, the displacement of the particles in the oscillation is always in the direction of propagation, so these waves do not exhibit polarization. Transverse waves that exhibit polarization include electromagnetic waves such as light and radio waves, gravitational waves, and transverse sound waves ( shear waves) in solids. An electromagnetic wave such as light consists of a coupled oscillating el ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Triangle
A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle ( turn or 90 degrees). The side opposite to the right angle is called the '' hypotenuse'' (side c in the figure). The sides adjacent to the right angle are called ''legs'' (or ''catheti'', singular: '' cathetus''). Side a may be identified as the side ''adjacent'' to angle B and ''opposite'' (or ''opposed to'') angle A, while side b is the side adjacent to angle A and opposite angle B. Every right triangle is half of a rectangle which has been divided along its diagonal. When the rectangle is a square, its right-triangular half is isosceles, with two congruent sides and two congruent angles. When the rectangle is not a square, its right-triangular half is scalene. Every triangle whose base is the diameter of a circle and whose apex lies on the circle is a right triangle, with the right angle at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perpendicularity
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', ⟂. Perpendicular intersections can happen between two lines (or two line segments), between a line and a plane, and between two planes. ''Perpendicular'' is also used as a noun: a perpendicular is a line which is perpendicular to a given line or plane. Perpendicularity is one particular instance of the more general mathematical concept of ''orthogonality''; perpendicularity is the orthogonality of classical geometric objects. Thus, in advanced mathematics, the word "perpendicular" is sometimes used to describe much more complicated geometric orthogonality conditions, such as that between a surface and its '' normal vector''. A line is said to be perpendicular to another line if the two lines intersect at a right angle. Explicitly, a fir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Angle
In geometry and trigonometry, a right angle is an angle of exactly 90 Degree (angle), degrees or radians corresponding to a quarter turn (geometry), turn. If a Line (mathematics)#Ray, ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles. The term is a calque of Latin ''angulus rectus''; here ''rectus'' means "upright", referring to the vertical perpendicular to a horizontal base line. Closely related and important geometrical concepts are perpendicular lines, meaning lines that form right angles at their point of intersection, and orthogonality, which is the property of forming right angles, usually applied to Euclidean vector, vectors. The presence of a right angle in a triangle is the defining factor for right triangles, making the right angle basic to trigonometry. Etymology The meaning of ''right'' in ''right angle'' possibly refers to the Classical Latin, Latin adjective ''rectus'' 'erect, straight, upright, perp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Piet Mondrian
Pieter Cornelis Mondriaan (; 7 March 1872 – 1 February 1944), known after 1911 as Piet Mondrian (, , ), was a Dutch Painting, painter and Theory of art, art theoretician who is regarded as one of the greatest artists of the 20th century. He was one of the pioneers of 20th-century abstract art, as he changed his artistic direction from figurative painting to an increasingly abstract style, until he reached a point where his artistic vocabulary was reduced to simple geometric elements. Mondrian's art was highly utopian and was concerned with a search for universal values and aesthetics. He proclaimed in 1914: "Art is higher than reality and has no direct relation to reality. To approach the Spirituality, spiritual in art, one will make as little use as possible of reality, because reality is opposed to the spiritual. We find ourselves in the presence of an abstract art. Art should be above reality, otherwise it would have no value for man." He was a contributor to the ''De Stij ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vanishing Point
A vanishing point is a point (geometry), point on the projection plane, image plane of a graphical perspective, perspective rendering where the two-dimensional perspective projections of parallel (geometry), parallel lines in three-dimensional space appear to converge. When the set of parallel lines is perpendicular to a picture plane, the construction is known as one-point perspective, and their vanishing point corresponds to the station point, oculus, or "eye point", from which the image should be viewed for correct perspective geometry.Kirsti Andersen (2007) ''Geometry of an Art'', p. xxx, Springer, Traditional linear drawings use objects with one to three sets of parallels, defining one to three vanishing points. Italian Renaissance humanism, humanist polymath and architect Leon Battista Alberti first introduced the concept in his treatise on perspective in art, ''De pictura'', written in 1435. Straight Track geometry, railroad tracks are a familiar modern example. Vector ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perspective (graphical)
Linear or point-projection perspective () is one of two types of graphical projection perspective in the graphic arts; the other is parallel projection. Linear perspective is an approximate representation, generally on a flat surface, of an image as it is seen by the eye. Perspective drawing is useful for representing a three-dimensional scene in a two-dimensional medium, like paper. It is based on the optical fact that for a person an object looks N times (linearly) smaller if it has been moved N times further from the eye than the original distance was. The most characteristic features of linear perspective are that objects appear smaller as their distance from the observer increases, and that they are subject to , meaning that an object's dimensions parallel to the line of sight appear shorter than its dimensions perpendicular to the line of sight. All objects will recede to points in the distance, usually along the horizon line, but also above and below the horiz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |