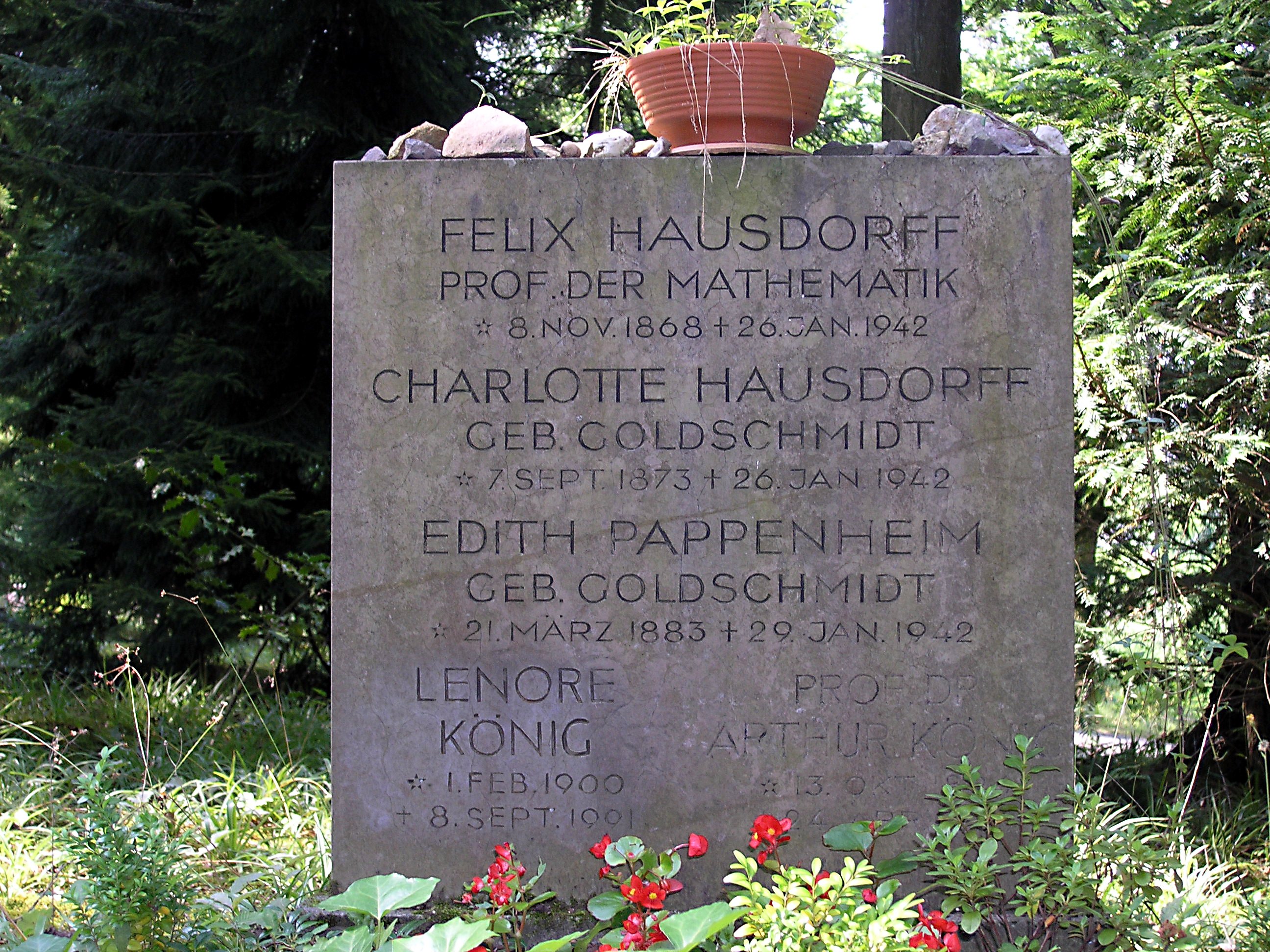|
Ordered Pair
In mathematics, an ordered pair, denoted (''a'', ''b''), is a pair of objects in which their order is significant. The ordered pair (''a'', ''b'') is different from the ordered pair (''b'', ''a''), unless ''a'' = ''b''. In contrast, the '' unordered pair'', denoted , always equals the unordered pair . Ordered pairs are also called 2-tuples, or sequences (sometimes, lists in a computer science context) of length 2. Ordered pairs of scalars are sometimes called 2-dimensional vectors. (Technically, this is an abuse of terminology since an ordered pair need not be an element of a vector space.) The entries of an ordered pair can be other ordered pairs, enabling the recursive definition of ordered ''n''-tuples (ordered lists of ''n'' objects). For example, the ordered triple (''a'',''b'',''c'') can be defined as (''a'', (''b'',''c'')), i.e., as one pair nested in another. In the ordered pair (''a'', ''b''), the object ''a'' is called the ''first entry'', and the object ''b'' the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Product
In mathematics, specifically set theory, the Cartesian product of two sets and , denoted , is the set of all ordered pairs where is an element of and is an element of . In terms of set-builder notation, that is A\times B = \. A table can be created by taking the Cartesian product of a set of rows and a set of columns. If the Cartesian product is taken, the cells of the table contain ordered pairs of the form . One can similarly define the Cartesian product of sets, also known as an -fold Cartesian product, which can be represented by an -dimensional array, where each element is an -tuple. An ordered pair is a 2-tuple or couple. More generally still, one can define the Cartesian product of an indexed family of sets. The Cartesian product is named after René Descartes, whose formulation of analytic geometry gave rise to the concept, which is further generalized in terms of direct product. Set-theoretic definition A rigorous definition of the Cartesian product re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipse In Coordinate System With Semi-axes Labelled
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity (mathematics), eccentricity e, a number ranging from e = 0 (the Limiting case (mathematics), limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but for Perimeter of an ellipse, its perimeter (also known as circumference), Integral, integration is required to obtain an exact solution. The largest and smallest diameters of an ellipse, also known as its width and height, are typically denoted and . An ellipse has four extreme points: two ''Vertex (geometry), vertices'' at the endpoints of the major axis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number Line
A number line is a graphical representation of a straight line that serves as spatial representation of numbers, usually graduated like a ruler with a particular origin point representing the number zero and evenly spaced marks in either direction representing integers, imagined to extend infinitely. The association between numbers and points on the line links arithmetical operations on numbers to geometric relations between points, and provides a conceptual framework for learning mathematics. In elementary mathematics, the number line is initially used to teach addition and subtraction of integers, especially involving negative numbers. As students progress, more kinds of numbers can be placed on the line, including fractions, decimal fractions, square roots, and transcendental numbers such as the circle constant : Every point of the number line corresponds to a unique real number, and every real number to a unique point. Using a number line, numerical concepts can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamenta Mathematicae
''Fundamenta Mathematicae'' is a peer-reviewed scientific journal of mathematics with a special focus on the foundations of mathematics, concentrating on set theory, mathematical logic, topology and its interactions with algebra, and dynamical systems. The first specialized journal in the field of mathematics, originally it covered only topology, set theory, and foundations of mathematics..... It is published by the Mathematics Institute of the Polish Academy of Sciences. History The journal was conceived by Zygmunt Janiszewski as a means to foster mathematical research in Poland.According to and to the introduction to the 100th volume of the journal (1978, pp=1–2). These two sources cite an article written by Janiszewski himself in 1918 and titled "''On the needs of Mathematics in Poland''". Janiszewski posited that, to achieve its goal, the journal should not compel Polish mathematicians to submit articles written exclusively in Polish, and should be devoted only to a sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kazimierz Kuratowski
Kazimierz Kuratowski (; 2 February 1896 – 18 June 1980) was a Polish mathematician and logician. He was one of the leading representatives of the Warsaw School of Mathematics. He worked as a professor at the University of Warsaw and at the Mathematical Institute of the Polish Academy of Sciences (IM PAN). Between 1946 and 1953, he served as President of the Polish Mathematical Society. He is primarily known for his contributions to set theory, topology, measure theory and graph theory. Some of the notable mathematical concepts bearing Kuratowski's name include Kuratowski's theorem, Kuratowski closure axioms, Kuratowski-Zorn lemma and Kuratowski's intersection theorem. Life and career Early life Kazimierz Kuratowski was born in Warsaw, (then part of Congress Poland controlled by the Russian Empire), on 2 February 1896. He was a son of Marek Kuratow, a barrister, and Róża Karzewska. He completed a Warsaw secondary school, which was named after general Paweł Chrzanowski. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Felix Hausdorff
Felix Hausdorff ( , ; November 8, 1868 – January 26, 1942) was a German mathematician, pseudonym Paul Mongré (''à mogré' (Fr.) = "according to my taste"), who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, and functional analysis. Hausdorff was Jewish, and life became difficult for him and his family after the '' Kristallnacht'' of 1938. The next year he initiated efforts to emigrate to the United States, but was unable to make arrangements to receive a research fellowship. On 26 January 1942, Hausdorff, along with his wife and his sister-in-law, died by suicide by taking an overdose of veronal, rather than comply with German orders to move to the Endenich camp, and there suffer the likely implications, about which he held no illusions. Life Childhood and youth Hausdorff's father, the Jewish merchant Louis Hausdorff (1843–1896), moved with his young family to Leipzig in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relation (mathematics)
In mathematics, a relation denotes some kind of ''relationship'' between two mathematical object, objects in a Set (mathematics), set, which may or may not hold. As an example, "''is less than''" is a relation on the set of natural numbers; it holds, for instance, between the values and (denoted as ), and likewise between and (denoted as ), but not between the values and nor between and , that is, and both evaluate to false. As another example, "''is sister of'' is a relation on the set of all people, it holds e.g. between Marie Curie and Bronisława Dłuska, and likewise vice versa. Set members may not be in relation "to a certain degree" – either they are in relation or they are not. Formally, a relation over a set can be seen as a set of ordered pairs of members of . The relation holds between and if is a member of . For example, the relation "''is less than''" on the natural numbers is an infinite set of pairs of natural numbers that contains both and , b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principia Mathematica
The ''Principia Mathematica'' (often abbreviated ''PM'') is a three-volume work on the foundations of mathematics written by the mathematician–philosophers Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913. In 1925–1927, it appeared in a second edition with an important ''Introduction to the Second Edition'', an ''Appendix A'' that replaced ✱9 with a new ''Appendix B'' and ''Appendix C''. ''PM'' was conceived as a sequel to Russell's 1903 '' The Principles of Mathematics'', but as ''PM'' states, this became an unworkable suggestion for practical and philosophical reasons: "The present work was originally intended by us to be comprised in a second volume of ''Principles of Mathematics''... But as we advanced, it became increasingly evident that the subject is a very much larger one than we had supposed; moreover on many fundamental questions which had been left obscure and doubtful in the former work, we have now arrived at what we bel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Type Theory
In mathematics and theoretical computer science, a type theory is the formal presentation of a specific type system. Type theory is the academic study of type systems. Some type theories serve as alternatives to set theory as a foundation of mathematics. Two influential type theories that have been proposed as foundations are: * Typed λ-calculus of Alonzo Church * Intuitionistic type theory of Per Martin-Löf Most computerized proof-writing systems use a type theory for their foundation. A common one is Thierry Coquand's Calculus of Inductive Constructions. History Type theory was created to avoid paradoxes in naive set theory and formal logic, such as Russell's paradox which demonstrates that, without proper axioms, it is possible to define the set of all sets that are not members of themselves; this set both contains itself and does not contain itself. Between 1902 and 1908, Bertrand Russell proposed various solutions to this problem. By 1908, Russell arrive ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norbert Wiener
Norbert Wiener (November 26, 1894 – March 18, 1964) was an American computer scientist, mathematician, and philosopher. He became a professor of mathematics at the Massachusetts Institute of Technology ( MIT). A child prodigy, Wiener later became an early researcher in stochastic and mathematical noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems. Wiener is considered the originator of cybernetics, the science of communication as it relates to living things and machines, with implications for engineering, systems control, computer science, biology, neuroscience, philosophy, and the organization of society. His work heavily influenced computer pioneer John von Neumann, information theorist Claude Shannon, anthropologists Margaret Mead and Gregory Bateson, and others. Wiener is credited as being one of the first to theorize that all intelligent behavior was the result of feedback mechanisms, tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Word And Object
''Word and Object'', philosopher Willard Van Orman Quine's most famous work, expands on ideas in ''From a Logical Point of View'' (1953) and reformulates earlier arguments like his attack on the analytic–synthetic distinction from " Two Dogmas of Empiricism". It introduces the thought experiment of radical translation and the related concept of indeterminacy of translation. Synopsis Quine emphasizes his naturalism, the doctrine that philosophy should be pursued as part of natural science. He argues in favor of naturalizing epistemology, physicalism as against phenomenalism and mind-body dualism, and extensionality as against intensionality. He also develops a behavioristic conception of sentence-meaning, theorizes about language learning, speculates on the ontogenesis of reference, explains various forms of ambiguity and vagueness, and recommends measures for regimenting language so as to eliminate ambiguity and vagueness as well as to make a theory's logic and ontic co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Willard Van Orman Quine
Willard Van Orman Quine ( ; known to his friends as "Van"; June 25, 1908 – December 25, 2000) was an American philosopher and logician in the analytic tradition, recognized as "one of the most influential philosophers of the twentieth century". He was the Edgar Pierce Chair of Philosophy at Harvard University from 1956 to 1978. Quine was a teacher of logic and set theory. He was famous for his position that first-order logic is the only kind worthy of the name, and developed his own system of mathematics and set theory, known as New Foundations. In the philosophy of mathematics, he and his Harvard colleague Hilary Putnam developed the Quine–Putnam indispensability argument, an argument for the Philosophy of mathematics#Empiricism, reality of mathematical entities.Colyvan, Mark"Indispensability Arguments in the Philosophy of Mathematics" The Stanford Encyclopedia of Philosophy (Fall 2004 Edition), Edward N. Zalta (ed.). He was the main proponent of the view that philosophy is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |