|
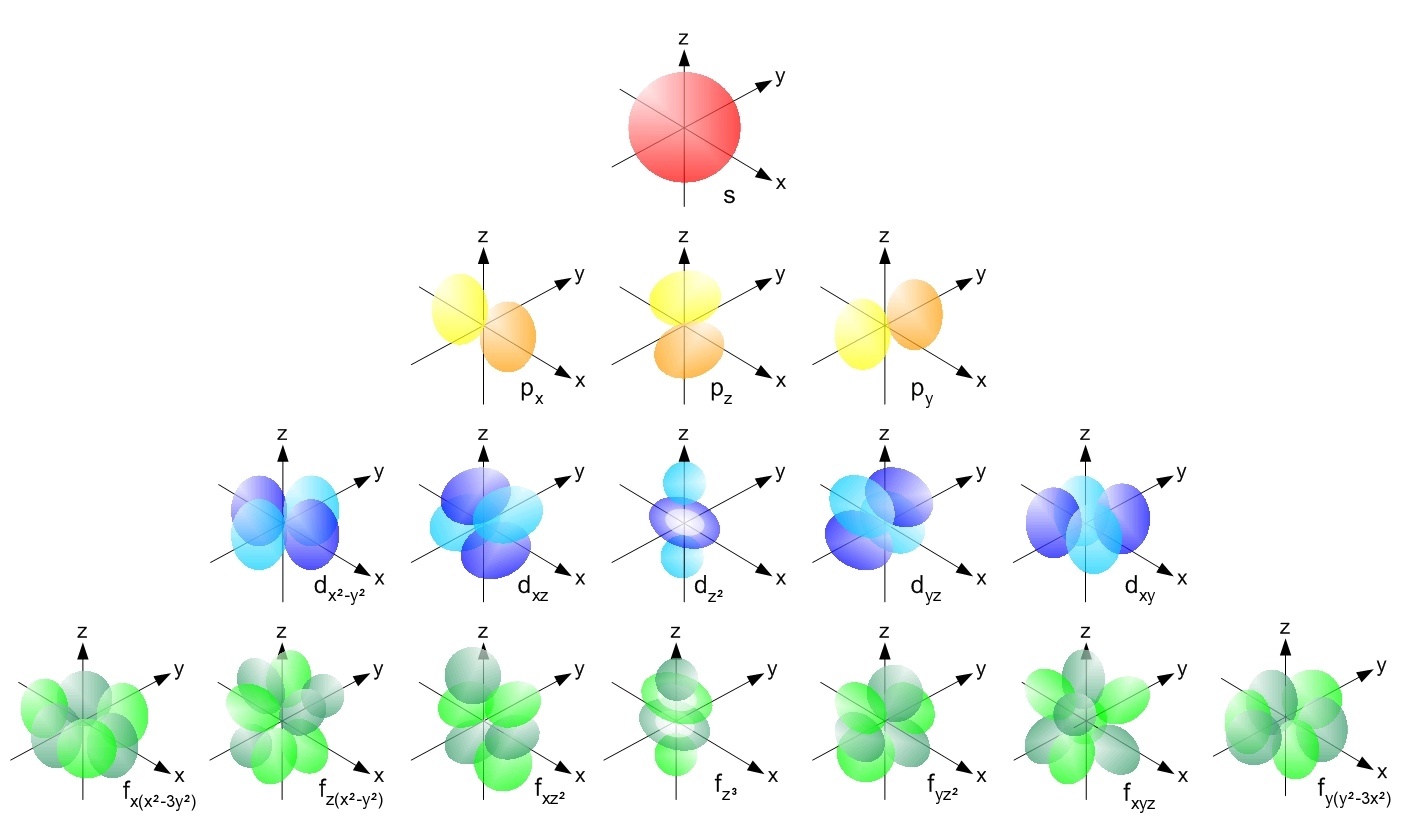
Orbital Motion (quantum)
Quantum orbital motion involves the quantum mechanical motion of rigid particles (such as electrons) about some other mass, or about themselves. In classical mechanics, an object's orbital motion is characterized by its orbital angular momentum (the angular momentum about the axis of rotation) and spin angular momentum, which is the object's angular momentum about its own center of mass. In quantum mechanics there are analogous orbital and spin angular momenta which describe the orbital motion of a particle, represented as quantum mechanical operators instead of vectors. The paradox of Heisenberg's Uncertainty Principle and the wavelike nature of subatomic particles make the exact motion of a particle impossible to represent using classical mechanics. The orbit of an electron about a nucleus is a prime example of quantum orbital motion. While the Bohr model describes the electron's motion as uniform circular motion, analogous to classical circular motion, in reality its location i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electrons
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up quark, up and down quark, down quarks. Electrons are extremely lightweight particles that orbit the positively charged atomic nucleus, nucleus of atoms. Their negative charge is balanced by the positive charge of protons in the nucleus, giving atoms their overall electric charge#Charge neutrality, neutral charge. Ordinary matter is composed of atoms, each consisting of a positively charged nucleus surrounded by a number of orbiting electrons equal to the number of protons. The configuration and energy levels of these orbiting electrons determine the chemical properties of an atom. Electrons are bound to the nucleus to different degrees. The outermost or valence electron, valence electrons are the least tightly bound and are responsible for th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Operator
Spin is an intrinsic form of angular momentum carried by elementary particles, and thus by composite particles such as hadrons, atomic nuclei, and atoms. Spin is quantized, and accurate models for the interaction with spin require relativistic quantum mechanics or quantum field theory. The existence of electron spin angular momentum is inferred from experiments, such as the Stern–Gerlach experiment, in which silver atoms were observed to possess two possible discrete angular momenta despite having no orbital angular momentum. The relativistic spin–statistics theorem connects electron spin quantization to the Pauli exclusion principle: observations of exclusion imply half-integer spin, and observations of half-integer spin imply exclusion. Spin is described mathematically as a vector for some particles such as photons, and as a spinor or bispinor for other particles such as electrons. Spinors and bispinors behave similarly to vectors: they have definite magnitudes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perturbation Theory
In mathematics and applied mathematics, perturbation theory comprises methods for finding an approximate solution to a problem, by starting from the exact solution of a related, simpler problem. A critical feature of the technique is a middle step that breaks the problem into "solvable" and "perturbative" parts. In regular perturbation theory, the solution is expressed as a power series in a small parameter The first term is the known solution to the solvable problem. Successive terms in the series at higher powers of \varepsilon usually become smaller. An approximate 'perturbation solution' is obtained by truncating the series, often keeping only the first two terms, the solution to the known problem and the 'first order' perturbation correction. Perturbation theory is used in a wide range of fields and reaches its most sophisticated and advanced forms in quantum field theory. Perturbation theory (quantum mechanics) describes the use of this method in quantum mechanics. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperfine Splitting
In atomic physics, hyperfine structure is defined by small shifts in otherwise degenerate electronic energy levels and the resulting splittings in those electronic energy levels of atoms, molecules, and ions, due to electromagnetic multipole interaction between the nucleus and electron clouds. In atoms, hyperfine structure arises from the energy of the nuclear magnetic dipole moment interacting with the magnetic field generated by the electrons and the energy of the nuclear electric quadrupole moment in the electric field gradient due to the distribution of charge within the atom. Molecular hyperfine structure is generally dominated by these two effects, but also includes the energy associated with the interaction between the magnetic moments associated with different magnetic nuclei in a molecule, as well as between the nuclear magnetic moments and the magnetic field generated by the rotation of the molecule. Hyperfine structure contrasts with ''fine structure'', which resul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lamb Shift
In physics, the Lamb shift, named after Willis Lamb, is an anomalous difference in energy between two electron orbitals in a hydrogen atom. The difference was not predicted by theory and it cannot be derived from the Dirac equation, which predicts identical energies. Hence the Lamb ''shift'' is a deviation from theory seen in the differing energies contained by the 2''S''1/2 and 2''P''1/2 orbitals of the hydrogen atom. The Lamb shift is caused by interactions between the virtual photons created through vacuum energy fluctuations and the electron as it moves around the hydrogen nucleus in each of these two orbitals. The Lamb shift has since played a significant role through vacuum energy fluctuations in theoretical prediction of Hawking radiation from black holes. This effect was first measured in 1947 in the Lamb–Retherford experiment on the hydrogen microwave spectrum and this measurement provided the stimulus for renormalization theory to handle the divergences. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeeman Effect
The Zeeman effect () is the splitting of a spectral line into several components in the presence of a static magnetic field. It is caused by the interaction of the magnetic field with the magnetic moment of the atomic electron associated with its Angular momentum, orbital motion and Spin (physics), spin; this interaction shifts some orbital energies more than others, resulting in the split spectrum. The effect is named after the Netherlands, Dutch physicist Pieter Zeeman, who discovered it in 1896 and received a Nobel Prize in Physics for this discovery. It is analogous to the Stark effect, the splitting of a spectral line into several components in the presence of an electric field. Also, similar to the Stark effect, transitions between different components have, in general, different intensities, with some being entirely forbidden (in the dipole approximation), as governed by the selection rules. Since the distance between the Zeeman sub-levels is a function of magnetic field ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fine Structure
In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to electron spin and relativistic corrections to the non-relativistic Schrödinger equation. It was first measured precisely for the hydrogen atom by Albert A. Michelson and Edward W. Morley in 1887, laying the basis for the theoretical treatment by Arnold Sommerfeld, introducing the fine-structure constant. Background Gross structure The ''gross structure'' of line spectra is the structure predicted by the quantum mechanics of non-relativistic electrons with no spin. For a hydrogenic atom, the gross structure energy levels only depend on the principal quantum number ''n''. However, a more accurate model takes into account relativistic and spin effects, which break the degeneracy of the energy levels and split the spectral lines. The scale of the fine structure splitting relative to the gross structure energies is on the order of (''Zα'')2, where ''Z'' is the atomic number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fine-structure Constant
In physics, the fine-structure constant, also known as the Sommerfeld constant, commonly denoted by (the Alpha, Greek letter ''alpha''), is a Dimensionless physical constant, fundamental physical constant that quantifies the strength of the electromagnetic interaction between elementary charged particles. It is a dimensionless quantity (dimensionless physical constant), independent of the system of units used, which is related to the strength of the coupling of an elementary charge ''e'' with the electromagnetic field, by the formula . Its numerical value is approximately , with a relative uncertainty of The constant was named by Arnold Sommerfeld, who introduced it in 1916 Equation 12a, ''"rund 7·" (about ...)'' when extending the Bohr model of the atom. quantified the gap in the fine structure of the spectral lines of the hydrogen atom, which had been measured precisely by Albert A. Michelson, Michelson and Edward W. Morley, Morley in 1887. Why the constant should have t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalues And Eigenvectors
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a constant factor \lambda when the linear transformation is applied to it: T\mathbf v=\lambda \mathbf v. The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor \lambda (possibly a negative or complex number). Geometrically, vectors are multi-dimensional quantities with magnitude and direction, often pictured as arrows. A linear transformation rotates, stretches, or shears the vectors upon which it acts. A linear transformation's eigenvectors are those vectors that are only stretched or shrunk, with neither rotation nor shear. The corresponding eigenvalue is the factor by which an eigenvector is stretched or shrunk. If the eigenvalue is negative, the eigenvector's direction is reversed. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrogen-like Atom
A hydrogen-like atom (or hydrogenic atom) is any atom or ion with a single valence electron. These atoms are isoelectronic with hydrogen. Examples of hydrogen-like atoms include, but are not limited to, hydrogen itself, all alkali metals such as Rb and Cs, singly ionized alkaline earth metals such as Ca+ and Sr+ and other ions such as He+, Li2+, and Be3+ and isotopes of any of the above. A hydrogen-like atom includes a positively charged core consisting of the atomic nucleus and any core electrons as well as a single valence electron. Because helium is common in the universe, the spectroscopy of singly ionized helium is important in EUV astronomy, for example, of DO white dwarf stars. The non-relativistic Schrödinger equation and relativistic Dirac equation for the hydrogen atom can be solved analytically, owing to the simplicity of the two-particle physical system. The one-electron wave function solutions are referred to as ''hydrogen-like atomic orbitals''. Hydrogen-li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Potential
Electric potential (also called the ''electric field potential'', potential drop, the electrostatic potential) is defined as electric potential energy per unit of electric charge. More precisely, electric potential is the amount of work (physics), work needed to move a test charge from a reference point to a specific point in a static electric field. The test charge used is small enough that disturbance to the field is unnoticeable, and its motion across the field is supposed to proceed with negligible acceleration, so as to avoid the test charge acquiring kinetic energy or producing radiation. By definition, the electric potential at the reference point is zero units. Typically, the reference point is Earth (electricity), earth or a point at infinity, although any point can be used. In classical electrostatics, the electrostatic field is a vector quantity expressed as the gradient of the electrostatic potential, which is a scalar (physics), scalar quantity denoted by or occasi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |