Orbital Motion (quantum)

Quantum orbital motion involves the quantum mechanical motion of rigid particles (such as 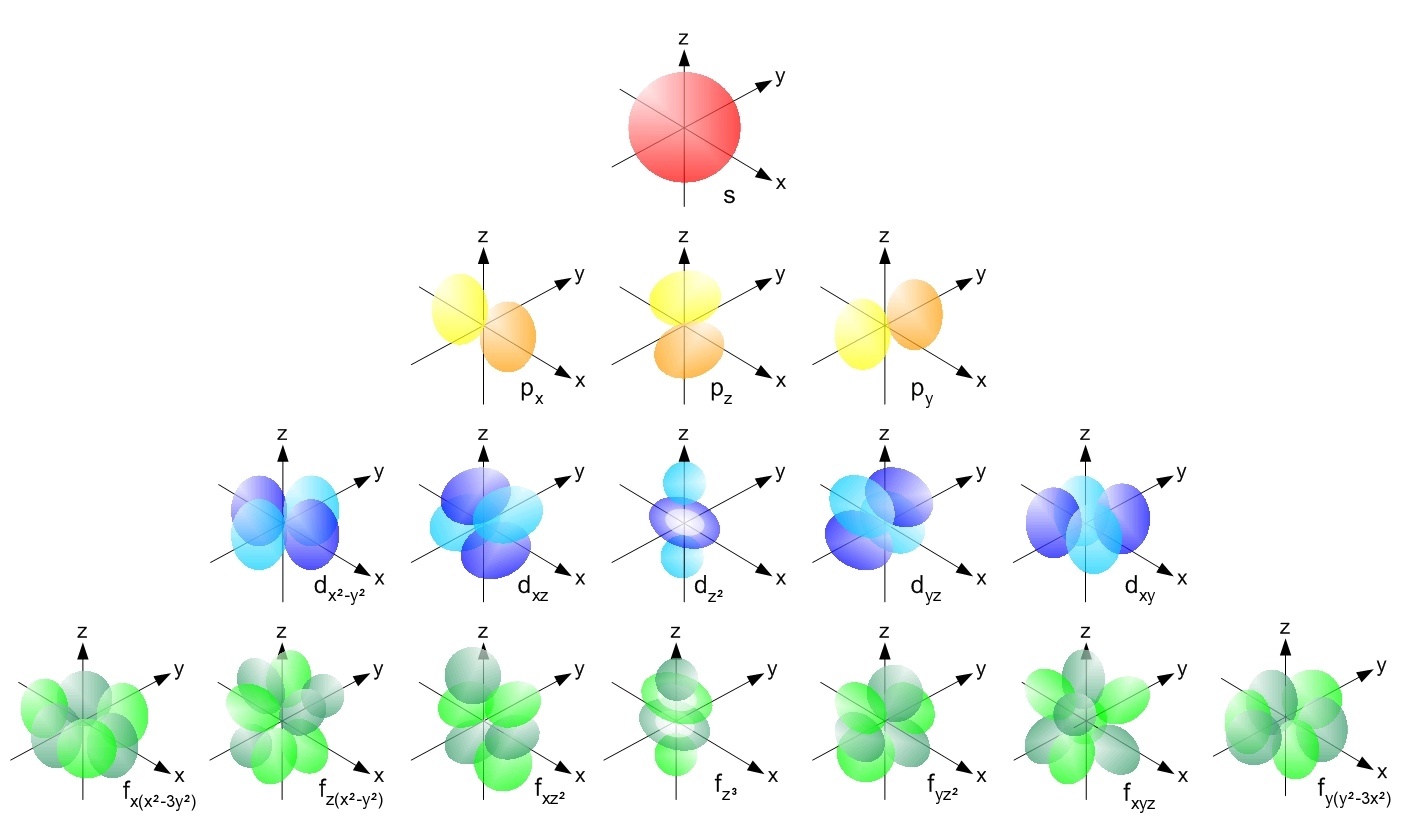electrons) about some other mass, or about themselves. In classical mechanics, an object's orbital motion is characterized by its orbital angular momentum (the angular momentum about the axis of rotation) and spin angular momentum, which is the object's angular momentum about its own center of mass. In quantum mechanics there are analogous orbital and spin angular momenta which describe the orbital motion of a particle, represented as quantum mechanical operators instead of vectors.

The paradox of Heisenberg's Uncertainty Principle and the wavelike nature of subatomic particles make the exact motion of a particle impossible to represent using classical mechanics. The orbit of an electron about a nucleus is a prime example of quantum orbital motion. While the Bohr model describes the electron's motion as uniform circular motion, analogous to classical circular motion, in reality its location in space is described by probability functions. Each probability function has a different average energy level, and corresponds to the likelihood of finding the electron in a specific atomic orbital, which are functions representing 3 dimensional regions around the nucleus. The description of orbital motion as probability functions for wavelike particles rather than the specific paths of orbiting bodies is the essential difference between quantum mechanical and classical orbital motion.

Orbital angular momentum

In quantum mechanics, the position of an electron in space is represented by its spatial wave function, and specified by three variables (as with x, y, and z Cartesian coordinates). The square of an electron's wave function at a given point in space is proportional to the probability of finding it at that point, and each wave function is associated with a particular energy. There are limited allowed wave functions, and thus limited allowed energies of particles in a quantum mechanical system; wave functions are solutions to Schrödinger's equation.

For hydrogen-like atoms, spatial wave function has the following representation:

$\psi_(r, \theta, \phi) = R_(r)Y_l^m(\theta, \phi)$

Electrons do not "orbit" the nucleus in the classical sense of angular momentum, however there is a quantum mechanical analog to the mathematical representation of L = r × p in classical mechanics. In quantum mechanics, these vectors are replaced by operators; the angular momentum operator is defined as the cross product of the position operator and the momentum operator, which is defined as $\hat = -i \hbar \nabla$.

Just as in classical mechanics, the law of conservation of angular momentum still holds.

Spin

An electron is considered to be a point charge.
The motion of this charge about the atomic nucleus produces a magnetic dipole moment that can be oriented in an external magnetic field, as with magnetic resonance. The classical analog to this phenomenon would be a charged particle moving around a circular loop, which constitutes a magnetic dipole. The magnetic moment and angular momentum of this particle would be proportional to each other by the constant $\gamma_0$, the gyromagnetic ratio. However, unlike bodies in classical mechanics an electron carries an intrinsic property called spin, which creates an additional (spin) magnetic moment.

The total angular momentum of a particle is the sum of both its orbital angular momentum and spin angular momentum.

A particle's spin is generally represented in terms of spin operators. It turns out for particles that make up ordinary matter (protons, neutrons, electrons, quarks, etc.) particles are of spin 1/2.
Only two energy levels (eigenvectors of the Hamiltonian) exist for a spin 1/2 state: "up" spin, or +1/2, and "down" spin, or -1/2.

Thus showing that the inherent quantum property of energy quantization is a direct result of electron spin.

Atomic orbitals

Using the formalisms of wave mechanics developed by physicist Erwin Schrödinger in 1926, each electron's distribution is described by a 3-dimensional standing wave. This was motivated by the work of 18th century mathematician Adrien Legendre.

The spatial distribution of an electron about a nucleus is represented by three quantum numbers: $n, l$ and $m_l$. These three numbers describe the electron's atomic orbital, which is the region of space occupied by the electron. Each set of these numbers constitutes a principal shell with a specific number of sub shells, each with a specific number of orbitals. Roughly speaking, the principle quantum number $n$ describes the average distance of an electron from the nucleus. The azimuthal quantum number $l$ describes the relative shape of the region of space (orbital) occupied by the electron. Finally, The magnetic quantum number $m_l$ describes the relative orientation of the orbital with respect to an applied magnetic field. The allowed values of $l$ and $m_l$ depend on the value of $n$.

Orbital motion of electrons in hydrogen-like atoms

The simplest physical model of electron behavior in an atom is an electron in hydrogen. For a particle to remain in orbit, it must be bound to its center of rotation by some radial electric potential. In this system, electrons orbiting an atomic nucleus are bound to the nucleus via the Coulomb potential, given by $V(r) = \frac \frac$. Classically, the energy of the electron orbiting a nucleus would be given as the sum of the kinetic and potential energies. The Bohr model of a hydrogen-like atom is a classical model of uniform circular motion. Its Hamiltonian is thus written in this way, as $H_ = \frac\nabla^2 - \frac\frac$. The first term is the kinetic energy of the electron (classically given as $\frac$, where in quantum mechanics we have replaced classical momentum $p$ with the momentum operator $p = -i\hbar\nabla$. The second term accounts for the Coulomb potential. The Bohr model energies, which are eigenvalues of the Bohr Hamiltonian, are of order $\alpha^2 mc^2$, where $\alpha$ is the unitless fine-structure constant, defined as $\alpha \equiv \frac \approx \frac$. (Since $\alpha$ is much less than 1, energy corrections with more factors of $\alpha$ are significantly smaller order shifts).

However, some revisions must be made to the simplified Bohr model of an electron in the hydrogen atom to account for quantum mechanical effects. These revisions to the electron's motion in a hydrogen atom are some of the most ubiquitous examples of quantum mechanical orbital motion. Ordered by greatest to smallest order of correction to the Bohr energies, the revisions are:

# Motion of the nucleus (of order $\alpha^4 mc^2$)
# Fine structure (of order $\alpha^4 mc^2$) or the Zeeman effect in the presence of a large magnetic field
## Relativistic correction
## Spin-orbit coupling
# Lamb shift (of order $\alpha^5 mc^2$): This is associated with the quantization of the electric field
# Hyperfine splitting (of order $\frac\alpha^4 mc^2$)
For each revision, the Hamiltonian is first rewritten, and then the shifted energy levels are calculated using perturbation theory.

Motion of the nucleus

The nucleus is not really perfectly stationary in space; the Coulomb potential attracts it to the electron with equal and opposite force as it exerts on the electron. However, the nucleus is far more massive than the orbiting electron, so its acceleration towards the electron is very small relative to the electron's acceleration towards it, allowing it to be modeled as a also This is accounted for by replacing the mass (m) in the Bohr Hamiltonian with the reduced mass ($\mu$) of the system.

Fine structure

# Relativistic correction: The first term in the Hamiltonian represents the kinetic energy of the electron in the atom. However, it comes from the classical expression for kinetic energy $T = \frac$. However despite the fact that the electron is moving at relativistic speeds. The relativistic kinetic energy is given as the difference between the electron's total kinetic energy and its rest energy, $T = \frac - mc^2$. Expressing T in terms of the relativistic momentum of the electron and Taylor expanding in powers of the small number $\frac$, yields a new expression for the kinetic energy which reduces to the classical term to first order: $T = \frac - \frac + ...$. Giving the lowest-order correction to the Hamiltonian as $H_r ^\prime = - \frac$. In non-denerate perturbation theory, the first order correction to energy levels is given by the expectation value of $H ^\prime$ in the unperturbed state. $E_r^1 = \langle \psi , H_r^\prime, \psi \rangle$, and for the unperturbed states the Schrödinger equation reads $p^2\psi = 2m(E-v)\psi$. Putting these together, the correction to energy is E_r^1 = - \frac ^2 - 2E \langle V\rangle + \langle V^2\rangle/math>. Substituting in the Coulomb potential and simplifying, we get $E_r^1 = - \frac \lbrack\frac -3\rbrack$.
# Spin-orbit coupling: Each spin-1/2 electron behaves like a magnetic moment; the presence of a magnetic field exerts a torque which tends to align its magnetic moment $\mu$ with the direction of the field. From the reference frame of the electron, the proton is circling around it; this orbiting positive charge creates a magnetic field B in its frame. Relativistic calculations give the magnetic moment of the electron as $\vec\mu_e = -\frac\vec S$, where S is the spin of the electron. The Hamiltonian for a magnetic moment is given as $H = -\vec\mu \cdot \vec B$The magnetic field from the proton can be derived from the Biot-Savart law, picturing the proton as a continuous current loop from the perspective of the electron: $\vec B = \frac\frac\vec L$. With an extra factor of 1/2 to account for Thomas precession, which accounts for the fact that the frame of the electron is non-inertial, the Hamiltonian is $H_^\prime = (\frac)\frac\vec S \cdot \vec L$. After some calculation of the eigenvalues of $\vec S\cdot \vec L$, the energy levels are found to be$E_^1 = \frac\frac$.

After accounting for all fine structure, the energy levels of the hydrogen-like atom are labeled as: $E_^1 = \frac[1 + \frac(\frac- \frac )\rbrack$

The Zeeman effect

When an atom is placed in a uniform external magnetic field B, the energy levels are shifted. This phenomenon shifts the Hamiltonian with the factor $H_z^\prime = \frac(\vec L+2 \vec S) \cdot \vec B_$, where L is the electron's angular momentum and S is its spin.

In the presence of a weak magnetic field, the fine structure dominates and the Zeeman Hamiltonian term is treated as the perturbation to the unperturbed Hamiltonian, which is a sum of the Bohr and fine structure Hamiltonians. The Zeeman corrections to the energy are found to be $E_z^1 = \mu_B g_J B_ m_j$, where $\mu_B\equiv \frac = 5.788\times 10^-5 eV/T$, is the Bohr magneton.

In a strong magnetic field, the Zeeman effect dominates and the unperturbed Hamiltonian is taken to be $H_+ H_Z^\prime$, with the correction $H_^\prime$. The corrected energy levels are labeled as: $E_^1 = \frac\alpha^2\lbrack \frac - (\frac)\rbrack$.

Hyperfine splitting

The proton also constitutes a weak magnetic dipole, and hyperfine splitting describes the effect is due to the interaction between the magnetic dipole moments of the electron and the proton. This effect gives rise to energy level shifts $E_\text^1 = \frac\langle \vec S_p \cdot \vec S_e\rangle$. It is called spin–spin coupling because it involves the dot product between the spins of the electron and the proton.

Applications

The Einstein-de Haas effect describes the phenomena in which a change in this magnetic moment causes the electron to rotate. Similarly, the Barnett effect describes the magnetization of the electron resulting from being spun on its axis. Both of these effects demonstrate the close tie between classical and quantum mechanical orbital motion.

See also

*Atomic orbital
* Electron orbital
*Electron
*Lorentz-violating neutrino oscillations
*Orbital magnetization

References

{{Reflist

External links

Primer on Quantum Theory of the Atom

Magnetism